Polynomifunktiot
Luvun tavoitteet
Tämän luvun tavoitteena on, että sievennät sujuvasti polynomilausekkeita. Osaat
- määrittää polynomin asteluvun ja vakiotermin
- laskea polynomien summan ja erotuksen
- laskea polynomien tulon
- sieventää polynomilausekkeita teknisen apuvälineen avulla
- tutkia polynomifunktioita teknisen apuvälineen avulla.
Polynomien laskutoimituksia
Tässä kappaleessa palautetaan mieleen, miten polynomeilla lasketaan. Polynomi tarkoittaa lauseketta, joka on muodostettu muuttujista (eli kirjaimista) ja vakioista (eli luvuista) käyttämällä yhteen-, vähennys- ja kertolaskua. Esimerkiksi $$2x^3-5x^2 + 8x -3$$ on polynomi, samoin $$7x^4-9.$$ Polynomissa voi olla myös useampia muuttujia. Esimerkiksi $$5xy^2-3x+5y^3-3$$ on kahden muuttujan polynomi. Tässä moduulissa keskitytään yhden muuttujan polynomeihin.
Polynomit
Mitkä seuraavista väitteistä ovat oikein? Perustele vastauksesi omin sanoin ja korjaa samalla väärät väitteet oikeiksi. Kertaa tarvittaessa polynomeihin liittyviä käsitteitä Opetus.tv:n sivuilta.
- Polynomissa $-4x^2+8x-3$ on viisi termiä.
- Polynomin $7x^4-6x^3+4x$ toisen asteen termin kerroin on nolla.
- Polynomin $x^7-x+6$ aste on kolme.
- Polynomin $x^3-9x^2+4$ vakiotermi on $4$.
- Polynomi $3x^5-x^2$ on monomi.
- Lauseke $\dfrac{x^2}{4}-\dfrac{x}{2}$ on binomi.
Vastaus
- Väärin, polynomissa on kolme termiä.
- Oikein, sillä sama polynomi voidaan kirjoittaa $7x^4-6x^3 + 0x^2 +4x$.
- Väärin, polynomin aste on 7.
- Oikein.
- Väärin, tämä polynomi on binomi. Monomiksi sanotaan polynomia, jossa on vain yksi termi.
- Oikein, sillä tämä lauseke voidaan kirjoittaa muodossa $\frac{1}{4}x^2 - \frac{1}{2}x$.
Polynomien yhteen- ja vähennyslaskussa yhdistetään samaa astetta olevat termit. Seuraavat laskut havainnollistavat ideaa:
Reppureissaaja löytää lompakostaan 35 euroa ja 25 puntaa. Hänen kaverillaan on puolestaan taskussaan 15 euroa ja 7 puntaa. Kuinka paljon rahaa kaveruksilla on yhteensä? \begin{align*} &\quad (35 \,€ + 25 \,£) + (15 \,€ + 7 \,£) \\ &= 50 \,€ + 32 \,£. \end{align*} Tässä laskettiin eurot yhteen keskenään ja punnat yhteen keskenään. Yhdistettiin siis ne luvut, joilla kirjainosa oli sama.
Paluumatkalla kaverukset ostavat tuliaisia ja käyvät syömässä. Tähän kuluu yhteensä 40 euroa ja 27 puntaa. Kuinka paljon rahaa jää jäljelle? \begin{align*} &\quad (50 \,€ + 32 \,£) \textcolor{red}{-} (40 \,€ + 27 \,£) \\ &= 50 \,€ + 32 \,£ \textcolor{red}{-} 40 \,€ \textcolor{red}{-} 27 \,£\\ &= 10 \,€ + 5 \,£. \end{align*} Huomaa, että polynomien vähennyslaskussa jälkimmäisen polynomin jokainen merkki vaihtuu.
Polynomien yhteen- ja vähennyslasku
Muodosta ja laske polynomien $x^2+3x-6$ ja $-4x^2+x-2$
- summa
- erotus.
Vastaus
- $-3x^2+4x-8$
- $5x^2+2x-4$
Polynomien yhteen- ja vähennyslasku
Muodosta ja laske polynomien $4x^3-2x^2+3x+1$ ja $-3x^2-3x+2$
- summa
- erotus.
Vastaus
- $4x^3-5x^2+3$
- $4x^3+x^2+6x-1$
Kun polynomia kerrotaan luvulla, kerrotaan jokainen polynomin termi erikseen samaan tapaan kuin seuraavassa laskussa:
Kun reppureissaaja ja hänen kaverinsa palasivat Suomeen, he päättivät lahjoittaa viidesosan jäljelle jääneistä rahoista hyväntekeväisyyteen ja jakaa loput rahoista tasan. Kuinka paljon he lahjoittivat hyväntekeväisyyteen? \begin{align*} \frac{1}{5} (10 \,€ + 5 \,£) &= \frac{1}{5} \cdot 10 \,€ + \frac{1}{5} \cdot 5 \,£\\[1mm] &= \frac{10}{5} \,€ + \frac{5}{5} \,£\\[1mm] &= 2 \,€ + 1 \,£ \end{align*} Jos molemmissa tulon tekijöissä on kirjainosa, sievennetään lopputuloksen kirjainosa potenssin määritelmän ja laskusääntöjen mukaan. Esimerkiksi monomien $-2x^3$ ja $-4x^2$ tulo on \begin{align*} -2x^3\cdot (-4x^2) &= -2 \cdot (-4) \cdot xxxxx \\ &= 8x^5 \end{align*}
Monomin ja polynomin tulo
Laske seuraavat tulot:
- $-3x^4 \cdot 5x^2$
- $4x(x-5)$
- $-3x^2(-4x^2+x-2)$
Vastaus
- $-15x^6$
- $4x^2-20x$
- $12x^4 - 3x^3 + 6x^2$
Samalla tavalla toimiaan myös silloin, kun polynomi kerrotaan monomilla: $$ \textcolor{blue}{2x}(3x-4) = \textcolor{blue}{2x} \cdot 3x - \textcolor{blue}{2x}\cdot 4 = 6x^2 - 8x. $$
Kahden polynomin tulo lasketaan vaiheittain: otetaan ensimmäisen tulon tekijän
- ensimmäinen termi ja kerrotaan sillä toisen tulon tekijän jokainen termi erikseen
- toinen termi ja kerrotaan sillä toisen tulon tekijän jokainen termi erikseen
- kolmas termi ja kerrotaan sillä toisen tulon tekijän jokainen termi erikseen.
Näin jatketaan, kunnes ensimmäisen tulon tekijän kaikki termit on käytetty. Esimerkiksi tulossa $$(2x-5)(3x-4)$$ kerrotaan jälkimmäisen polynomin kaikki termit ensin monomilla $2x$ ja sen jälkeen monomilla $-5$: \begin{align*} (\textcolor{blue}{2x}\textcolor{red}{-5})(3x-4) &= \textcolor{blue}{2x} \cdot 3x - \textcolor{blue}{2x} \cdot 4 + (\textcolor{red}{-5}) \cdot 3x + (\textcolor{red}{-5}) \cdot (-4) \\ &= \textcolor{blue}{6x^2 - 8x}\textcolor{red}{-15x + 20} \\ &= 6x^2 - 23x + 20 \end{align*}
Polynomien tulo
Laske seuraavat tulot:
- $x(7-5x)$
- $(x+2)(8x-1)$
- $(4x+3)(4x-3)$
- Tarkista edelliset kohdat TI Nspirellä kirjoittamalla laskinohjelmaan expand(lauseke), esim. a-kohdassa kirjoita expand(x(7-5x)).
Vastaus
- $x(7-5x) = 7x-5x^2$
- $(x+2)(8x-1) = 8x^2 + 15x - 2$
- $(4x+3)(4x-3) = 16x^2 - 9$
Polynomien potenssit voidaan laskea muuttamalla ne ensin tulomuotoon. Esimerkiksi \begin{align*} (x-5)^2 &= (x-5)(x-5) \\[1mm] &= x^2 - 5x - 5x + 25 \\[1mm] &= x^2 - 10x + 25. \end{align*}
Polynomien potenssi
Laske seuraavat potenssit. Aloita kirjoittamalla lauseke tulomuodossa.
- $(x+3)^2$
- $(2x-1)^2$
- $(7-x)^2$
Vastaus
- $(x+3)^2 = x^2 + 6x + 9$
- $(2x-1)^2 = 4x^2 - 4x + 1$
- $(7-x)^2 = 49 - 14x + x^2$
Polynomifunktio teknisen apuvälineen avulla
Lopuksi harjoitellaan teknisen apuvälineen käyttämistä polynomifunktioiden tutkimisessa.
Teknisen apuvälineen käyttö polynomifunktioiden tutkimisessa
Tehtävänä on harjoitella teknisen apuvälineen käyttöä polynomifunktioiden tutkimisessa.
- Avaa TI Nspire ja määrittele laskimeen funktio kirjoittamalla `f(x):=3x^2-2x+1` ja paina enter.
- Testaa, että funktio on laskimessa muistissa ja laske funktion arvo kohdassa $x=2$ kirjoittamalla `f(2)` ja paina enter. Saitko vastaukseksi 9?
- Jaa näyttö ylävalikosta kahteen osaan ja valitse toiseksi sovellukseksi Kuvaajat. Kirjoita `f1(x)=` kohdan perään `f(x)` ja paina enter. Funktion lauseke on edelleen laskimen muistissa, joten funktion kuvaajan pitäisi tulla näkyviin heti. Voit toki näpytellä funktion lausekkeen uudelleen, jos haluat.
- Jos tuntui hankalalta, niin katso [video](https://watch.screencastify.com/v/ccgKCJmkMtL9AYCIMzfr), jossa tehtiin tämä sama tehtävä ja yritä sitten uudelleen.
Polynomifunktio teknisen apuvälineen avulla
Eräässä matematiikan kokeessa arvosanoja kuvasi funktio $f(x)=\frac{5}{42}x+\frac{110}{42}$, missä $x$ oli kokeesta saatu pistemäärä. Ratkaise tehtävä laskinohjelmiston avulla.
- Laske funktion lausekkeen avulla, minkä arvosanan kokeesta sai 40 pisteellä.
- Ratkaise funktion kuvaajan avulla, millä pistemäärällä sai arvosanan 5.
- Arvioi kuvaajan perusteella, mikä oli kokeen maksimipistemäärä. Perustele.
VASTAUS
- $f(40)=7,38…\approx 7$ eli kokeesta sai arvosanan 7.
- Lukemalla kuvaajasta, mikä on $x$, kun $y=5$, huomataan, että pistemäärä oli 20.
- Katsotaan kuvaajasta, mikä on $x$, kun $y=10$. Huomataan, että arvosanan 10 on saanut pistemäärällä 62, joten maksimipistemäärä on voinut olla noin 70.
TEHTÄVÄSARJA II
Polynomien laskutoimituksia
Sievennä seuraavat lausekkeet:
- $(2x + 4) + (3x-8)$
- $(x - 7) - (2x - 2)$
- $x + 5x^2 - 3x^2 + 3x - x^2$
Vastaus
- $5x - 4$
- $-x-5$
- $4x + x^2$
Polynomien laskutoimituksia
Sievennä seuraavat lausekkeet:
- $7 - 3(4x-2)$
- $2(5y + 4) + 2(y + 9)$
- $3(x - 2x^2)-(x + x^2) + 2(x + 3x^2)$
Vastaus
- $-12x + 13$
- $12y + 26$
- $4x - x^2$
Polynomien laskutoimituksia
Sievennä seuraavat lausekkeet:
- $5x(x-3)$
- $-4x^2(8x-7x^3)$
- $6a(1-9b)$
Vastaus
- $5x^2 - 15x$
- $-32x^3 + 28x^5$
- $6a - 54ab$
Murtolausekkeiden sieventäminen
Sellaiset murtolausekkeet, joiden osoittajana on polynomi ja nimittäjänä jokin luku, ovat itsekin polynomeja. Esimerkiksi murtolauseketta \begin{align*} \frac{x-2}{5} \end{align*} voidaan muokata tekemällä jakolasku termeittäin seuraavasti: \begin{align*} \frac{x-5}{4} &= \dfrac{x}{4}-\dfrac{5}{4} = \frac{1}{4}x - \frac{5}{4} \end{align*} Huomaa, että neljällä jakaminen vastaa yhdellä neljäsosalla kertomista. Viimeisestä muodosta nähdään, että kysymyksessä on ensimmäisen asteen polynomi.
Muokkaa murtolauseke polynomiksi tekemällä jakolasku termeittäin:
- $\dfrac{15x - 3}{5}$
- $\dfrac{4x + 6}{12}$
Vastaus
- Tehdään jakolasku termeittäin: \begin{align*} \dfrac{15x - 3}{5} &= \dfrac{15x}{5} - \dfrac{3}{5} \\[1mm] &= 3x - \dfrac{3}{5} \end{align*}
- Tehdään jakolasku termeittäin ja supistetaan: \begin{align*} \dfrac{4x + 6}{12} &= \dfrac{4x}{12} + \dfrac{6}{12} \\[1mm] &= \dfrac{x}{3} + \dfrac{1}{2} \\[1mm] &= \dfrac{1}{3}x + \dfrac{1}{2} \end{align*}
Murtolausekkeen sieventäminen
Kun lasketaan murtolausekkeena kirjoitettujen polynomien summia ja erotuksia, pitää lausekkeet laventaa samannimisiksi samaan tapaan kuin murtoluvuilla laskettaessa. Lisäksi pitää huomata, että miinusmerkki murtolausekkeen edessä vaikuttaa koko osoittajaan. Esimerkiksi \begin{align*} \frac{5x-7}{2}\textcolor{red}{-}\frac{x-4}{3} &= \frac{\textcolor{blue}{3}(5x-7)}{\textcolor{blue}{3} \cdot 2}\textcolor{red}{-}\frac{\textcolor{blue}{2}(x-4)}{\textcolor{blue}{2} \cdot 3} \\[1mm] &= \frac{3(5x-7)}{6}\textcolor{red}{-}\frac{2(x-4)}{6} \\[1mm] &= \frac{3(5x-7)\textcolor{red}{-}2(x-4)}{6} \\[1mm] &= \frac{15x-21\textcolor{red}{-}2x\textcolor{red}{+}8}{6} \\[1mm] &= \frac{13x-13}{6} \\[1mm] &= \frac{13}{6}x - \frac{13}{6} \end{align*}
Sievennä seuraavat lausekkeet.
- $\dfrac{8x-11}{3} + \dfrac{4x - 7}{3}$
- $\dfrac{7-5x}{8} - \dfrac{3x - 5}{8}$
- $\dfrac{3x+1}{2} + \dfrac{x-4}{5}$
- $\dfrac{3x+1}{2} - \dfrac{x-4}{5}$
Vastaus
- \begin{align*} \dfrac{8x-11 + 4x - 7}{3} &= \dfrac{12x - 18}{3} \\[1mm] &= 4x - 6 \end{align*}
- \begin{align*} \dfrac{7-5x-(3x-5)}{8} &= \dfrac{7-5x-3x+5}{8} \\[1mm] &= \dfrac{12-8x}{8} \\[1mm] &= \dfrac{12}{8} - \dfrac{8x}{8} \\[1mm] &= \dfrac{3}{2} - x \end{align*}
- $\dfrac{17x-3}{10} = \dfrac{17}{10}x - \dfrac{3}{10}$
- $\dfrac{13x+13}{10} = \dfrac{13}{10}x + \dfrac{13}{10}$
Polynomien tulo
Sievennä seuraavat lausekkeet:
- $(3x+1)(3x-1)$
- $(4x+5)^2$
- $(6x-2)^2$
Vastaus
- $9x^2-1$
- $16x^2+40x+25$
- $36x^2-24x+4$
Polynomien tulo
Sievennä seuraavat lausekkeet:
- $(x+2)(x^2-5x+4)$
- $3x(x-6) - (x-2)(x-4)$
- $\left(\dfrac{x}{2} + 1\right)\left(8x + \dfrac{1}{4}\right)$
Vastaus
- $x^3 - 3x^2 - 6x + 8$
- $2x^2-12x-8$
- $4x^2+ \dfrac{65}{8}x+\dfrac{1}{4}$
Polynomien laskutoimituksia
Muokkaa murtolauseke polynomiksi tekemällä jakolasku termeittäin:
- $\dfrac{15x + 10}{5}$
- $\dfrac{20x^2 + 8x}{2x}$
- $\dfrac{14x^4 + 7x^2}{7x^2}$
Vastaus
- $3x + 2$
- $10x + 4$
- $2x^2 + 1$
Polynomien laskutoimituksia
Laske:
- $\dfrac{3x + 3}{4} - \dfrac{5x-1}{12}$
- $\dfrac{x}{3} - \dfrac{2-x}{4}$
- $x - \dfrac{2(x-1)}{5}$
Vastaus
- $\dfrac{1}{3}x + \dfrac{5}{6}$
- $\dfrac{7}{12}x - \dfrac{1}{2}$
- $\dfrac{3}{5}x + \dfrac{2}{5}$
Polynomien laskutoimituksia
TaksiTapsalla matkan hinnan riippuvuutta kuljetusta matkasta kuvastaa funktio $t(x)=1,84x+5,30$. AutoAinolla vastaava funktio on $a(x)=2x+3,90$. Molemmissa funktioissa hinnan yksikkönä on euro ja matkan yksikkönä kilometri.
- Laske funktion lausekkeen avulla, kuinka paljon TaksiTapsalla maksaa matkustaa 25 kilometriä.
- Tulkitse funktion lausekkeen avulla, mikä on taksimatkan aloitusmaksu TaksaTapsalla. Entä AutoAinolla?
- Piirrä teknisellä apuvälineellä molempien funktioiden kuvaajat samaan kuvaan. Selvitä kuvan avulla, millä matkan pituudella molemmat taksifirmat ovat yhtä kalliita. Millaisilla matkoilla kannattaa valita TaksiTapsa? Entä AutoAino? Muista selittää sanallisesti, miten tulkitsit vastaukset kuvasta.
Vastaus
- $t(25)=51,30$, eli 51,30 euroa
- Aloitusmaksu vastaa tilannetta $x=0$, eli lausekkeen vakiotermi kertoo aloitusmaksun. Näin ollen esimerkiksi TaksiTapsalla se on 5,30 euroa.
- Yhtä kalliit matkat löytyvät kuvaajien leikkauspisteestä. Siitä pienemmillä $x$:llä alempana oleva kuvaaja on halvempi ja vastaavasti tämä on sitten kalliimpi leikkauspisteen jälkeen.
Polynomifunktion sovellukset
Suorakulmion kannan pituus on $2x+7$. Suorakulmion korkeus on 3 yksikköä lyhyempi kuin kanta. Voit tarvittaessa tarkistaa Maolista, millainen suorakulmio on ja miten lasketaan suorakulmion piiri ja pinta-ala.
- Ilmaise suorakulmion korkeus muuttujan $x$ avulla sanottuna.
- Muodosta lauseke, joka kuvaa suorakulmion piiriä. Toisin sanoen, ilmaise suorakulmion piiri muuttujan $x$ avulla. Sievennä lauseke.
- Muodosta lauseke, joka kuvaa suorakulmion pinta-alaa. Sievennä lauseke.
- Laske suorakulmion piiri ja pinta-ala, kun $x=4$.
Vastaus
- $(2x+7)-3=2x+4$
- $8x+22$
- $4x^2+22x+28$
- Piiri on 54 ja pinta-ala on 180.
Polynomifunktion sovellukset
Suorakulmion kannan pituus on $2x+7$. Suorakulmion korkeus on 3 yksikköä lyhyempi kuin kanta. Voit tarvittaessa tarkistaa Maolista, millainen suorakulmio on ja miten lasketaan suorakulmion piiri ja pinta-ala.
- Ilmaise suorakulmion korkeus muuttujan $x$ avulla sanottuna.
- Muodosta lauseke, joka kuvaa suorakulmion piiriä. Toisin sanoen, ilmaise suorakulmion piiri muuttujan $x$ avulla. Sievennä lauseke.
- Muodosta lauseke, joka kuvaa suorakulmion pinta-alaa. Sievennä lauseke.
- Laske suorakulmion piiri ja pinta-ala, kun $x=4$.
Vastaus
- $(2x+7)-3=2x+4$
- $8x+22$
- $4x^2+22x+28$
- Piiri on 54 ja pinta-ala on 180.
Kevään 2015 ylioppilaskokeen tehtävä 3
Erään mallin mukaan naisten kuntoharjoittelun maksimisyke lasketaan kaavalla $226-T$ ja miesten maksimisyke kaavalla $220-T$ , kun $T$ on henkilön ikä vuosina.
- Kuinka monta prosenttia 18‐vuotiaan naisen maksimisyke on samanikäisen miehen maksimisykettä korkeampi?
- Erään suosituksen mukaan kuntoharjoittelussa sykkeen tulisi olla 60−70 % maksimisykkeestä. Määritä nämä rajat 30‐vuotiaalle naiselle.
Vastaus
Syksyn 2012 ylioppilaskokeen tehtävä 11
Aikuisen ihmisen sääriluun pituus $y$ riippuu henkilön pituudesta $x$ kaavojen \begin{align*} y &= 0,43x - 27 \textrm{(nainen)}\\ y &= 0,45x - 31 \textrm{(mies)}\\ \end{align*} mukaisesti, kun yksikkönä on senttimetri.
- Arkeologi löytää naisen sääriluun, joka on 41 cm pitkä. Kuinka pitkä nainen oli?
- Kaivauksissa löytyneen miehen pituudeksi arvioidaan 175 cm. Miehen läheltä löytyy sääriluu, jonka pituus on 42 cm. Onko kyseessä saman henkilön sääriluu?

`\
Korkeamman asteen polynomifunktio
Alla on näkyvissä polynomifunktioiden kuvaajia. Täydennä alla oleva taulukko kirjaamalla näkyviin funktioiden asteluvut ja yhdistämällä jokainen kuvaaja oikeaan funktioon.
| Funktio | Aste | Kuvaaja |
|---|---|---|
| $f(x) = -\frac{1}{10}x^5+x^3+1$ | ||
| $g(x) = -\frac{1}{2}x^4+\frac{3}{2}x^3 + \frac{3}{2}x^2-4x+2$ | ||
| $h(x) = x^4+x^3-3x^2-3x$ | ||
| $k(x) = \frac{1}{5}x^3-2x-1$ |
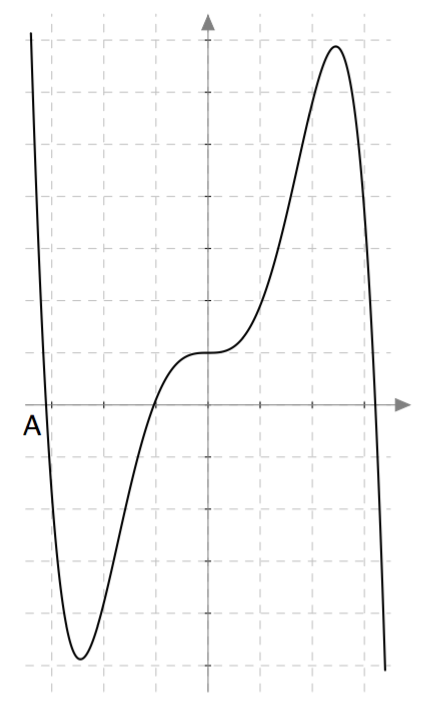
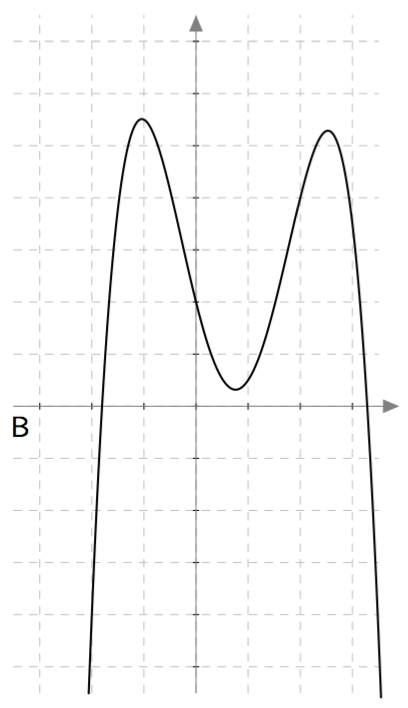
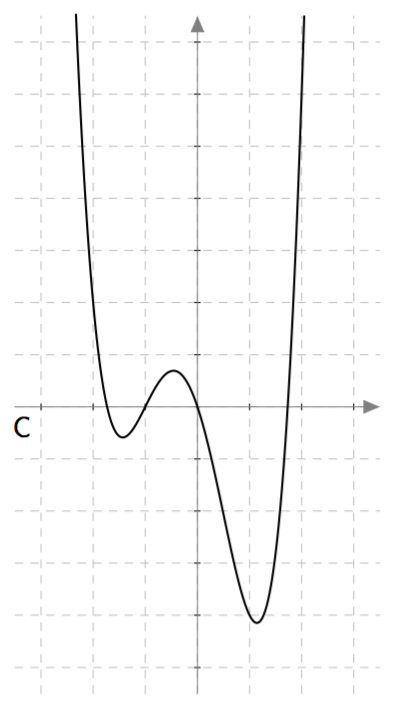
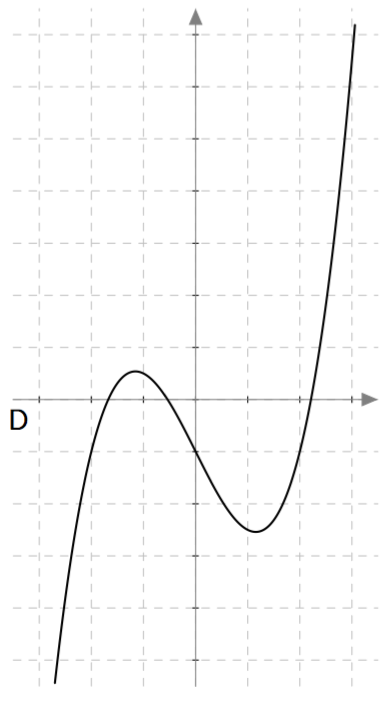
Vihje: Laske funktion arvo kohdassa $x=0$.
Vastaus
| Funktio | Aste | Kuvaaja |
|---|---|---|
| $\ f(x) = -\frac{1}{10}x^5+x^3+1 \ $ | 5 | A |
| $\ g(x) = -\frac{1}{2}x^4+\frac{3}{2}x^3 + \frac{3}{2}x^2-4x+2\ $ | 4 | B |
| $\ h(x) = x^4+x^3-3x^2-3x\ $ | 4 | C |
| $\ k(x) = \frac{1}{5}x^3-2x-1\ $ | 3 | D |
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä seuraavat tehtävät.
1. Ratkaise A-osan tapaan ja kirjoita ratkaisu Abitin editorilla osoitteessa kaava.mafynetti.fi.
- Muodosta ja laske polynomien $x^2+2x$ ja $2x-1$ erotus.
- Sievennä $3x(2x^2-5)$.
2. Ratkaise B-osan tapaan ja kirjoita ratkaisu TI Nspiren Muistiinpanot -sovelluksella.
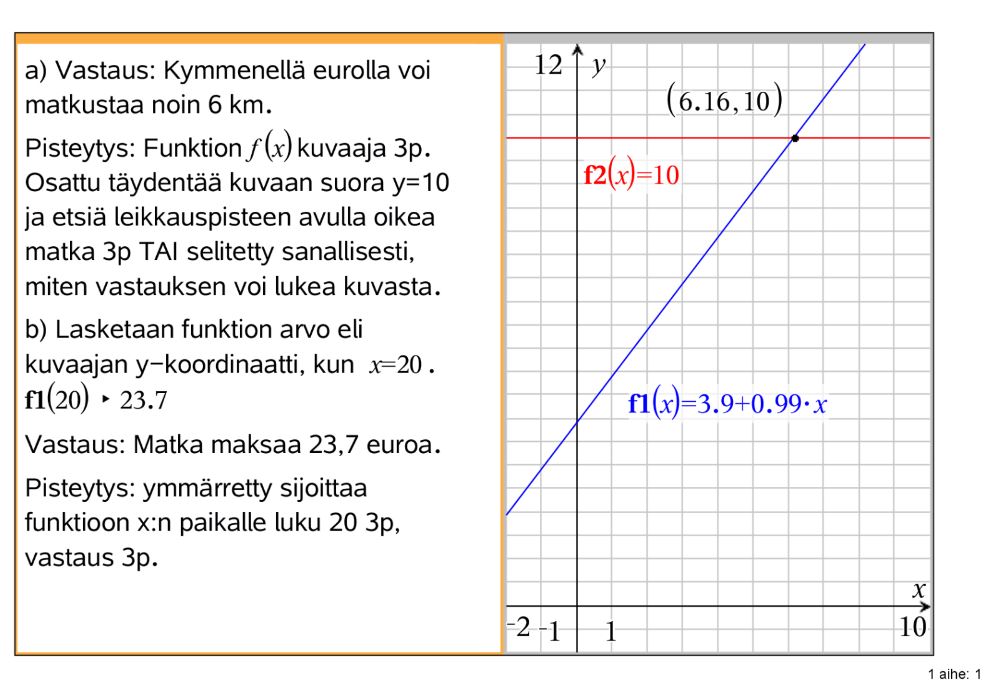
Taksimatkan hintaa kuvaa funktio $f(x)=3,90+0,99x$, missä $x$ on ajettujen kilometrien määrä.
- Ratkaise graafisesti, kuinka monta kilometriä voi ajaa 10 eurolla.
- Ratkaise algebrallisesti, kuinka paljon maksaa 20 kilometrin matka taksilla.
Vastaus
1.
- $(x^2+2x)-(2x-1)=x^2+2x-2x+1=x^2+1$
- $3x(2x^2-5)=3x\cdot 2x^2+3x\cdot (-5)=6x^3-15x$
Pisteytysohje:
- Polynomien erotus 2p, sulkujen poistaminen 2p, samanmuotoisten termien yhdistäminen 2p.
- Jokin järkevä aloitus 2p, termi $6x^3$ oikein 2p, termi $-15x$ oikein 2p.
2.