Raja-arvot ja jatkuvuus
Luvun tavoitteet
Tämän luvun tavoitteena on, että hahmotat funktion raja-arvon ja jatkuvuuden käsitteet visuaalisesti ja tunnistat funktion kuvaajasta kohdat, joissa funktiolla ei ole derivaattaa. Osaat
- päätellä funktion kuvaajan avulla,
- onko funktiolla tietyssä kohdassa raja-arvo
- onko funktio tietyssä kohdassa jatkuva
- onko funktio tietyssä kohdassa derivoituva
- määrittää funktion raja-arvon sekä laskemalla että kuvaajan avulla
- soveltaa Bolzanon lausetta funktion nollakohtien tutkimiseen ja polynomiyhtälöiden ratkaisemiseen.
Funktion raja-arvo
Tarkastellaan alla olevaa funktion $f$ kuvaajaa. Havaitaan, että funktio $f$ on määritelty kohdan $x = 1$ läheisyydessä sen molemmilla puolilla, mutta ei kohdassa $x = 1$.
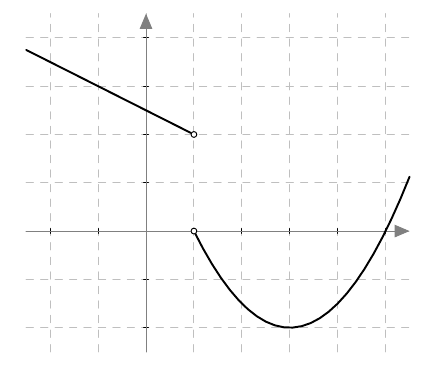
Tutkitaan funktion $f$ arvoja kohdan $x = 1$ eri puolilla. Huomataan, että funktion $f$ arvot lähestyvät lukua 2, kun lähestytään kohtaa $x = 1$ vasemmalta. Jos kohtaa $x = 1$ lähestytään oikelta, funktion $f$ arvot lähestyvät lukua $0$. Koska funktion arvot lähestyvät eri lukua riippuen siitä, kummalta puolelta kohtaa $x = 1$ lähestytään, ei funktiolla $f$ ole raja-arvoa kohdassa $x = 1$.
MÄÄRITELMÄ: FUNKTION RAJA-ARVO
Oletetaan, että funktio $f$ on määritelty kohdan $a$ läheisyydessä sen molemmilla puolilla. Funktiolla $f$ on kohdassa $a$ raja-arvo $b$, jos muuttujan arvojen lähestyessä lukua $a$ kummalta puolelta tahansa, funktion $f$ arvot lähestyvät lukua $b$. Lähestymisen pitää olla sellaista, että tulemalla tarpeeksi lähelle kohtaa $a$ funktion $f$ arvot saadaan niin lähelle lukua $b$ kuin vain halutaan.
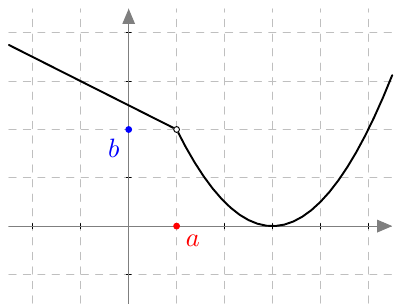
Jos funktiolla $f$ on kohdassa $a$ raja-arvo $b$, niin merkitään $$\lim_{x \rightarrow a} f(x) = b.$$ Voidaan myös käyttää merkintää $$f(x) \rightarrow b, \ \text{ kun } \ x \rightarrow a.$$
Raja-arvon kannalta ei ole mitään merkitystä sillä, onko funktio määritelty tarkasteltavassa kohdassa vai ei. Oleellista on vain se, lähestyvätkö funktion arvot jotain tiettyä arvoa, kun tarkastelukohtaa lähestytään kummasta suunnasta tahansa.
Funktion raja-arvo
Tutki alla olevaa kuvaa.
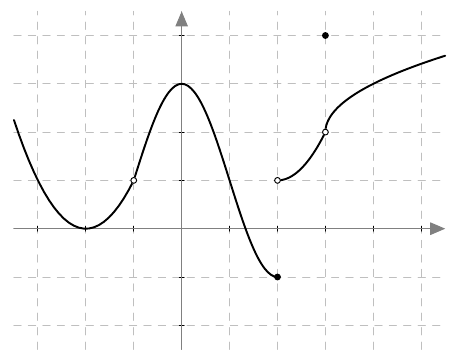
- Onko funktiolla $f$ raja-arvo kohdassa
- $x = -1$
- $x = 0$
- $x = 2$
- $x = 3$?
- Jos a-kohdassa raja-arvo on olemassa, mikä se on? Käytä vastausten ilmoittamiseen merkintätapaa $$\lim_{x \rightarrow a} f(x) = b.$$
- Onko välillä $[-3, 5]$ jokin kohta, jossa funktio $f$ ei ole määritelty?
VASTAUS
- Funktiolla $f$ on raja-arvo kohdissa $x = -1$, $x = 0$ ja $x = 3$. Funktiolla $f$ ei ole raja-arvoa kohdassa $x = 2$.
- Raja-arvot ovat seuraavat: \begin{align*} \lim_{x \rightarrow -1} f(x) &= 1 \\[1mm] \lim_{x \rightarrow 0} f(x) &= 3 \\[1mm] \lim_{x \rightarrow 3} f(x) &= 2 \end{align*}
- Funktio $f$ ei ole määritelty kohdassa $x = -1$.
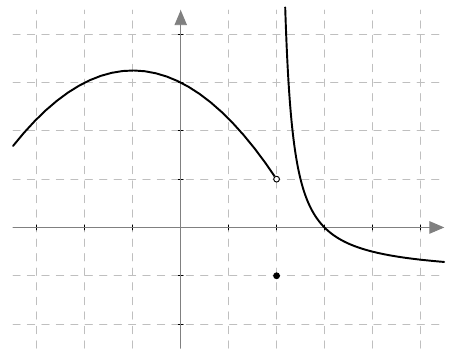
Joskus funktion raja-arvoa ei ole olemassa tarkastelukohdassa, koska funktion arvot kasvavat tai pienenevät rajatta tämän kohdan läheisyydessä. Esimerkiksi alla on näkyvissä osa funktion $g$ kuvaajasta. Siitä nähdään, että funktio $g$ on kyllä määritelty välin $[-3,5]$ jokaisessa pisteessä, mutta funktiolla $f$ ei ole raja-arvoa kohdassa $x = 2$. Tämä johtuu siitä, että funktion arvot kasvavat rajatta, kun kohtaa $x = 2$ lähestytään oikealta.
Funktion raja-arvo
Tutki alla olevaa kuvaa.
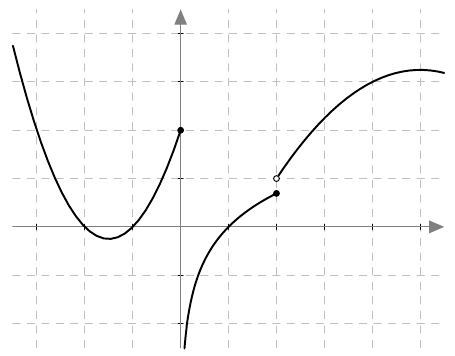
- Onko funktiolla $f$ raja-arvo kohdassa
- $x = -3$
- $x = 0$
- $x = 1$
- $x = 2$
- $x = 4$?
- Jos a-kohdassa raja-arvo on olemassa, mikä se on? Käytä vastausten ilmoittamiseen merkintätapaa $$\lim_{x \rightarrow a} f(x) = b.$$
- Onko välillä $[-3, 5]$ jokin kohta, jossa funktio $f$ ei ole määritelty?
VASTAUS
- Funktiolla $f$ on raja-arvo kohdissa $x = -3$, $x = 1$ ja $x = 4$. Funktiolla $f$ ei ole raja-arvoa kohdissa $x = 0$ ja $x = 2$.
- Raja-arvot ovat seuraavat: \begin{align*} \lim_{x \rightarrow -3} f(x) &= 2 \\[1mm] \lim_{x \rightarrow 1} f(x) &= 0 \\[1mm] \lim_{x \rightarrow 4} f(x) &= 3 \end{align*}
- Funktio $f$ on määritelty koko välillä $[-3, 5]$. Kun kohtaa $x = 0$ lähestytään oikealta, funktion arvot pienenevät rajatta.
Funktion raja-arvo
Määritellään funktio $f$ seuraavasti: $$f(x) = \begin{cases} 0{,}5x^2 + x - 4, &\text{ jos $\ x \leq 2$} \\ -x^2 + 8x - 11, &\text{ jos $\ x > 2$}. \end{cases} $$
- Piirrä funktion $f$ kuvaaja välillä $[-3, 5]$ teknisellä apuvälineellä. Ohjevideo Texas Nspirellä piirtämiseen löytyy täältä.
- Määritä kuvan avulla funktion $f$ raja-arvo kohdassa $x = 2$ tai selitä, miksi sitä ei ole olemassa.
VASTAUS
- Raja-arvoa ei ole olemassa kohdassa $x = 2$, sillä funktion arvot lähestyvät eri lukuja riippuen siitä, lähestytäänkö kohtaa $x = 2$ vasemmalta vai oikealta.
Monissa tilanteissa funktion raja-arvo tarkastelukohdassa voidaan määrittää funktion lausekkeen avulla. Esimerkiksi voidaan tutkia, onko funktiolla $f(x) = x^2-9$ raja-arvoa kohdassa $x = 5$. Päätellään, että jos $x \rightarrow 5$, niin $$x^2 - 9 \rightarrow 5^2 - 9 = 25 - 9 = 16.$$ Tulos ei riipu siitä, mistä suunnasta kohtaa $x = 5$ lähestytään. Funktiolla $f$ on siis kohdassa $x = 5$ raja-arvo $$\lim_{x \rightarrow 5} f(x) = 16.$$
Funktion raja-arvo
Määritä $\ {\displaystyle \lim_{x \rightarrow 4} f(x)}\ $ tai selitä, miksi raja-arvoa ei ole olemassa, jos
- $f(x) = \frac{7}{8}x-3$
- $f(x) = x^2 + 2x - 4$
- $f(x) = \sqrt{x} - x$
- $f(x) = 9$.
VASTAUS
- ${\displaystyle \lim_{x \rightarrow 4} f(x)} = \frac{1}{2}$
- ${\displaystyle \lim_{x \rightarrow 4} f(x)} = 20$
- ${\displaystyle \lim_{x \rightarrow 4} f(x)} = -2$
- ${\displaystyle \lim_{x \rightarrow 4} f(x)} = 9$
Paloittain määriteltyjen funktioiden raja-arvoja voidaan tutkia samaan tapaan lausekkeiden avulla. Tällöin täytyy huomata, että funktio saattaa olla määritelty eri tavoin tarkastelukohdan eri puolilla. Tarkastelukohtaa pitää sen vuoksi lähestyä erikseen sekä oikealta että vasemmalta. Lähestymissuunta ilmaistaan raja-arvon merkinnässä merkeillä $+$ ja $-$.
Vasemmalta lähestyminen: $x \rightarrow c-$

Oikealta lähestyminen: $x \rightarrow c+$

Jos esimerkiksi tutkitaan, onko funktiolla $$f(x) = \begin{cases} \dfrac{x^2+2x+4}{4}, &\text{ jos $\ x < -2$} \\[2mm] 2-\sqrt{x + 3}, &\text{ jos $\ x \geq -2$} \end{cases} $$ raja-arvoa kohdassa $x = -2$, verrataan vasemman- ja oikeanpuoleista raja-arvoa toisiinsa: \begin{align*} \lim_{x \rightarrow (-2)-} f(x) &= \lim_{x \rightarrow (-2)-}\dfrac{x^2+2x+4}{4} \\[2mm] &= \frac{(-2)^2 + 2\cdot(-2) + 4}{4} \\[2mm] &= \frac{4-4+4}{4} = 1 \end{align*} ja \begin{align*} \lim_{x \rightarrow (-2)+} f(x) &= \lim_{x \rightarrow (-2)+} (2-\sqrt{x + 3}) \\[1mm] &= 2 - \sqrt{-2+3} \\[1mm] &= 2- \sqrt{1} = 1 \end{align*} Tulos ei riipu lähestymissuunnasta, joten funktiolla $f$ on kohdassa $x = -2$ raja-arvo $$ \lim_{x \rightarrow -2} f(x) = 1. $$
Funktion raja-arvo
Määritä $\ {\displaystyle \lim_{x \rightarrow 10} f(x)}\ $ tai selitä, miksi raja-arvoa ei ole olemassa, jos $$f(x) = \begin{cases} 9x -x^2 + 3, &\text{ jos $\ x \leq 10$} \\[1mm] \sqrt{x^2 + 21} - 4, &\text{ jos $\ x > 10$}. \end{cases} $$
VASTAUS
Raja-arvoa ei ole olemassa, sillä $$ \lim_{x \rightarrow 10-} f(x) = -7 $$ mutta $$ \lim_{x \rightarrow 10+} f(x) = 7. $$
Funktion jatkuvuus
Edellisessä kappaleessa havaittiin, että funktiolla voi jossakin kohdassa olla raja-arvo, joka poikkeaa funktion arvosta. Esimerkiksi alla olevasta kuvasta nähdään, että $$\lim_{x \rightarrow -1} f(x) = -2$$ ja $$f(-1) = 1.$$ 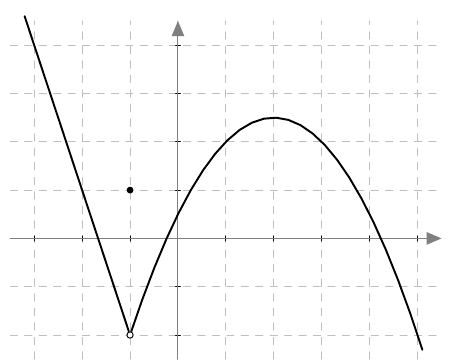
Tällaisessa tilanteessa sanotaan, että funktio $f$ ei ole jatkuva kohdassa $x = -1$.
MÄÄRITELMÄ: FUNKTION JATKUVUUS
Oletetaan, että funktio $f$ on määritelty kohdassa $a$. Funktio $f$ on jatkuva kohdassa $a$, jos $$\lim_{x \rightarrow a} f(x) = f(a).$$
Määritelmän mukaan funktio $f$ on siis jatkuva kohdassa $a$, jos sillä on kohdassa $a$ raja-arvo, joka on sama kuin funktion arvo kohdassa $a$.
Jos funktiolla ei ole raja-arvoa kohdassa $a$, funktio ei ole siinä jatkuva. Tämä voi näkyä funktion kuvaajassa hyppäyksenä, kuten esimerkiksi alla kohdassa $x = 2$.
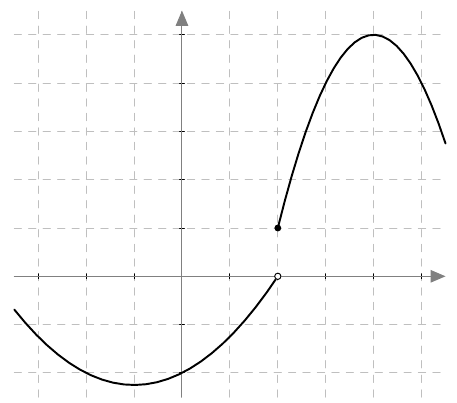
Funktion kuvaajassa näkyy hyppäyksenä myös tilanne, jossa raja-arvo on kyllä olemassa mutta poikkeaa funktion arvosta, kuten esimerkiksi alla kohdassa $x = -1$.

Yllä näkyvä funktio ei siis ole jatkuva kohdassa $x = -1$.
Funktion jatkuvuus
Tutki alla olevaa kuvaa.

Onko funktio $f$ jatkuva kohdassa
- $x = -3$
- $x = 0$
- $x = 1$
- $x = 2$
- $x = 4$?
VASTAUS
- On jatkuva.
- Ei ole jatkuva.
- On jatkuva.
- Ei ole jatkuva.
- On jatkuva.
Funktion jatkuvuus
Tutkitaan funktiota $g(x) = -x^2 + 2x + 2$.
- Määritä $\ {\displaystyle \lim_{x \rightarrow 3} g(x)}\ $ tai selitä, miksi raja-arvoa ei ole olemassa.
- Määritä $g(3)$.
- Onko funktio $g$ jatkuva kohdassa $x = 3$? Selitä omin sanoin.
- Piirrä funktion $g$ kuvaaja välillä $[-1,4]$ ja tarkista, ettei se ole ristiriidassa vastaustesi kanssa.
VASTAUS
- ${\displaystyle \lim_{x \rightarrow 3} g(x)} = -1$.
- $g(3) = -1$
- Funktio $g$ on jatkuva kohdassa $x = 3$, sillä funktion $g$ raja-arvo on tässä kohdassa sama kuin funktion $g$ arvo.
Edellä on tarkasteltu funktion jatkuvuutta aina jossain yksittäisessä kohdassa. Seuraavaksi siirrytään tarkastelemaan tilanteita, joissa funktio on jatkuva jollakin lukusuoran välillä tai jopa koko lukusuoralla. Tällaisia funktioita ovat esimerkiksi polynomifunktiot, joihin perehdyttiin kurssissa MAA2.
Alla olevassa määritelmässä tarkastellaan sekä avoimia että suljettuja välejä. Avoimen välin mitä tahansa pistettä voidaan lähestyä sekä vasemmalta että oikealta, mutta suljetun välin päätepisteitä voidaan lähestyä vain yhdestä suunnasta: vasenta päätepistettä oikealta ja oikeaa päätepistettä vasemmalta.
MÄÄRITELMÄ: FUNKTION JATKUVUUS VÄLILLÄ
Funktio $f$ on jatkuva avoimella välillä $\pa a, b\pe$, jos se on jatkuva jokaisessa välin $\pa a, b\pe$ pisteessä.
Funktio $f$ on jatkuva suljetulla välillä $[a,b]$, jos seuraavat ehdot toteutuvat:
- funktio $f$ on jatkuva avoimella välillä $\pa a, b\pe$
- ${\displaystyle \lim_{x \rightarrow a+} f(x)} = f(a)$
- ${\displaystyle \lim_{x \rightarrow b-} f(x)} = f(b)$.
Määritelmää voidaan havainnollistaa alla näkyvän funktion $f$ kuvaajan avulla. Kuvaajasta havaitaan, että funktio on jatkuva kaikissa muissa kohdissa paitsi kohdassa $x = 1$. Jos kohtaa $x = 1$ lähestytään oikealta, funktion arvot kasvavat rajatta, mutta jos kohtaa $x = 1$ lähestytään vasemmalta, funktion arvot lähestyvät lukua $-2$. Funktiolla ei tämän vuoksi ole raja-arvoa kohdassa $x = 1$ eikä se siten ole siinä jatkuva.
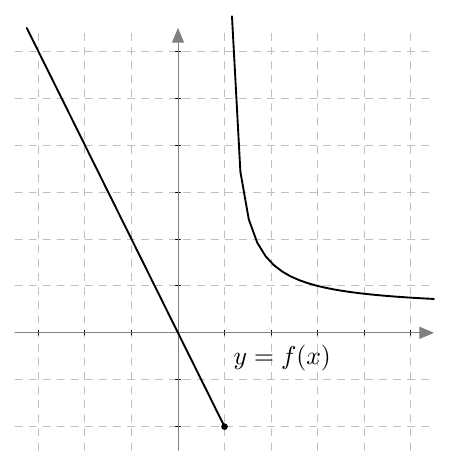
Tarkastellaan sitten funktion jatkuvuutta suljetuilla väleillä $[-2,1]$ ja $[1,3]$.
- suljetulla välillä $[-2,1]$ funktio $f$ on jatkuva, sillä se on jatkuva avoimella välillä $\pa -2, 1 \pe$ ja lisäksi \begin{align*} \lim_{x \rightarrow -2+} f(x) &= 4 = f(-2) \\ \lim_{x \rightarrow 1-} f(x) &= -2 = f(1) \end{align*}
- suljetulla välillä $[1,3]$ funktio $f$ ei ole jatkuva, sillä $f(1) = -2$ mutta funktion arvot kasvavat rajatta, kun kohtaa $x = 1$ lähestytään oikealta.
Funktion jatkuvuus
Tarkastele alla näkyvää funktion $g$ kuvaajaa.
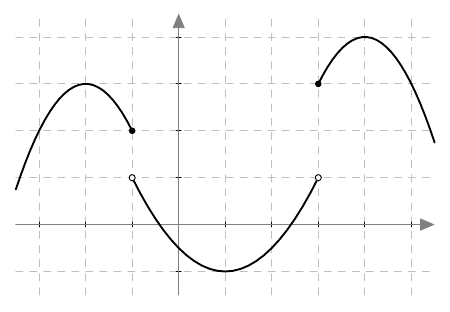 Onko funktio $g$ jatkuva välillä
Onko funktio $g$ jatkuva välillä
- $\pa -1, 3 \pe$
- $[-1,3]$
- $[3,5]$
- $\pa -3, 3 \pe$?
Perustele vastauksesi omin sanoin.
VASTAUS
- Kyllä.
- Ei.
- Kyllä.
- Ei.
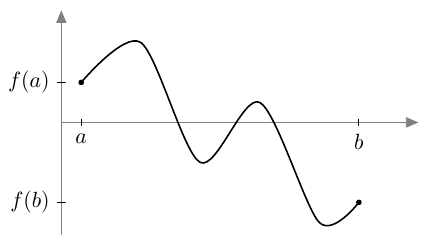
On mahdollista osoittaa, että jos suljetulla välillä jatkuva funktio saa välin päätepisteissä erimerkkiset arvot, on funktiolla tällä välillä ainakin yksi nollakohta. Tämä tulos tunnetaan nimellä Bolzanon lause. Sen todisti ensimmäisenä tsekkiläinen matemaatikko Bernard Bolzano vuonna 1817. Kuvasta katsottuna Bolzanon lause on helppo uskoa todeksi, mutta yleispätevän perustelun esittäminen on sen verran työlästä, että sitä käsitellään vasta yliopistotasolla.
TEOREEMA
Jos funktio $f$ on määritelty ja jatkuva suljetulla välillä $[a,b]$ ja jos funktion arvot $f(a)$ ja $f(b)$ ovat erimerkkiset, niin funktiolla on (ainakin yksi) nollakohta avoimella välillä $\pa a, b\pe$.

Huomaa, että jos Bolzanon lauseen ehdot täyttyvät, voi funktiolla olla useampikin nollakohta tarkasteluvälillä. Tällainen tilanne on alla olevassa kuvassa.
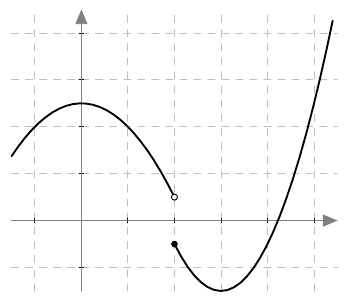
Nollakohdan olemassaolon kannalta on oleellista, että funktio on jatkuva suljetulla välillä $[a,b]$. Esimerkiksi seuraavan kuvan tilanteessa funktio $f$ on kyllä määritelty suljetulla välillä $[-1,2]$ ja saa sen päätepisteissä erimerkkiset arvot: $f(-1) = 2$ ja $f(2) = -0{,}5$. Lisäksi funktio on jatkuva avoimella välillä $\pa -1, 2 \pe$, mutta sillä ei ole nollakohtaa välillä $\pa -1,2 \pe$.
Bolzanon lausetta voidaan hyödyntää esimerkiksi polynomifunktioiden nollakohtien etsimisessä ja polynomiyhtälöiden ratkaisussa, sillä polynomifunktiot ovat jatkuvia millä tahansa lukusuoran välillä. Tämän teoreeman täsmällinen todistus on niin työläs, että siihen tutustutaan vasta yliopistotasolla.
TEOREEMA
Polynomifunktio on kaikkialla jatkuva.
Bolzanon lauseen ja teoreeman 2 käyttöä harjoitellaan seuraavassa tehtävässä.
Jatkuvan funktion nollakohdat
Tutkitaan funktiota $f(x) = x^3 -4x + 2$.
- Perustele huolellisesti, että funktiolla $f$ on ainakin yksi nollakohta välillä $\pa -3, 2\pe$. (Älä kuitenkaan piirrä funktion kuvaajaa vielä.)
- Laske funktion $f$ arvo kohdassa $x = -2$. Mitä voit nyt päätellä funktion $f$ nollakohtien lukumäärästä ja sijainnista?
- Laske funktion $f$ arvo kohdassa $x = 1$. Mitä voit nyt päätellä funktion $f$ nollakohtien lukumäärästä ja sijainnista?
- Tarkista vastauksesi piirtämällä funktion $f$ kuvaaja.
VASTAUS
- Funktio $f$ on polynomifunktio ja sen vuoksi jatkuva välillä $[-3,2]$. Lisäksi $f(-3) = -13 < 0$ ja $f(2) = 2 >0$, joten Bolzanon lauseen mukaan sillä on ainakin yksi nollakohta välillä $\pa -3, 2\pe$.
- Koska $f(-3) = -13 < 0$ ja $f(-2) = 2 > 0$, niin funktiolla $f$ on ainakin yksi nollakohta välillä $\pa -3, -2\pe$.
- Koska $f(-3) = -13 < 0$, $f(-2) = 2 > 0$, $f(1) = -1 < 0$ ja $f(2) = 2 >0$, niin funktiolla $f$ on ainakin yksi nollakohta väleillä $\pa -3, -2\pe$, $\pa -2, 1\pe$ ja $\pa 1, 2\pe$. Funktiolla $f$ on siis ainakin kolme nollakohtaa.
Jos funktio saa kahdessa eri kohdassa samanmerkkiset arvot, niiden välillä saattaa olla olemassa nollakohtia tai sitten ei. Tätä tutkitaan seuraavassa tehtävässä.
Jatkuvan funktion nollakohdat
Keksi esimerkki polynomifunktiosta, joka saa positiivisen arvon kohdissa $x = -2$ ja $x = 2$ ja jolla
- ei ole nollakohtaa välillä $\pa -2, 2 \pe$
- on nollakohta välillä $\pa -2, 2 \pe$
Tarkista vastauksesi piirtämällä keksimäsi funktioiden kuvaajat.
VINKKI
Kokeile esimerkiksi erilaisia toisen asteen polynomifunktioita.
Seuraavissa tehtävissä harjoitellaan Bolzanon lauseen soveltamista polynomiyhtälöiden ratkaisujen tutkimiseen.
Jatkuvan funktion nollakohdat
Tehtävänä on osoittaa, että yhtälöllä $x^4 - 5x^3 + 6 = 0$ on ratkaisu, jonka kaksidesimaalinen likiarvo on $4{,}95$.
- Mikä on pienin kolmidesimaalinen luku, joka pyöristyy luvuksi $4{,}95$?
- Mikä on suurin kolmidesimaalinen luku, joka pyöristyy luvuksi $4{,}95$?
- Tehtävän voi ratkaista Bolzanon lauseen avulla, mutta mihin funktioon ja mihin suljettuun väliin sitä pitää soveltaa?
- Perustele, että yhtälöllä $x^4 - 5x^3 + 6 = 0$ on ratkaisu, jonka kaksidesimaalinen likiarvo on $4{,}95$.
VASTAUS
- Pienin sopiva luku on $4{,}945$.
- Suurin sopiva luku on $4{,}954$.
- Funktioon $f(x) = x^4 - 5x^3 + 6$ ja väliin $[4{,}945; \,4{,}954]$.
- Funktio $f$ on polynomifunktio, joten se on jatkuva välillä $[4{,}945; \,4{,}954]$. Lisäksi $f(4{,}945) \approx -0{,}65 < 0$ ja $f(4{,}954) \approx 0{,}41 > 0$, joten funktiolla $f$ on ainakin yksi nollakohta välillä $\pa 4{,}945; \,4{,}954\pe$ .
Jatkuvan funktion nollakohdat
Jatketaan yhtälön $x^4 - 5x^3 + 6 = 0$ tarkastelua.
- Osoita, että yhtälöllä on ainakin yksi ratkaisu välillä $\pa 1{,}0;\,1{,}5 \pe.$
- Pienennä tarkasteluväliä askel askeleelta niin, että saat tarkempaa tietoa ratkaisun likiarvosta. Tavoitteena on määrittää ratkaisun likiarvo yhden desimaalin tarkkuudella, joten tarkasteluväli pitää saada niin pieneksi, että sen molempien päätepisteiden yksidesimaaliset likiarvot ovat samat.
- Mikä on etsityn ratkaisun likiarvo yhden desimaalin tarkkuudella?
VASTAUS
- Tarkasteluväliksi sopii esimerkiksi $[1{,}15;\, 1{,}24]$ tai $[1{,}15;\, 1{,}20]$
- Likiarvo on $1{,}2$.
Jatkuvuus ja derivoituvuus
Ensimmäisessä luvussa opittiin, että funktion derivaatta on funktion kuvaajalle piirretyn tangentin kulmakerroin. Esimerkiksi alla näkyvän funktion $f$ derivaatta kohdassa $x = 2$ on $$f'(2) = -0{,}5.$$ 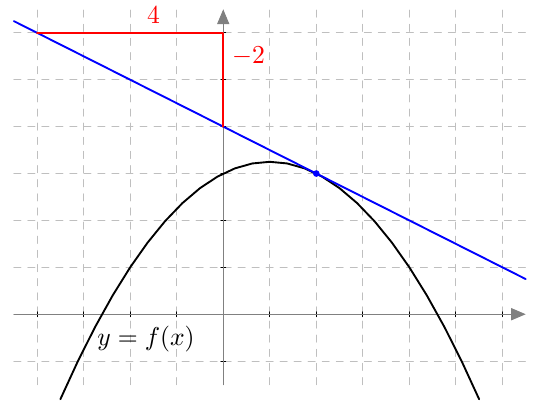
Funktion kuvaajalle ei kuitenkaan aina ole mahdollista piirtää yksikäsitteistä tangenttia. Erityisesti kohdat, joissa funktio ei ole jatkuva, tuottavat hankaluuksia. Miten esimerkiksi pitäisi piirtää tangentti alla näkyvän funktion kuvaajan kohtaan $x = 3$?
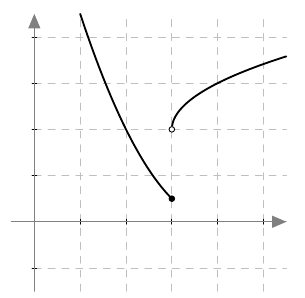
Alla näkyy kaksi suoraa, jotka sivuavat funktion kuvaajaa kohdassa $x = 3$. Yksikäsitteistä tangettia on mahdotonta piirtää, joten funktiolla $f$ ei ole derivaattaa kohdassa $x = 3$. Tämä voidaan ilmaista myös sanomalla, että funktio $f$ ei ole derivoituva kohdassa $x = 3$.
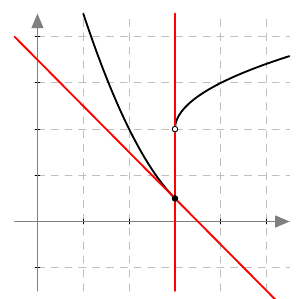
On mahdollista osoittaa yleispätevästi, että funktio voi olla derivoituva vain siinä tapauksessa, että se on jatkuva:
TEOREEMA
Jos funktiolla on derivaatta kohdassa $a$, niin funktio on jatkuva kohdassa $a$.
Teoreemasta 3 seuraa, että jos funktio ei ole jatkuva, se ei missään tapauksessa voi olla derivoituva. Toisaalta vaikka funktio olisi jatkuva, se ei välttämättä ole derivoituva. Esimerkiksi alla on näkyvissä itseisarvofunktion $$f(x) = \left|x\right|$$ kuvaaja. Se on katkeamaton käyrä, mistä voidaan päätellä, että itseisarvofunktio on jatkuva.
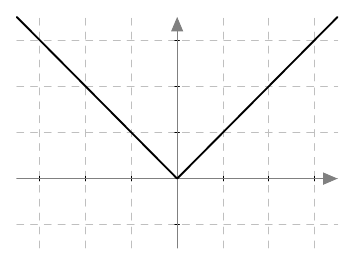
Havaitaan, että kohtaan $x = 0$ on mahdotonta piirtää yksikäsitteistä tangenttia:
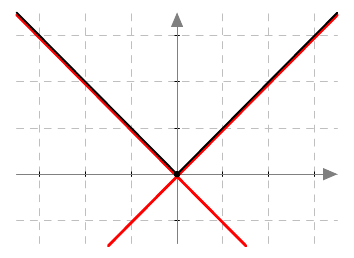
Itseisarvofunktio $f(x) = \left|x\right|$ ei siten ole derivoituva kohdassa $x = 0$, vaikka onkin siinä jatkuva.
Jatkuvuus ja derivoituvuus
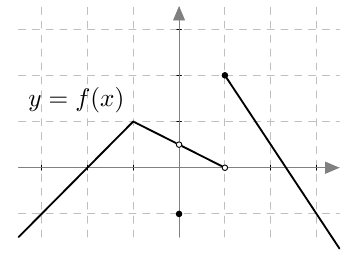
Alla on näkyvissä oleelliset osat funktion $f$ kuvaajasta. Päättele kuvaajan perusteella,
- missä kohdissa funktio $f$ ei ole jatkuva
- missä kohdissa funktio $f$ ei ole derivoituva
- mikä on funktion derivaatan arvo niissä kohdissa, joissa se on olemassa.
VASTAUS
- Kohdissa $x = 0$ ja $x = 1$.
- Kohdissa $x = -1$, $x = 0$ ja $x = 1$.
-
- Jos $x < -1$, niin $f'(x) = 1$.
- Jos $-1 < x < 0$ tai $0 < x < 1$, niin $f'(x) = -0{,}5$.
- Jos $x > 1$, niin $f'(x) = -1{,}5$.
TEHTÄVÄSARJA II
Funktion raja-arvo
Määritellään funktio $f$ seuraavasti: $$f(x) = \begin{cases} -3x-5, &\text{ jos $\ x < -1$} \\ 1, &\text{ jos $\ x = -1$}\\ -x^2 + 4x + 3, &\text{ jos $\ x > -1$}. \end{cases} $$
- Piirrä funktion $f$ kuvaaja välillä $[-3, 5]$. Jos käsin piirtäminen tuottaa haasteita, niin voit piirtää kuvaajan osat teknisellä apuvälineellä ja kopioida ne paperille funktion määritelmän mukaisilla väleillä. Esimerkiksi suorasta $y=-3x-5$ otetaan mukaan vain se osa, jossa $x<-1$.
- Määritä kuvan avulla funktion $f$ raja-arvo kohdassa $x = -1$ tai selitä, miksi sitä ei ole olemassa.
VASTAUS
- Raja-arvo on olemassa: \begin{align*} \lim_{x \rightarrow -1} f(x) &= -2 \end{align*}
Funktion raja-arvo
Määritä $\ {\displaystyle \lim_{x \rightarrow 5} f(x)}\ $ tai selitä, miksi raja-arvoa ei ole olemassa, jos $$f(x) = \begin{cases} \dfrac{30}{x} - x + 1, &\text{ jos $\ x \leq 5$} \\[2mm] \sqrt{4x -4} - 2, &\text{ jos $\ x > 5$}. \end{cases} $$
VASTAUS
Tulos ei riipu siitä, kummasta suunnasta kohtaa $x = 5$ lähestytään, joten ${\displaystyle \lim_{x \rightarrow 5} f(x)} = 2$.
Funktion jatkuvuus
Määritellään funktio $f$ seuraavasti: $$f(x) = \begin{cases} 0{,}5x^2 + x - 5, &\text{ jos $\ x \leq 2$} \\ 8x +1 + a, &\text{ jos $\ x > 2$}. \end{cases} $$
- Laske, mitä on $f(2)$.
- Päättele, mitä funktion arvot lähestyvät, jos lähestytään kohtaa $x = 2$ oikealta.
- Määritä vakiolle $a$ sellainen arvo, että funktio $f$ on jatkuva kohdassa $x = 2$.
VASTAUS
- $f(2) = -1$.
- $17 + a$
- $a = -18$.
Funktion jatkuvuus
Määritä vakiolle $a$ sellainen arvo, että funktio $$f(x) = \begin{cases} x-1, &\text{ jos $\ x \leq a$} \\ x^2 -3, &\text{ jos $\ x > a$} \end{cases} $$ on jatkuva kaikkialla.
VASTAUS
$a = -1$ tai $a = 2$
Jatkuvuus ja derivoituvuus
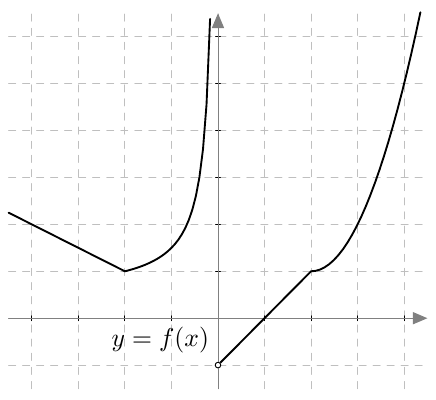
Päättele alla olevan kuvaajan avulla,
- onko välillä $[4,-4]$ jokin kohta, jossa funktio $f$ ei ole määritelty
- onko funktion $f$ määrittelyjoukossa jokin kohta, jossa funktio ei ole jatkuva
- onko funktion $f$ määrittelyjoukossa jokin kohta, jossa funktio ei ole derivoituva.
VASTAUS
- Funktio $f$ ei ole määritelty kohdassa $x = 0$.
- Määrittelyjoukossaan funktio $f$ on jatkuva.
- Funktion $f$ määrittelyjoukossa on kaksi kohtaa, joissa funktio ei ole derivoituva: kohdat $x = -2$ ja $x = 2$.
Funktion jatkuvuus
Oletetaan, että funktio $f$ on määritelty ja jatkuva suljetulla välillä $[a,b]$. Tehtävänä on osoittaa, että funktio saa välillä $\pa a, b\pe$ ainakin kerran jokaisen arvon, joka on päätepistearvojen $f(a)$ ja $f(b)$ välissä.
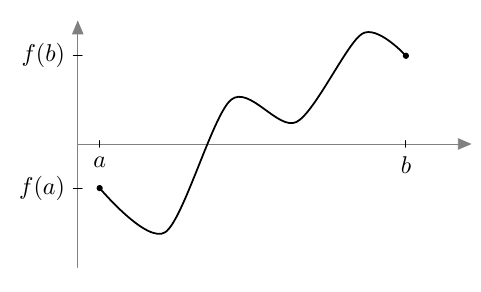
Ohje: Oleta, että $f(a) < c < f(b)$ ja sovella Bolzanon lausetta funktioon $g(x) = f(x) - c$. Muista tarkistaa, että funktio $g$ toteuttaa Bolzanon lauseen ehdot, ks. teoreema 1.
VASTAUS
Funktio $g$ on määritelty välillä $[a,b]$. Koska funktio $f$ on jatkuva ja funktio $g$ saadaan siitä vähentämällä vakio $c$, on myös funktio $g$ jatkuva (niiden kuvaajat ovat muuten identtiset mutta koordinaatistossa eri korkeudella). Lisäksi $g(a) = f(a)-c < 0$ ja $g(b) = f(b) - c > 0$, joten Bolzanon lauseen nojalla funktiolla $g$ on ainakin yksi nollakohta välillä $\pa a, b\pe$. Tästä seuraa, että funktiolla $f$ on välillä $\pa a, b\pe$ ainakin yksi kohta, jossa se saa arvon $c$. Tämä päättely toimii mille tahansa vakiolle $c$, jolle pätee $f(a) < c < f(b)$, joten funktio saa välillä $\pa a, b\pe$ ainakin kerran jokaisen arvon, joka on päätepistearvojen $f(a)$ ja $f(b)$ välissä.
TEHTÄVÄSARJA III
Pisteen $(2,3)$ kautta kulkeva suora leikkaa positiivisen $x$-akselin pisteessä $A = (t,0)$ ja positiivisen $y$-akselin pisteessä $B$. Merkitään $C = (2,0)$ ja tarkastellaan kolmiota $ABC$.
- Piirrä tilanteesta kuva.
- Muodosta funktio $f(t)$, joka ilmaisee kolmion ABC pinta-alan.
- Määritä pinta-alan raja-arvo, kun piste $A$ lähestyy pistettä $C$.
VASTAUS
- $f(t) = \dfrac{3t}{2}$
- Kun piste $A$ lähestyy pistettä $C$, niin $t \rightarrow 2$. Raja-arvo on $$ \lim_{t \rightarrow 2} f(t) = \lim_{t \rightarrow 2}\dfrac{3t}{2} = 3. $$
Polynomifunktio $f$ toteuttaa välillä $[0,2]$ ehdon $$ 0 < f(x) < 4. $$ Tehtävänä on osoittaa, että kyseisellä välillä on ainakin yksi kohta $a$, jossa $$f(a) = a^2.$$
- Onko funktio $f$ jatkuva välillä $[0,2]$?
Vinkki: teoreema 2. - Merkitään $g(x) = f(x) - x^2$. Onko funktio $g$ jatkuva välillä $[0,2]$?
- Mitä voit päätellä funktiosta $g$ Bolzanon lauseen avulla? Kertaa tarvittaessa teoreema 1 ja tutki, täyttääkö funktio sen ehdot.
- Miten perustelet alkuperäisen väitteen, että funktiolla $f$ on välillä $[0,2]$ ainakin yksi kohta $a$, jossa $f(a) = a^2$?
VASTAUS
- Funktio $f$ on polynomifunktio, joten se on jatkuva kaikkialla.
- Myös $g$ on polynomifunktio, joten sekin on jatkuva kaikkialla.
- Bolzanon lauseen ehdot täyttyvät, joten funktiolla $g$ on ainakin yksi nollakohta välillä $\pa 0, 2 \pe$.
- Jos $g(x) = 0$, niin $f(x) = x^2$. Etsityksi kohdaksi $a$ kelpaa siis funktion $g$ nollakohta.
Oletetaan, että funktio $f \colon [0,5] \to \R$ on derivoituva, $f\left(\frac{1}{2}\right) = 1$ ja derivaatalle pätee $$ \frac{1}{4} \leq f'(x) \leq \frac{3}{4}. $$ Mitä voidaan päätellä funktion arvosta $f(3)$?
[Pitkä S2009/13]
Vinkki: Muista, että derivaatta kertoo funktion arvojen muutosnopeuden. Kuinka suuri $f(3)$ voi enintään olla? Miten suuri sen on vähintään oltava?
Vastaus
$\frac{13}{8} \leq f(3) \leq \frac{23}{8}$.
Funktion $f \color \R \to \R$ jakso on 2, toisin sanottuna $f(x+2) = f(x)$ kaikilla reaaliluvuilla $x$. Lisäksi on $$ f(x) = \begin{cases} 1+x, &\text{ kun $-1 \leq x \leq 0$}\\ 1-x, &\text{ kun $0 \leq x \leq 1$.} \end{cases} $$ Piirrä funktion $f$ kuvaaja. Missä pisteissä $f$ ei ole derivoituva?
Piirrä funktioiden $g$ ja $h$ kuvaajat, kun $g(x) = f(x+1)$ ja $h(x) = f(x) + f(x+1)$. Missä pisteissä nämä eivät ole derivoituvia?
[Pitkä S2004/9]
Vastaus
Funktion $f$ kuvaaja:
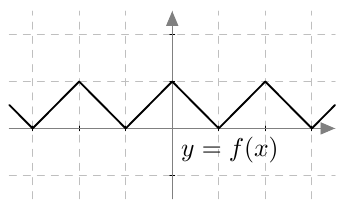
Funktio $f$ ei ole derivoituva sahalaidan kärkipisteissä eli kohdissa, joissa kuvaajan pisteiden $x$-koordinaatti on kokonaisluku.
Funktiolle $g$ pätee $g(0) = f(0+1) = f(1)$, $g(1) = f(1+1) = f(2)$ ja niin edelleen. Funktion $g$ kuvaaja:
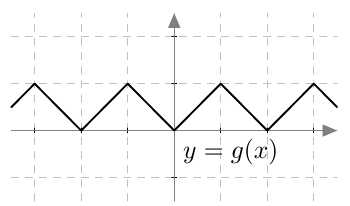
Myöskään funktio $g$ ei ole derivoituva sahalaidan kärkipisteissä eli kohdissa, joissa kuvaajan pisteiden $x$-koordinaatti on kokonaisluku.
Funktion $h$ arvo on jokaisessa kohdassa funktioiden $f$ ja $g$ arvojen summa: $h(x) = f(x) + g(x)$. Funktion $h$ kuvaaja:
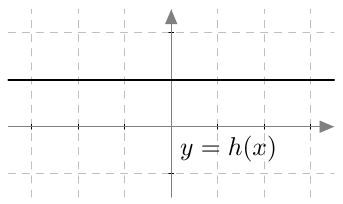
Funktio $h$ on vakiofunktio, joten se on derivoituva kaikkialla.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

