Kolmio
Luvun tavoitteet
Tämän luvun tavoitteena on, että osaat ratkaista erilaisia geometrisia ongelmia kolmioiden avulla. Osaat
- laskea kolmion pinta-alan
- tunnistaa vierus- ja ristikulmat sekä samankohtaiset kulmat ja päätellä niiden suuruuden
- perustella kolmioiden yhdenmuotoisuuden ja hyödyntää sitä geometristen ongelmien ratkaisussa
- määrittää kolmioiden sivujen pituuksia ja kulmien suuruuksia Pythagoraan lauseen, trigonometristen suhteiden sekä sini- ja kosinilauseiden avulla
- päätellä suplementtikulman sinin ja kosinin arvot.
Kolmion pinta-ala ja kulmat
Kolmioita voidaan käyttää apuna monien geometristen ongelmien ratkaisemisessa. Aloitammekin tämän kurssin palauttamalla mieleen kolmioiden geometrisia ominaisuuksia.
Kolmioiden ja muiden tasokuvioiden pinta-alan laskemiseksi tarvitaan sopimus siitä, mitä pinta-alalla tarkoitetaan. Lähtökohdaksi voidaan ottaa suorakulmion pinta-ala. Sovitaan siis ensin, mitä suorakulmion pinta-alalla tarkoitetaan. Asetetaan seuraava määritelmä:
MÄÄRITELMÄ: SUORAKULMION PINTA-ALA
Suorakulmion pinta-ala on samasta kärjestä alkavien sivujen pituuksien tulo eli alla olevan kuvion merkinnöillä $ab$.
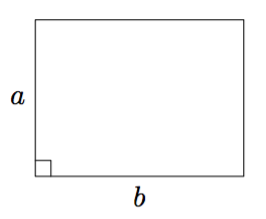
Suorakulmion pinta-ala
Kansainvälisissä aikuisten jalkapallo-otteluissa kentän leveyden on oltava vähintään 64 m ja enintään 75 m. Kentän pituuden on oltava vähintään 100 m ja enintään 110 m.
- Laske suurimman ja pienimmän mahdollisen jalkapallokentän pinta-alojen erotus.
- Kuinka monta prosenttia suurin mahdollinen kenttä on isompi kuin pienin mahdollinen kenttä?
VASTAUS
- $1\,850 \text{ m}^2$
- Noin 29 %.
Suorakulmion pinta-alan avulla saadaan johdettua lauseke kolmion pinta-alalle.
Kolmion pinta-ala
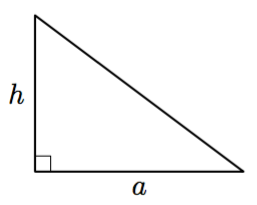
- Piirrä yllä olevan kuvan kolmio vihkoosi ja täydennä se suorakulmioksi.
- Muodosta suorakulmion pinta-alan lauseke.
- Päättele kolmion pinta-ala.
Kolmion pinta-ala
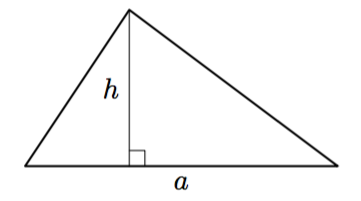
- Piirrä yllä olevan kuvan kolmio vihkoosi ja täydennä se suorakulmioksi.
Vinkki: voit esimerkiksi soveltaa edellisen tehtävän ideaa kumpaankin kuvassa näkyvään suorakulmaiseen kolmioon. - Muodosta suorakulmion pinta-alan lauseke.
- Päättele kolmion pinta-ala.
Edellisten tehtävien tulokset ovat osa seuraavaa teoreemaa. Lue teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Kolmion pinta-ala on puolet sen kannan ja korkeuden tulosta eli alla olevan kuvion merkinnöillä $$\dfrac{ah}{2}$$
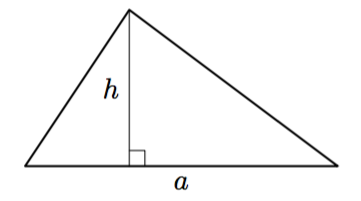
Perustelu: Kolmion korkeusjanan toinen päätepiste voi sijaita kolmion sivun päätepisteessä, kolmion sivulla tai sivun jatkeella. Tarkastellaan jokainen näistä tapauksista erikseen.
- Tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivun päätepisteessä, on käsitelty tehtävässä 1.2.

- Tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivulla, on käsitelty tehtävässä 1.3.
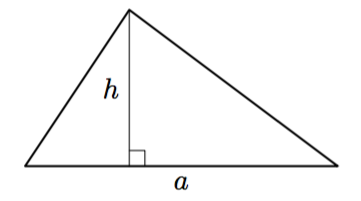
- Jos kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivun jatkeella, voidaan kolmio täydentää suorakulmaiseksi kolmioksi, jonka pinta-ala on tehtävän 1.2 nojalla $$\frac{(a+x)h}{2}.$$

Alkuperäisen kolmion pinta-ala saadaan tästä vähentämällä pienemmän suorakulmaisen kolmion pinta-ala: \begin{align*} \frac{(a+x)h}{2} - \frac{xh}{2} &= \frac{ah + xh - xh}{2} \\[1mm] &= \frac{ah}{2} \end{align*}
Kolmion pinta-ala
Harjakattoisen omakotitalon pituus on 10 m ja leveys 6 m. Ensimmäisen kerroksen korkeus on 3 m ja toisen kerroksen päätykolmioiden korkeus 2,5 m. Talo aiotaan maalata. Maalin menekiksi arvioidaan yksi litra 6,5 neliömetriä kohti. Tehtävänä on laskea, kuinka paljon maalia tarvitaan, jos talo maalataan kaksi kertaa (pohjamaalaus ja pintamaalaus). Ikkunoita ei laskelmassa oteta huomioon.

- Laske seinien kokonaispinta-ala.
- Kuinka paljon maalia kannattaa ostaa talon maalaamista varten?
VASTAUS
- Seinien kokonaispinta-ala on $111 \text{ m}^2$.
- Maalia kannattaa ostaa noin 34-35 litraa (ikkunoita ei huomioitu laskelmassa, joten tulosta ei välttämättä tarvitse pyöristää ylöspäin).
Ryhdytään seuraavaksi tutkimaan kolmion kulmia. Palautetaan aluksi mieleen joidenkin kulmien nimityksiä.
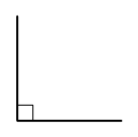
MÄÄRITELMÄ: SUORA KULMA JA OIKOKULMA
Suora kulma tarkoittaa kulmaa, jonka suuruus on $90^\circ$.
Oikokulma tarkoittaa kulmaa, jonka suuruus on $180^\circ$.
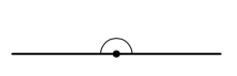
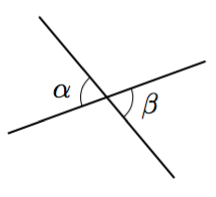
Vieruskulmat
Kulmat, joiden toinen kylki on yhteinen ja toiset kyljet muodostavat suoran, ovat vieruskulmia.
- Päättele kulman $\alpha$ suuruus alla olevassa kuvassa.
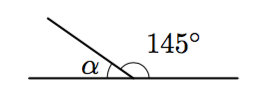
- Päättele kulman $\beta$ suuruus alla olevassa kuvassa.
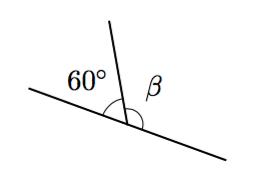
- Mitä voit päätellä vieruskulmien summasta yleisesti?
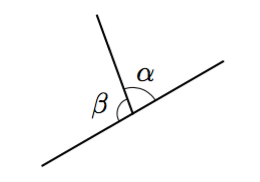
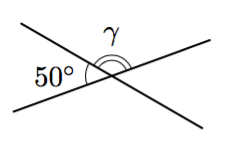
Ristikulmat
Kun kaksi suoraa leikkaa toisensa, muodostuvat vastakkaiset kulmat ovat ristikulmia.
- Päättele kulman $\gamma$ suuruus alla olevassa kuvassa.
- Päättele kulman $\beta$ suuruus alla olevassa kuvassa.
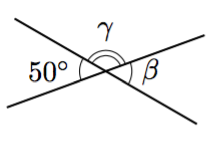
- Mitä voit päätellä ristikulmista yleisesti?
Jos suora leikkaa kahta muuta suoraa, syntyy niin sanottuja samankohtaisia kulmia. Samankohtaisuus tarkoittaa sitä, että kulmien samanniminen kylki (siis molemmilla oikea kylki tai molemmilla vasen kylki), on samalla suoralla.
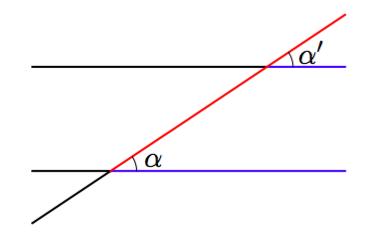
Jos kaksi muuta suoraa ovat keskenään yhdensuuntaisia, kuten yllä olevassa kuvassa, syntyvät samankohtaiset kulmat ovat yhtä suuria. Esimerkiksi yllä olevassa kuvassa kulmat $\alpha$ ja $\alpha'$ ovat samankohtaisia, sillä niiden $\textcolor{red}{\textbf{vasen}}$ kylki on samalla suoralla. Koska niiden $\textcolor{blue}{\textbf{oikeat}}$ kyljet ovat yhdensuuntaiset, ovat kulmat $\alpha$ ja $\alpha'$ yhtä suuret.
Samankohtaiset kulmat
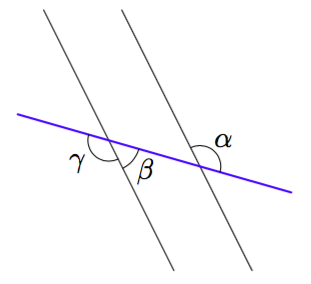
- Piirrä yllä oleva kuva vihkoosi ja merkitse siihen kulman $\alpha$ ristikulma.
- Etsi kuvasta mahdollisimman monta kulmaa, jotka ovat samankohtaisia kulman $\alpha$ kanssa.
Vinkki: etsi kulmia, joiden oikea kylki on sinisellä suoralla. - Ovatko kulmat $\alpha$ ja $\beta$ samankohtaisia? Entä kulmat $\alpha$ ja $\gamma$?
- Tiedetään, että $\alpha = 133^\circ$. Päättele kulmien $\beta$ ja $\gamma$ suuruus.
Ristikulmien ja samankohtaisten kulmien avulla voidaan näyttää, että kolmion kulmien summa on aina $180^\circ$. Tämä tehdään seuraavassa teoreemassa. Lue teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Kolmion kulmien summa on $180^\circ$.
Perustelu: Merkitään kolmion kulmia $\alpha$, $\beta$ ja $\gamma$.
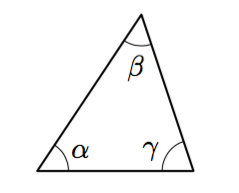
Jatketaan kolmion kahta sivua kuten alla olevassa kuvassa. Muodostuva kulma $\beta'$ on yhtä suuri kuin kulma $\beta$. Ne ovat toistensa ristikulmia.
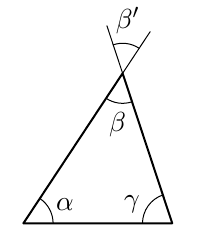
Piirretään kulman $\beta$ kärjen kautta jana, joka on yhdensuuntainen kolmion kannan kanssa samaan tapaan kuin alla olevassa kuvassa. Kulmien $\alpha'$ ja $\alpha$ vasempana kylkenä on sama suora, joten ne ovat samankohtaiset kulmat. Lisäksi niiden oikeat kyljet ovat keskenään yhdensuuntaiset, joten kulmat ovat yhtä suuret.
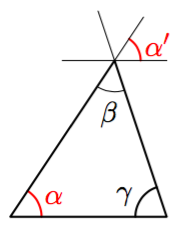
Vastaavasti kulmien $\gamma'$ ja $\gamma$ oikeana kylkenä on sama suora, joten ne ovat samankohtaiset kulmat. Lisäksi niiden vasemmat kyljet ovat keskenään yhdensuuntaiset, joten kulmat ovat yhtä suuret.
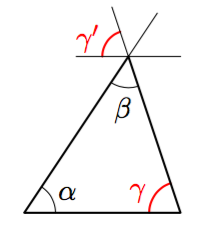
Kulmat $\alpha'$, $\beta'$ ja $\gamma'$ muodostavat yhdessä oikokulman $180^\circ$:
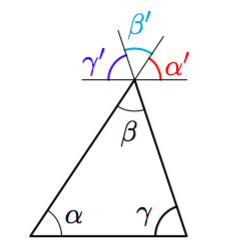
Koska $\alpha = \alpha'$, $\beta = \beta'$ ja $\gamma = \gamma'$, voidaan päätellä, että myös $$\alpha + \beta + \gamma = 180^\circ.$$
Kolmioiden yhdenmuotoisuus
Kolmioita voidaan luokitella niiden muodon mukaan. Esimerkiksi alla olevan kuvan kolmiot ovat eri kokoisia ja eri asennossa, mutta kuitenkin saman muotoisia. Tällaisia kolmioita sanotaan yhdenmuotoisiksi.
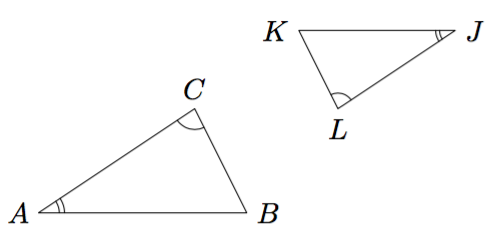
Tarkemmin kolmioiden yhdenmuotoisuus määritellään niin sanottujen vastinkulmien ja vastinsivujen avulla. Esimerkiksi yllä kulman $\sphericalangle BAC$ vastinkulma on $\sphericalangle KJL$ (nämä molemmat kulmat ovat kolmioiden lyhimpien sivujen vastaisia kulmia ja ne on merkitty kuvaan kahdella pienellä kaarella). Isomman kolmion pisimmän sivun $AB$ vastinsivu on puolestaan $JK$, joka on pienemmän kolmion pisin sivu.
Vastinkulmat ja vastinsivut
Jatka yllä olevan kuvan tarkastelua.
- Mikä on sivun $BC$ vastinsivu?
- Mikä on kulman $\sphericalangle JLK$ vastinkulma?
MÄÄRITELMÄ: KOLMIOIDEN YHDENMUOTOISUUS
Kolmiot ovat yhdenmuotoiset, jos ne toteuttavat seuraavat ehdot:
- kulma ja sen vastinkulma ovat aina yhtä suuret
- suhde $$\frac{\text{ vastinsivun pituus }}{\text{ sivun pituus }}$$ on vakio (eli sama riippumatta siitä, mitä kolmion sivua tarkastellaan).
Kolmion kulmat
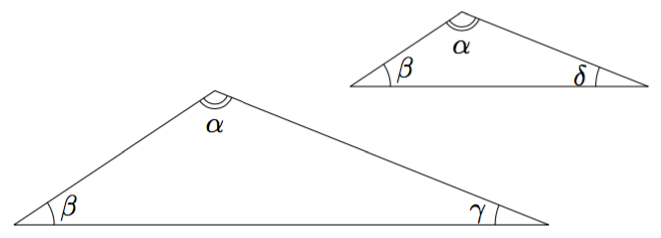
Yllä olevan kuvan vasemmanpuoleisessa kolmiossa on kaksi kulmaa, jotka ovat yhtä suuria kuin niiden vastinkulmat oikeanpuoleisessa kolmiossa. Näitä kulmia on merkitty kirjaimilla $\alpha$ ja $\beta$.
- Päättele kulman $\gamma$ suuruus teoreeman 2 avulla.
- Päättele kulman $\delta$ suuruus teoreeman 2 avulla.
- Vertaa edellisten kohtien tuloksia. Mitä voit päätellä kulmista $\gamma$ ja $\delta$?
On mahdollista osoittaa, että jos kolmion kaksi kulmaa ovat yhtä suuria kuin toisen kolmion kaksi kulmaa, niin kolmiot ovat yhdenmuotoiset:
TEOREEMA
Jos kolmiossa on kaksi kulmaa, jotka ovat yhtä suuria kuin niitä vastaavat kulmat toisessa kolmiossa, niin kolmiot ovat yhdenmuotoiset.
Perustelu: Merkitään niitä kulmia, jotka ovat molemmissa kolmioissa yhtä suuria, kirjaimilla $\alpha$ ja $\beta$ kuten alla olevassa kuvassa. Edellisessä tehtävässä pääteltiin, että tällöin myös kolmas kulma on molemmissa kolmioissa yhtä suuri.

Lisäksi pitäisi perustella, että vastinsivun pituuden suhde sivun pituuteen on aina sama eli yllä olevan kuvan mukaan $$\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'}.$$ Tämä perustelu on sen verran hankala, että se sivuutetaan. (Perustelu löytyy esimerkiksi täältä, lause 2.2.1.)
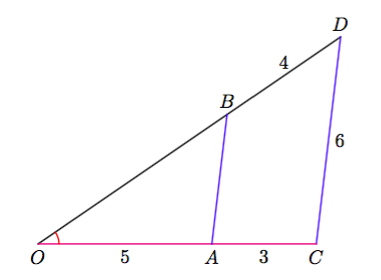
Yllä olevassa kuvassa janat $AB$ ja $CD$ ovat yhdensuuntaisia eli $AB \parallel CD$. Tämän tiedon ja KK-lauseen (teoreema 3) avulla voidaan päätellä, että kolmiot $OAB$ ja $OCD$ ovat yhdenmuotoisia:
- Kolmioilla $OAB$ ja $OCD$ on yhteinen kulma $\sphericalangle O$ (merkitty kuvaan punaisella kaarella).
- Kulmat $\sphericalangle OAB$ ja $\sphericalangle OCD$ ovat samankohtaisia, koska niiden $\textcolor{magenta}{\textbf{vasen}}$ kylki on samalla suoralla. Lisäksi niiden $\textcolor{blue}{\textbf{oikeat}}$ kyljet $AB$ ja $CD$ ovat yhdensuuntaisia, joten kulmat $\sphericalangle OAB$ ja $\sphericalangle OCD$ ovat yhtä suuria.
- Koska kolmiossa $OAB$ on kaksi kulmaa, jotka ovat yhtä suuria kuin niitä vastaavat kulmat kolmiossa $OCD$, niin kolmiot ovat yhdenmuotoiset KK-lauseen nojalla.
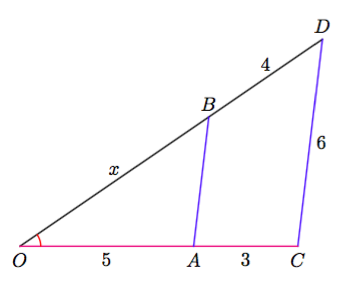
Kolmioiden yhdenmuotoisuuden avulla voidaan nyt päätellä pienemmän kolmion $OAB$ sivujen pituuksia. Esimerkiksi pienemmän kolmion pisimmän sivun $OB$ pituus voidaan selvittää verrantoyhtälön avulla seuraavasti:
Merkitään sivun $OB$ pituutta kirjaimella $x$. Muodostetaan sen suhde vastinsivun $OD$ pituuteen $x + 4$: $$\frac{x}{x+4}.$$ Valitaan jokin toinen kolmion $OAB$ sivu, jonka pituus tunnetaan. Sopiva sivu on $OA$, jonka pituus on $5$. Muodostetaan sen pituuden suhde vastinsivun $OC$ pituuteen: $$\frac{5}{5+3}.$$ Koska kolmiot ovat yhdenmuotoisia, sivun pituuden suhde vastinsivun pituuteen on sama riippumatta siitä, mitä sivua tarkastellaan. Saadaan siis yhtälö $$\frac{x}{x+4} = \frac{5}{8}.$$ Ratkaistaan tämä yhtälö normaaliin tapaan: \begin{align*} \frac{x}{x+4} &= \frac{5}{8} &\quad &\mid \cdot \, (x+4) \\[1mm] x &= \frac{5}{8}(x+4) &\quad &\mid \cdot \, 8 \\[1mm] 8x &= 5(x+4) & & \\ 8x &= 5x + 20 &\quad &\mid -5x \\ 3x &= 20 &\quad &\mid \, : 3 \\[1mm] x &= \frac{20}{3} \end{align*} Sivun $OB$ pituus on siis $\frac{20}{3} = 6\frac{2}{3}$.
Kolmioiden yhdenmuotoisuus

Tarkastellaan edelleen yllä olevaa kuvaa, jossa kolmiot $OAB$ ja $OCD$ ovat yhdenmuotoisia. Selvitä sivun $AB$ pituus verrantoyhtälön avulla samaan tapaan kuin edellä tehtiin.
VASTAUS
Sivun $AB$ pituus on $\frac{15}{4} = 3{,}75$.
Kolmioiden yhdenmuotoisuus
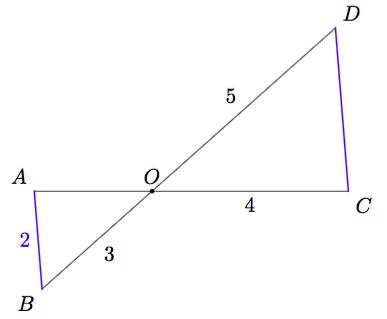
Yllä olevassa kuvassa janat $AB$ ja $CD$ ovat yhdensuuntaisia eli $AB \parallel CD$.
- Palauta mieleesi, mitä tarkoitetaan ristikulmilla ja samankohtaisilla kulmilla (tehtävät 1.6 & 1.7 sekä niiden välinen teksti).
- Selitä omin sanoin, mistä syystä kolmiot $OAB$ ja $OCD$ ovat yhdenmuotoisia.
Vinkki: KK-lause (teoreema 3) sekä edellinen kohta. - Selvitä janan $CD$ pituus sopivan verrantoyhtälön avulla. Arvioi kuvan avulla, onko tuloksesi järkevä.
- Selvitä janan $OA$ pituus sopivan verrantoyhtälön avulla. Arvioi kuvan avulla, onko tuloksesi järkevä.
VASTAUS
- Janan $CD$ pituus on $\frac{10}{3} = 3\frac{1}{3}$.
- Janan $OA$ pituus on $\frac{12}{5} = 2{,}4$.
Suorakulmainen kolmio
Suorakulmainen kolmio tarkoittaa kolmiota, jonka yksi kulma on suora kulma eli $90^\circ$. Esimerkiksi alla oleva kolmio on suorakulmainen kolmio.
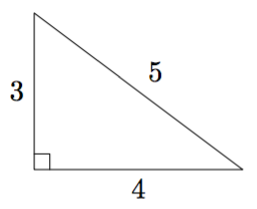
Suorakulmaisen kolmion pisintä sivua sanotaan hypotenuusaksi ja lyhyempiä sivuja kateeteiksi. Esimerkiksi yllä olevan kolmion hypotenuusan pituus on 5 ja kateettien pituudet ovat 3 ja 4.
Tutkitaan seuraavaksi, miten suorakulmaisen kolmion hypotenuusan pituus ja kateettien pituudet liittyvät toisiinsa.
Suorakulmaiset kolmiot
- Neljä samanlaista suorakulmaista kolmiota asetellaan neliön muotoon kuten alla olevassa kuvassa. Miten voidaan päätellä, että keskelle jäävän valkoisen nelikulmion kaikki kulmat ovat suoria kulmia?
Vihje: teoreema 2.
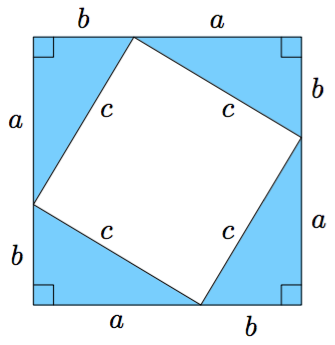
- Muodosta lauseke ylläolevan valkoisen neliön pinta-alalle.
- Samat suorakulmaiset kolmiot järjestetään uudelleen kuten alla olevassa kuvassa. Muodosta lauseke valkoisen alueen pinta-alalle.
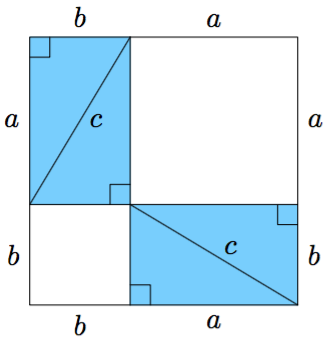
- Vertaa b- ja c-kohtien tuloksia. Millaisen yhtälön saat suorakulmaisen kolmion kateettien pituuksien ja hypotenuusan pituuden välille?
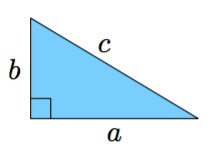
TEOREEMA
Suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö, eli alla olevan kuvan merkinnöillä $$a^2 + b^2 = c^2$$

Seuraavissa tehtävissä harjoitellaan Pythagoraan lauseen soveltamista.
Pythagoraan lause
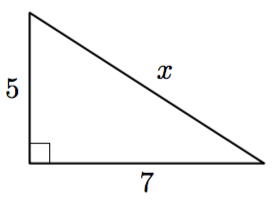
Tehtävänä on selvittää yllä olevan kolmion kolmannen sivun pituus.
- Muodosta kolmion sivujen pituuksien välille Pythagoraan lauseen mukainen yhtälö. Ratkaise tästä yhtälöstä tuntemattoman sivun pituuden neliö eli $x^2$.
- Edellisessä kohdassa olet päätynyt niin sanottuun toisen asteen potenssiyhtälöön $x^2 = s$, joita ratkaistiin edellisessä kurssissa. Jos vakio $s$ on positiivinen eli $s > 0$, tällä yhtälöllä on kaksi ratkaisua. Mitkä nämä ratkaisut ovat a-kohdan yhtälön tapauksessa? Selitä omin sanoin, miksi vain toinen niistä voi olla kysytty kolmion sivun pituus.
- Mikä on yllä olevan kolmion kolmannen sivun pituus? Anna vastauksen tarkka arvo ja likiarvo kahden merkisevän numeron tarkkuudella.
VASTAUS
- $x = \sqrt{74} \approx 8{,}6$.
Pythagoraan lause
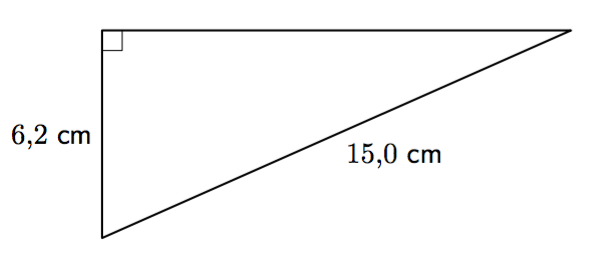
Tehtävänä on selvittää yllä olevan kolmion kolmannen sivun pituus.
- Merkitse tuntemattoman sivun pituutta jollakin kirjaimella. Muodosta kolmion sivujen pituuksien välille Pythagoraan lauseen mukainen yhtälö. Ratkaise tästä yhtälöstä tuntemattoman sivun pituuden neliö.
- Edellisessä kohdassa olet jälleen päätynyt niin sanottuun toisen asteen potenssiyhtälöön. Ratkaise tästä yhtälöstä tuntemattoman sivun pituus. Anna vastaus kahden merkisevän numeron tarkkuudella.
VASTAUS
- Noin 14 cm.
Pythagoraan lause
Hissin oviaukon korkeus on 2,00 metriä ja leveys 0,60 metriä. Hissikorin pituus oviaukosta peräseinään on 1,40 metriä. Tehtävänä on selvittää, mahtuuko 2,05 m pitkä ja 1,00 m leveä pöytälevy ovesta hissiin sopivasti kallistettuna.
- Piirrä kuva hissin oviaukosta edestäpäin katsottuna. Merkitse piirrokseen oviaukon mitat.
- Missä asennossa pöytälevy kannattaa siirtää hissiin? Täydennä piirrosta ja merkitse pöytälevyn suurinta mahdollista pituutta jollakin kirjaimella.
- Muodosta sopiva yhtälö ja ratkaise pöytälevyn suurin mahdollinen pituus.
- Mahtuuko 2,05 m pitkä ja 1,00 m leveä pöytälevy ovesta hissiin?
VASTAUS
- Hissiin mahtuvan pöytälevyn suurin mahdollinen pituus on $\sqrt{4{,}36} \text{ cm} \approx 2{,}09 \text{ cm}$.
- Teoriassa pitäisi mahtua.
Pythagoraan lause
Hissin oviaukon korkeus on 2,00 metriä ja hissikorin pituus oviaukosta peräseinään on 1,40 metriä. Tehtävänä on selvitää, mikä hissin oven leveyden pitäisi vähintään olla, jotta 2,30 m pitkä ja 1,20 metriä leveä kipsilevy mahtuisi hissiin.
- Piirrä kuva hissin oviaukosta edestäpäin katsottuna. Merkitse piirrokseen oviaukon mitat. Merkitse oviaukon leveyttä jollakin kirjaimella.
- Missä asennossa kipsilevy kannattaa siirtää hissiin? Täydennä piirrosta ja merkitse siihen kipsilevyn mitta.
- Muodosta sopiva yhtälö ja ratkaise hissin oven leveys. Mikä on järkevä tarkkuus vastaukselle?
VASTAUS
- Oven vähimmäisleveys on $\sqrt{1{,}29} \text{ m} \approx 1{,}14 \text{ m}$.
Pythagoraan lauseen avulla saadaan aina ratkaistua suorakulmaisen kolmion kolmas sivu, jos kahden sivun pituus tunnetaan. Tutkitaan seuraavaksi, miten voidaan selvittää suorakulmaisen kolmion terävien kulmien suuruus, jos sivujen pituudet tunnetaan.
Tarkastellaan kahta suorakulmaista kolmiota, joissa on yhtä suuri terävä kulma $\alpha$.
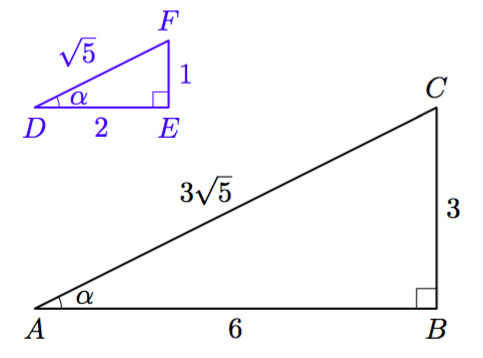
Nämä kolmiot ovat yhdenmuotoiset KK-lauseen (teoreema 3) nojalla, koska niissä on kaksi yhtä suurta kulmaa: suora kulma sekä kulma $\alpha$.
Koska kolmiot ovat yhdenmuotoiset, on suhde $$\frac{\text{ vastinsivun pituus }}{\text{ sivun pituus }}$$ sama riippumatta siitä, mitä kolmion sivua tarkastellaan. Esimerkiksi $$\frac{AB}{\textcolor{blue}{DE}} = \frac{6}{2} = 3$$ ja $$\frac{AC}{\textcolor{blue}{DF}} = \frac{3\sqrt{5}}{\sqrt{5}} = 3.$$ Verrantoyhtälön $$\frac{AB}{\textcolor{blue}{DE}} = \frac{AC}{\textcolor{blue}{DF}}$$ molemmat puolet voidaan kertoa nimittäjien tulolla $\textcolor{blue}{DE} \cdot \textcolor{blue}{DF}$, jolloin saadaan yhtälö $$AB \cdot \textcolor{blue}{DF} = AC \cdot \textcolor{blue}{DE}.$$ Kun tämän yhtälön molemmat puolet jaetaan tulolla $AC \cdot \textcolor{blue}{DF}$, saadaan yhtälö $$\frac{AB}{AC} = \frac{\textcolor{blue}{DE}}{\textcolor{blue}{DF}}.$$ Havaitaan, että kolmion $ABC$ sivujen suhde on sama kuin niiden vastinsivujen suhde kolmiossa $DEF$.

Esimerkiksi edellä tarkasteltu kulman $\alpha$ viereisen kateetin suhde hypotenuusaan on molemmissa kolmioissa sama $$\frac{6}{3\sqrt{5}} = \frac{2}{\sqrt{5}} = \frac{2}{5}\sqrt{5}.$$
Suorakulmaisen kolmion sivujen pituuksien suhteille onkin annettu omat nimensä seuraavan määritelmän mukaisesti:
MÄÄRITELMÄ: SINI, KOSINI JA TANGENTTI
Suorakulmaisessa kolmiossa terävän kulman $\alpha$ sini, kosini ja tangetti tarkoittavat kolmion sivujen pituuksien suhteita: \begin{align*} \sin \alpha &= \dfrac{\text{ kulman vastainen kateetti }}{\text{ hypotenuusa }} \\[2mm] \cos \alpha &= \dfrac{\text{ kulman viereinen kateetti }}{\text{ hypotenuusa }} \\[2mm] \tan \alpha &= \dfrac{\text{ kulman vastainen kateetti }}{\text{ kulman viereinen kateetti }} \end{align*}
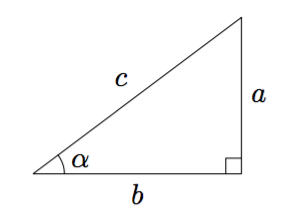
Yllä olevan kuvion merkinnöillä \begin{align*} \sin \alpha &= \dfrac{a}{c} \\[1mm] \cos \alpha &= \dfrac{b}{c} \\[1mm] \tan \alpha &= \dfrac{a}{b} \end{align*}
TRIGONOMETRISET SUHTEET
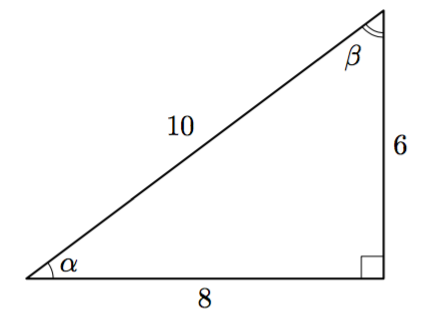
Suorakulmaisen kolmion hypotenuusan pituus on 10 ja kateettien pituudet ovat 6 ja 8 yllä olevan kuvan mukaisesti. Määritä seuraavat sivujen suhteet:
- $\sin \alpha$
- $\cos \alpha$
- $\tan \alpha$
- $\sin \beta$
- $\cos \beta$
- $\tan \beta$
VASTAUS
- $\sin \beta = \dfrac{4}{5}$
- $\cos \beta = \dfrac{3}{5}$
- $\tan \beta = \dfrac{4}{3}$
TRIGONOMETRISET SUHTEET
Suorakulmaisessa kolmiossa terävän kulman $\alpha$ tangetti on $5:12$ eli $$\tan \alpha = \frac{5}{12}$$
- Keksi esimerkki suorakulmaisesta kolmiosta, jossa on tällainen terävä kulma. Mitkä ovat keksimäsi suorakulmaisen kolmion kateettien pituudet?
- Laske keksimäsi suorakulmaisen kolmion hypotenuusan pituus.
- Keksi esimerkki toisesta suorakulmaisesta kolmiosta, jossa on samanlainen kulma $\alpha$. Selitä omin sanoin, miten ajattelit.
TRIGONOMETRISET SUHTEET
Tarkastele alla olevaa neliötä, joka on jaettu lävistäjällä kahdeksi suorakulmaiseksi kolmioksi.
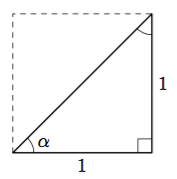
- Laske suorakulmaisen kolmion hypotenuusan pituus.
- Päättele kulman $\alpha$ suuruus kolmion symmetrian avulla.
Vihje: teoreema 2. - Määritä kolmion sivujen pituuksien avulla $\sin \alpha$, $\cos \alpha$ ja $\tan \alpha$.
Edellisen tehtävän perusteella voidaan laatia seuraava taulukko:
| Kulma $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ |
| $45^\circ$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{\sqrt{2}}$ | $1$ |
Jokaista terävää kulmaa vastaa yksi sinin, kosinin ja tangentin arvo. Esimerkiksi yllä olevasta taulukosta nähdään, että $$\cos 45^\circ = \dfrac{1}{\sqrt{2}}.$$
Toisaalta jokaista (suorakulmaisessa kolmiossa mahdollista) trigonometristä suhdetta vastaa yksi terävä kulma. Esimerkiksi yllä olevan taulukon avulla voidaan päätellä, että jos $\tan \beta = 1$, niin $\beta = 45^\circ$.
Laskinten ja tietokoneiden avulla tämä siirtyminen kulman ja trigonometristen suhteiden välillä voidaan tehdä ilman taulukoiden käyttöä. Annettua kulmaa vastaava trigonometrinen suhde sini, kosini tai tangentti saadaan laskimella käyttämällä nappulaa $\bbox[3px,border:2px solid black]{\texttt{sin}\phantom{i}}\ $, $\ \bbox[3px,border:2px solid black]{\texttt{cos}\phantom{i}}\ $ tai $\ \bbox[3px,border:2px solid black]{\texttt{tan}\phantom{i}}\ $. Trigonometrista suhdetta vastaava kulma saadaan nappuloilla $\bbox[3px,border:2px solid black]{\texttt{sin}^{-1}}\ $, $\ \bbox[3px,border:2px solid black]{\texttt{cos}^{-1}}\ $ ja $\ \bbox[3px,border:2px solid black]{\texttt{tan}^{-1}}\ $.
KULMAT JA TRIGONOMETRISET SUHTEET
Kopioi alla oleva taulukko vihkoosi ja täydennä siihen puuttuvat tiedot laskimen avulla tarkkoina arvoina tai kolmen merkitsevän numeron tarkkuudella:
| Kulma $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ |
| $10^\circ$ | $\phantom{\dfrac{1}{2}}$ | ||
| $\dfrac{1}{2}$ | |||
| $\dfrac{1}{\sqrt{2}}$ | |||
| $\phantom{\dfrac{1}{2}}$ | $\sqrt{3}$ | ||
| $80^\circ$ | $\phantom{\dfrac{1}{2}}$ |
KULMAT JA TRIGONOMETRISET SUHTEET
Tarkastele alla olevaa suorakulmaista kolmiota.
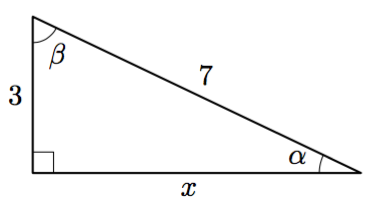
- Selvitä toisen kateetin pituus (tarkka arvo).
- Selvitä kulman $\alpha$ suuruus jonkin trigonometrisen suhteen avulla. Anna vastaus kolmen merkitsevän numeron tarkkuudella.
- Selvitä kulman $\beta$ suuruus.
VASTAUS
- $\sqrt{40} = 2\sqrt{10}$
- $\alpha \approx 25{,}4^\circ$
- $\beta \approx 64{,}6^\circ$
KULMAT JA TRIGONOMETRISET SUHTEET
Tarkastele alla olevaa suorakulmaista kolmiota.
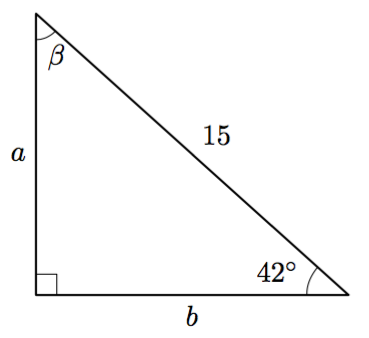
- Ilmaise $\sin 42^\circ$ kolmion sivujen suhteena. Ratkaise tästä yhtälöstä kateetin $a$ pituus kolmen merkitsevän numeron tarkkuudella.
- Ilmaise $\cos 42^\circ$ kolmion sivujen suhteena. Ratkaise tästä yhtälöstä kateetin $b$ pituus kolmen merkitsevän numeron tarkkuudella.
- Selvitä kulman $\beta$ suuruus.
VASTAUS
- $a \approx 10{,}0$
- $b \approx 11{,}1$
- $\beta = 48^\circ$
KULMAT JA TRIGONOMETRISET SUHTEET
Laskettelurinteen pituus on 1300 metriä ja korkeusero 262 metriä. Tehtävänä on laskea mäen rinteen keskimääräinen kaltevuuskulma (vaakatasoon verrattuna).
- Piirrä mallikuva, jossa rinteen poikkileikkaus sivusta katsottuna on suorakulmainen kolmio. Merkitse kuvaan rinteen mitat.
- Ratkaise rinteen kaltevuuskulma sopivan trigonometrisen suhteen avulla. Anna vastaus kahden merkitsevän numeron tarkkuudella.
VASTAUS
- Rinteen kaltevuuskulma on noin 12 astetta.
Tylpän kulman kosini ja sini
Edellisessä kappaleessa määriteltiin terävän kulman kosini ja sini suorakulmaisen kolmion sivujen pituuksien suhteina. Tässä kappaleessa otetaan käyttöön määritelmä, joka sopii kaikille kulmille nollakulmasta oikokulmaan.
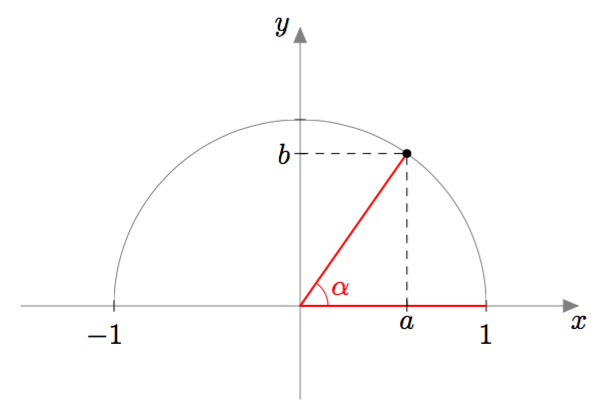
Tarkastellaan kulmaa $\alpha$, joka on välillä $[0^\circ, 180^\circ]$. Merkitään tämä kulma koordinaatistoon kuten alla olevassa kuvassa: piirretään origosta lähtevä jana, joka muodostaa positiivisen $x$-akselin kanssa kulman $\alpha$ ja jonka pituus on $1$.
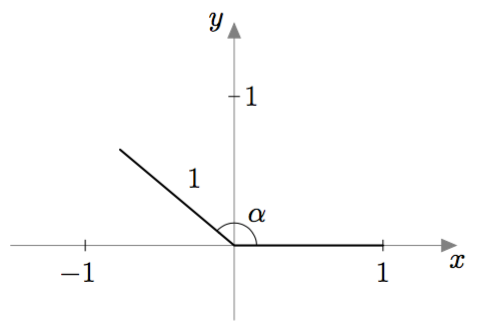
Kulman $\alpha$ kosini ja sini saadaan määriteltyä näin piirretyn janan toisen päätepisteen avulla.
MÄÄRITELMÄ: KOSINI JA SINI
Oletetaan, että $0^\circ \leq \alpha \leq 180^\circ$. Piirretään origosta lähtevä jana, joka muodostaa positiivisen $x$-akselin kanssa kulman $\alpha$ ja jonka pituus on $1$.
- Kulman $\alpha$ kosini on tämän janan toisen päätepisteen $x$-koordinaatti.
- Kulman $\alpha$ sini on tämän janan toisen päätepisteen $y$-koordinaatti.
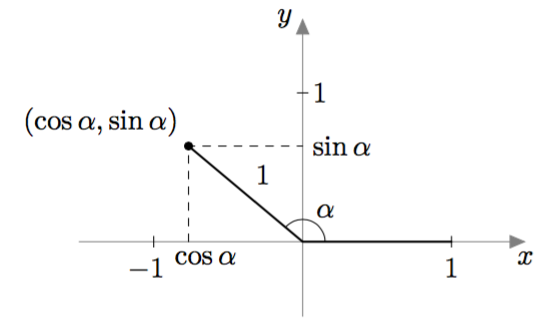
Seuraavassa tehtävässä tarkistetaan, ettei yllä oleva uusi määritelmä ole terävien kulmien tapauksessa ristiriidassa vanhan määritelmän kanssa.
KOSINI JA SINI
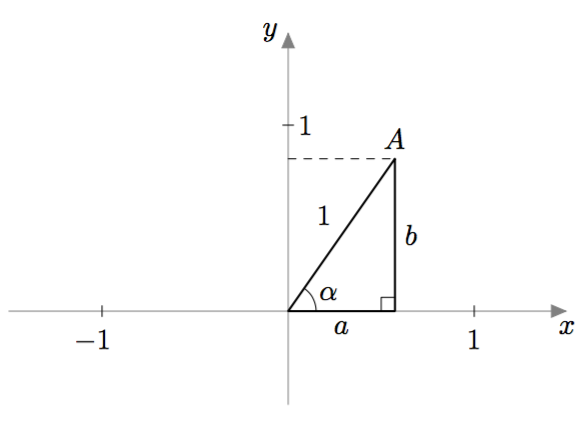
Yllä olevassa kuvassa terävä kulma $\alpha$ on merkitty koordinaatistoon.
- Ilmaise $\cos \alpha$ ja $\sin \alpha$ kuvassa näkyvän suorakulmaisen kolmion sivujen suhteena.
- Ilmaise pisteen $A$ koordinaatit kuvan merkintöjen avulla.
- Vertaa a- ja b-kohtien tuloksia. Ovatko kosinin ja sinin vanha ja uusi määritelmä keskenään sopusoinnussa?
Kun erilaisia kulmia nollakulman ja oikokulman väliltä merkitään koordinaatistoon, muodostavat niiden kylkien päätepisteet koordinaatistoon origokeskisen puoliympyrän, jonka säde on yksi:
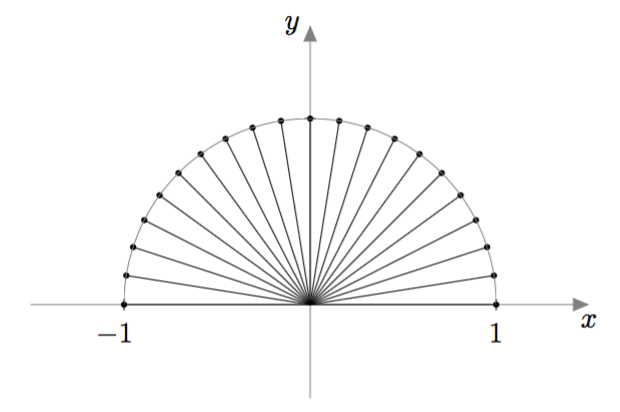
Tämä puoliympyrä on usein tapana piirtää näkyviin, kun tutkitaan erilaisten kulmien kosinin ja sinin ominaisuuksia.
KOSINI JA SINI
Tutki tämän Geogebra-sovelluksen avulla erilaisten kulmien kosinin ja sinin arvoja ja päättele vastaukset seuraaviin kysymyksiin:
- Mitä on $\cos 160^\circ$? Entä $\sin 160^\circ$? Sovelluksesta näet vastaukset kahden desimaalin tarkkuudella.
- Jos kulma $\alpha$ on välillä $[0^\circ, 180^\circ]$, mitä arvoja $\cos \alpha$ voi saada?
- Jos kulma $\alpha$ on välillä $[0^\circ, 180^\circ]$, mitä arvoja $\sin \alpha$ voi saada?
- Mikä ehto kulman $\alpha$ pitää toteuttaa, jotta sen kosini on negatiivinen?
Seuraavissa tehtävissä jatketaan kosinin ja sinin ominaisuuksien tutkimista.
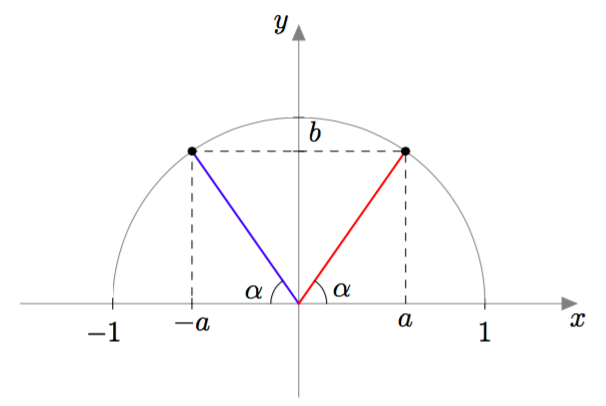
KOSININ OMINAISUUKSIA
Tässä tehtävässä tutkitaan kosinin ominaisuuksia piirrosten avulla.
-
Yllä olevassa kuvassa eräs terävä kulma $\alpha$ on merkitty koordinaatistoon. Ilmaise $\cos \alpha$ kuvan merkinnöillä. - Jos kulman $\alpha$ vasen kylki peilataan $y$-akselin suhteen, syntyy seuraava kuvio:
Sinisellä merkitty jana määrää kulman $\beta$: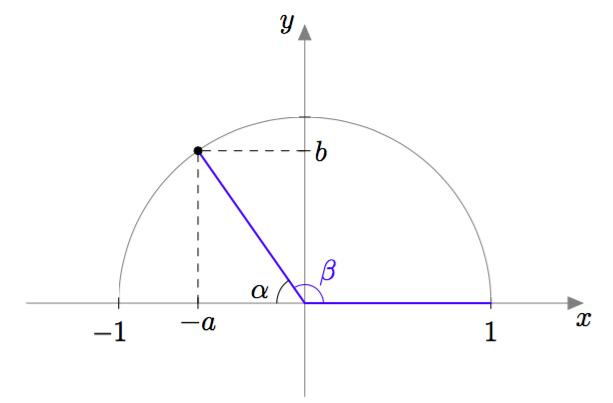
Ilmaise kulma $\beta$ kulman $\alpha$ avulla. Toisin sanottuna, miten saat laskettua kulman $\beta$ suuruuden, jos tiedät kulman $\alpha$? - Ilmaise $\cos \beta$ yllä olevan kuvan merkinnöillä.
- Vertaa a- ja c-kohtien tuloksia ja selitä omin sanoin, miten vieruskulmien $\alpha$ ja $\beta$ kosinien arvot liittyvät toisiinsa.
SININ OMINAISUUKSIA
Tässä tehtävässä tutkitaan sinin ominaisuuksia piirrosten avulla.
-

Yllä olevassa kuvassa eräs terävä kulma $\alpha$ on merkitty koordinaatistoon. Ilmaise $\sin \alpha$ kuvan merkinnöillä. - Jos kulman $\alpha$ vasen kylki peilataan $y$-akselin suhteen, syntyy seuraava kuvio:

Sinisellä merkitty jana määrää kulman $\beta$:
Ilmaise kulma $\beta$ kulman $\alpha$ avulla. Toisin sanottuna, miten saat laskettua kulman $\beta$ suuruuden, jos tiedät kulman $\alpha$? - Ilmaise $\sin \beta$ yllä olevan kuvan merkinnöillä.
- Vertaa a- ja c-kohtien tuloksia ja selitä omin sanoin, miten vieruskulmien $\alpha$ ja $\beta$ sinien arvot liittyvät toisiinsa.
Edellisissä tehtävissä 1.23 ja 1.24 tarkasteltiin kulmaa $\alpha$ ja sen niin sanottua suplementtikulmaa $180^\circ - \alpha$. Näiden tehtävien tuloksista saadaan seuraava teoreema:
TEOREEMA
Kulman ja sen suplementtikulman kosinit ovat toistensa vastalukuja: $$\cos(180^\circ - \alpha) = -\cos \alpha.$$ Kulman ja sen suplementtikulman sinit ovat yhtä suuret: $$\sin(180^\circ - \alpha) = \sin \alpha.$$
TYLPÄN KULMAN KOSINI JA SINI
- Tiedetään, että $$\cos 30^\circ = \frac{\sqrt{3}}{2}$$ ja $$\sin 30^\circ = \frac{1}{2}.$$ Merkitse 30 ja 150 asteen kulmat koordinaatistoon. Päättele piirroksen ja annettujen tietojen avulla ilman laskinta, mitä ovat $\cos 150^\circ$ ja $\sin 150^\circ$.
- Tiedetään, että $$\sin 75^\circ = \frac{1}{4}\left(\sqrt{6}+\sqrt{2}\right).$$ Merkitse 75 asteen kulma koordinaatistoon ja päättele, millä toisella kulmalla on sama sinin arvo.
KULMAN PÄÄTTELEMINEN
- Piirrä koordinaatistoon samanlainen origokeskinen puoliympyrä kuin tehtävässä 1.27 ja merkitse siihen kaikki ne puoliympyrän kehän pisteet, joiden $y$-koordinaatti on 0,75.
- Selvitä laskimen avulla, minkä terävän kulman $\alpha$ sinille pätee $\sin \alpha = 0{,}75$. Anna vastaus asteen kymmenesosan tarkkuudella.
- Määritä a- ja b-kohtien avulla kaikki ne välin $[0^\circ, 180^\circ]$ kulmat, joiden sinin arvo on 0,75.
VASTAUS
- $48{,}6^\circ$ ja $131{,}4^\circ$
KULMAN PÄÄTTELEMINEN
- Piirrä koordinaatistoon samanlainen origokeskinen puoliympyrä kuin edellisessä tehtävässä ja merkitse siihen kaikki ne puoliympyrän kehän pisteet, joiden $x$-koordinaatti on $-0{,}25$.
- Selvitä laskimen avulla, minkä kulman $\alpha$ kosinille pätee $\cos \alpha = -0{,}25$. Anna vastaus asteen kymmenesosan tarkkuudella.
- Määritä a- ja b-kohtien avulla kaikki ne välin $[0^\circ, 180^\circ]$ kulmat, joiden kosinin arvo on $-0{,}25$.
VASTAUS
- $104{,}5^\circ$
Sinilause ja kosinilause
Tässä kappaleessa opitaan selvittämään niin sanottujen vinokulmaisten kolmioiden kulmia ja sivujen pituuksia. Vinokulmaisella kolmiolla tarkoitetaan kolmiota, jossa ei ole yhtään suoraa kulmaa.
Seuraavissa tehtävissä tutkitaan, miten kolmion pinta-ala riippuu kolmion sivuista ja niiden välisestä kulmasta.
KOLMION PINTA-ALA
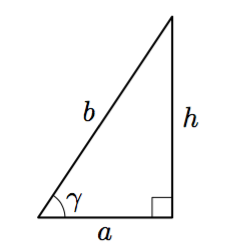
Tehtävänä on näyttää, että yllä olevan kolmion pinta-ala on $$\frac{1}{2}ab\sin \gamma.$$
- Ilmaise $\sin \gamma$ kolmion sivujen suhteena. Ratkaise muodostamastasi yhtälöstä kolmion korkeus $h$.
- Tiedetään, että kolmion pinta-ala on puolet kannan ja korkeuden tulosta eli $$\frac{1}{2}ah.$$ Sijoita tähän a-kohdassa ratkaisemasi korkeuden $h$ lauseke.
KOLMION PINTA-ALA
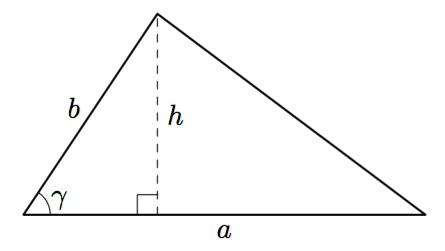
Tehtävänä on tutkia, miten yllä olevan kolmion pinta-ala riippuu kolmion sivuista ja niiden välisestä kulmasta.
- Ilmaise kolmion korkeus $h$ sivun $b$ ja kulman $\gamma$ avulla.
- Yhdistä a-kohdan tulos ja tieto, että kolmion pinta-ala on puolet kannan ja korkeuden tulosta. Millaiseen pinta-alan lausekkeeseen päädyt?
Edellisten tehtävien tulosten avulla saadaan seuraava teoreema:
TEOREEMA
Kolmion pinta-ala on puolet kolmion kahden sivun pituuden ja niiden välisen kulman sinin tulosta: $$\frac{1}{2}ab\sin \gamma$$ 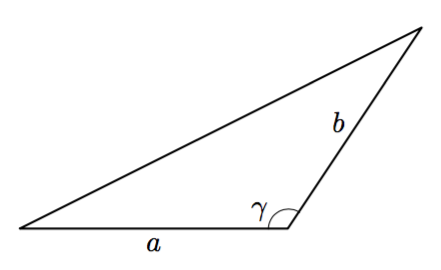
Perustelu: Tiedetään, että kolmion pinta-ala on puolet kannan ja korkeuden tulosta. Kolmion korkeusjanan toinen päätepiste voi sijaita kolmion sivun päätepisteessä, kolmion sivulla tai sivun jatkeella. Tarkastellaan jokainen näistä tapauksista erikseen.
- Tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivun päätepisteessä, on käsitelty tehtävässä 1.31.
- Tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivulla, on käsitelty tehtävässä 1.32.
- Tarkastellaan vielä tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivun jatkeella.

Kolmion korkeus voidaan ratkaista kuvaan piirretystä suorakulmaisesta kolmiosta: $$\frac{h}{b} = \sin(\textcolor{blue}{180^\circ - \gamma}),$$ joten $$h = b\sin(\textcolor{blue}{180^\circ - \gamma}).$$ Edellisessä kappaleessa havaittiin, että kulman ja sen suplementtikulman sini ovat yhtä suuret (teoreema 5), joten $\sin \gamma = \sin(\textcolor{blue}{180^\circ - \gamma})$. Edellinen yhtälö voidaan siten kirjoittaa muodossa $$h = b\sin \gamma.$$ Sijoittamalla tämä kolmion pinta-alan lausekkeeseen saadaan kolmion pinta-alaksi $$\frac{1}{2}ab \sin \gamma.$$
KOLMION PINTA-ALA
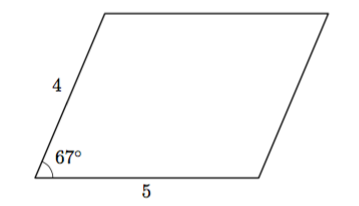
Tehtävänä on laskea yllä olevan suunnikkaan pinta-ala.
- Jaa suunnikas kahdeksi kolmioksi niin, että voit hyödyntää kolmion pinta-alan trigonometristä kaavaa (teoreema 6).
- Laske suunnikkaan pinta-ala. Ilmoita vastaus kolmen merkitsevän numeron tarkkuudella.
VASTAUS
- Suunnikkaan pinta-ala on noin 18,4.
KOLMION PINTA-ALA
Halutaan piirtää kolmio, jonka pinta-ala on 12 cm$^2$ ja jossa on 6 cm ja 8 cm pitkät sivut. Tehtävänä on selvittää, kuinka suuri näiden sivujen välisen kulman $\gamma$ pitää olla.
- Muodosta kolmion pinta-alan trigonometrisen kaavan avulla yhtälö, josta saat ratkaistua, mitä on $\sin \gamma$.
- Selvitä laskimen avulla kulman $\gamma$ suuruus.
- Hahmottele kulma $\gamma$ koordinaatistoon. Päättele piirroksesi avulla, millä tylpällä kulmalla on sama sinin arvo kuin laskimen antamalla terävällä kulmalla.
- Kulma $\gamma$ voidaan siis valita kahdella tavalla. Piirrä näitä vaihtoehtoja vastaavat kolmiot mahdollisimman huolellisesti geokolmion avulla.
VASTAUS
- $30^\circ$
- $150^\circ$
Kolmion pinta-alan trigonometrisen kaavan avulla saadaan perusteltua seuraava teoreema eli niin sanottu sinilause. Sitä voidaan käyttää vinokulmaisen kolmion kulmien ja sivujen pituuksien ratkaisemiseen. Lue teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Jos kolmiosta valitaan mitkä tahansa kaksi sivua ja lasketaan niille suhde $$\dfrac{\text{ sivun pituus }}{\text{ vastaisen kulman sini }}$$ tulokset ovat yhtä suuria. Alla olevan kuvan merkinnöillä siis $$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} \quad \text{ ja } \quad \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$$
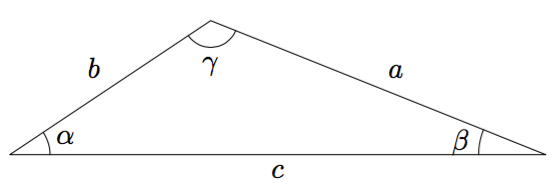
Perustelu: Kolmion pinta-ala on puolet kolmion kahden sivun pituuden ja niiden välisen kulman sinin tulosta. Yllä olevan kolmion pinta-ala on siis $$\frac{1}{2}bc\sin\alpha$$ tai yhtä hyvin $$\frac{1}{2}ac\sin\beta.$$ Koska kumpikin lauseke kuvaa samaa pinta-alaa, saadaan yhtälö $$\frac{1}{2}bc\sin\alpha = \frac{1}{2}ac\sin\beta.$$ Kun tämän yhtälön molemmat puolet kerrotaan luvulla 2 ja jaetaan sivun pituudella $c \neq 0$, yhtälö saa muodon $$b\sin \alpha = a \sin \beta.$$ Kun tämän yhtälön molemmat puolet jaetaan tulolla $\sin \alpha \sin \beta$, saadaan yhtälö $$\frac{b}{\sin \beta} = \frac{a}{\sin \alpha}.$$ Muut vastaavat yhtälöt saadaan johdettua samaan tapaan.
Seuraavissa tehtävissä harjoitellaan sinilauseen soveltamista.
SINILAUSE
Kolmion yhden sivun pituus on 2,83 m. Tämän sivun viereisten kulmien suuruudet ovat $49{,}5^\circ$ ja $71{,}6^\circ$. Tehtävänä on selvitää kolmion kolmannen kulman suuruus, muiden sivujen pituus sekä kolmion pinta-ala.
- Piirrä tilanteesta mallikuva. Merkitse siihen tiedossa olevat kolmion mitat. Laske kolmion kolmannen kulman suuruus.
- Muodosta sinilauseen avulla yhtälö, jossa esiintyy yksi tuntematon (kolmion jomman kumman tuntemattoman sivun pituus). Ratkaise tämä yhtälö ja anna vastaus kolmen merkitsevän numeron tarkkuudella.
- Selvitä kolmion kolmannen sivun pituus sinilauseen avulla samaan tapaan kuin edellisessä kohdassa.
- Laske kolmion pinta-ala ja anna vastaus kolmen merkitsevän numeron tarkkuudella.
VASTAUS
- Kolmas kulma on $58{,}9^\circ$
- Kolmion muut sivut ovat pituudeltaan noin 3,14 metriä ja noin 2,51 metriä.
- Kolmion pinta-ala on noin $3{,}37 \text{ m}^2$.
SINILAUSE
Laiva kulkee suoraviivaista reittiä nopeudella 22,5 km/h. Auringon laskiessa majakka näkyy kulkusuunnasta $42{,}8^\circ$ oikealle. Tasan 20 minuuttia myöhemmin kulma on $63{,}2^\circ$. Tehtävänä on selvittää, mikä laivan etäisyys majakasta on silloin.
- Laske, miten pitkän matkan laiva kulkee 20 minuutin aikana.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tiedossa olevat mitat.
- Muodosta sinilauseen avulla yhtälö, josta saat ratkaistua kysytyn etäisyyden. Anna vastaus kolmen merkitsevän numeron tarkkuudella.
VASTAUS
- 7,5 km
- Noin 14,6 km.
Seuraava tehtävä osoittaa, että kolmiot, joilla on kaksi yhtä pitkää sivua ja yksi yhtä suuri kulma, voivat kuitenkin olla muuten erilaisia ja sen vuoksi erimuotoisia.
SINILAUSE
Kolmion $ABC$ sivun $AC$ pituus on 6 cm ja sivun $BC$ pituus on 5 cm. Sivun $BC$ vastainen kulma eli kulma $\sphericalangle A$ on suuruudeltaan $52^\circ$. Tehtävänä on selvitää kolmion muiden kulmien suuruus.
- Piirrä tilanteesta kuva seuraavien ohjeiden mukaan:
- Merkitse paperille piste $A$ ja piirrä sen kautta vaakasuora suora.
- Piirrä geokolmion avulla 6 cm pituinen jana, jonka toinen päätepiste on $A$ ja joka muodostaa 52 asteen kulman äsken piirtämäsi vaakasuoran suoran kanssa. Anna tämän janan toiselle päätepisteelle nimeksi $C$.
- Piirrä harpin avulla ympyrä, jonka säde on 5 cm ja jonka keskipiste on $C$. Kuinka monessa pisteessä tämä ympyrä leikkaa pisteen $A$ kautta kulkevan vaakasuoran suoran?
- Ympyrän ja suoran leikkauspisteet sopivat kolmion $ABC$ kulmaksi $B$, sillä niiden etäisyys pisteestä $C$ on 5 cm ja niiden tapauksessa $\sphericalangle A = 52^\circ$. Piirrä näkyviin nämä mahdolliset kolmiot $ABC$.
- Merkitään $\beta = \sphericalangle B$. Muodosta sinilauseen avulla yhtälö, josta saat ratkaistua, mitä on $\sin \beta$. Selvitä sen jälkeen kulman $\beta$ suuruus laskimen avulla. Mikä piirroksesi kulma vastaa laskimen antamaa kulmaa?
- Hahmottele kulma $\beta$ koordinaatistoon ja päättele, millä tylpällä kulmalla on sama sinin arvo kuin laskimen antamalla terävällä kulmalla.
- Laske kolmion kolmannen kulman suuruus molemmissa mahdollisissa tapauksissa.
VASTAUS
- Noin $71^\circ$
- Noin $109^\circ$
- Kolmas kulma on noin $57^\circ$ tai noin $19^\circ$.
Edellisestä tehtävästä huomataan, että jos kolmion kulmia selvitetään sinilauseen avulla, täytyy olla erityisen tarkkana. Koska kulmalla ja sen suplementtikulmalla on aina sama sinin arvo, on mahdollista, että ratkaisuja on kaksi. Se ovatko molemmat ratkaisut todellisuudessa mahdollisia, saadaan selville tarkistamalla, onko kolmion kulmien summa $180^\circ$.
Tiedetään, että jos kolmion sivujen $a$ ja $b$ välinen kulma $\gamma$ on suora kulma, niin Pythagoraan lauseen mukaan $$c^2 = a^2 + b^2.$$ 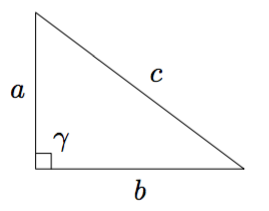
Seuraavaksi tutkitaan, onko kolmion sivujen pituuksilla jokin samantyyppinen yhteys myös vinokulmaisten kolmioiden tapauksessa.
KOLMION SIVUJEN PITUUDET
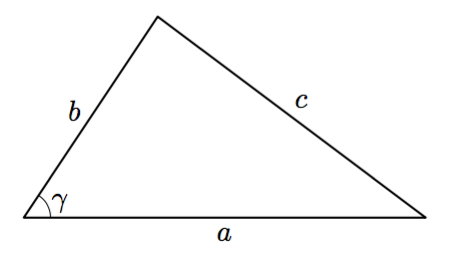
Tässä tehtävässä tutkitaan yllä olevaa kolmiota. Tehtävänä on muodostaa yhteys kolmion sivujen $a$, $b$ ja $c$ sekä kulman $\gamma$ välille.
- Kun kolmiolle piirretään korkeusjana, kolmion kanta jakautuu kahteen osaan. Merkitään niistä vasemmanpuoleisen pituutta kirjaimella $x$, kuten alla olevassa kuvassa. Tällöin oikeanpuoleisen osan pituus on $a-x$.
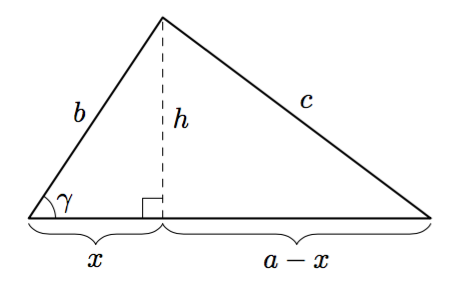
Ilmaise korkeuden neliö $h^2$ kahdella erilaisella tavalla soveltamalla Pythagoraan lausetta kumpaankin kuvassa näkyvään suorakulmaiseen kolmioon. - Yhdistä a-kohdan tulokset yhtälöksi ja muokkaa tämä yhtälö muotoon $$c^2 = a^2 + b^2 - 2ax.$$
- Ilmaise osan $x$ pituus sivun $b$ ja kulman $\gamma$ avulla sopivaa trigonometristä suhdetta käyttäen. Sijoita tämä lauseke c-kohdan yhtälöön. Millaiseen yhtälöön päädyt?
Edellisessä tehtävässä perusteltiin niin sanottu kosinilause terävän kulman tapauksessa. Seuraavassa tehtävässä tarkistetaan, onko kosinilause voimassa myös suorakulmaisessa kolmiossa.
KOLMION SIVUJEN PITUUDET

Tässä tehtävässä tutkitaan, päteekö yhtälö $$c^2 = a^2 + b^2 - 2ab\cos \gamma$$ myös yllä olevan suorakulmaisen kolmion tapauksessa.
- Piirrä 90 asteen kulma koordinaatistoon ja päättele, mitä on $\cos 90^\circ$. Tarkista laskimella.
- Sijoita a-kohdan tulos yhtälöön $$c^2 = a^2 + b^2 - 2ab\cos \gamma.$$ Millaiseen yhtälöön päädyt? Mistä tiedät, että tämä yhtälö toteutuu yllä olevan suorakulmaisen kolmion tapauksessa?
Edellisten tehtävien tulosten avulla saadaan seuraava teoreema eli niin sanottu kosinilause. Sitä voidaan käyttää vinokulmaisen kolmion kulmien ja sivujen pituuksien ratkaisemiseen niissä tapauksissa, joissa sinilauseesta ei ole hyötyä. Lue teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Jos $a$ ja $b$ ovat kolmion kaksi sivua, $\gamma$ niiden välinen kulma sekä $c$ kolmion kolmas (kulman $\gamma$ vastainen) sivu, niin $$c^2 = a^2 + b^2 - 2ab\cos \gamma.$$

Perustelu: Tarkasteltavan kolmion korkeusjanan toinen päätepiste voi sijaita kolmion sivulla, sivun päätepisteessä tai sivun jatkeella. Tarkastellaan jokainen näistä tapauksista erikseen.
- Tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivulla, on käsitelty tehtävässä 1.38.
- Tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivun päätepisteessä, on käsitelty tehtävässä 1.39.
- Tarkastellaan vielä tapaus, jossa kolmion korkeusjanan toinen päätepiste sijaitsee kolmion sivun jatkeella.

Korkeuden neliö $h^2$ voidaan ratkaista pienestä suorakulmaisesta kolmiosta Pythagoraan lauseella: $$h^2 = b^2-x^2.$$ Se voidaan ratkaista myös isommasta suorakulmaisesta kolmiosta samaan tapaan: $$h^2 = c^2 - (a+x)^2.$$ Yhdistämällä nämä tulokset saadaan yhtälö $$c^2 - (a+x)^2 = b^2-x^2.$$ Kun käytetään summan neliön kaavaa tai kerrotaan sulut auki lausekkeesta $(a+x)^2$, saadaan yhtälö muotoon $$c^2-(a^2+2ax + x^2) = b^2 - x^2.$$ Kun huomioidaan miinusmerkin vaikutus, saadaan yhtälö muotoon $$c^2 - a^2 - 2ax - x^2 = b^2 - x^2.$$ Kun lisätään tämän yhtälön molemmille puolille $a^2 + 2ax + x^2$, saadaan yhtälö $$c^2 = a^2 + b^2 + 2ax.$$
Pienemmästä suorakulmaisesta kolmiosta voidaan nyt ratkaista $x$: $$\frac{x}{b} = \cos(\textcolor{blue}{180^\circ - \gamma}),$$ joten $$x = b\cos(\textcolor{blue}{180^\circ - \gamma}).$$ Edellisessä kappaleessa havaittiin, että kulman ja sen suplementtikulman kosini ovat toistensa vastaluvut (teoreema 5), joten $\cos(\textcolor{blue}{180^\circ - \gamma}) = -\cos \gamma$. Siten $$x = -b\cos\gamma.$$ Kun tämä sijoitetaan edellä johdettuun yhtälöön, saadaan yhtälö $$c^2 = a^2 + b^2 - 2ab\cos \gamma.$$
Seuraavissa tehtävissä harjoitellaan kosinilauseen soveltamista.
KOSINILAUSE
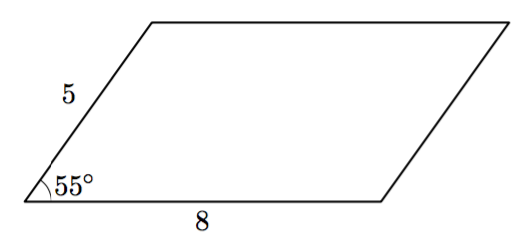
Tehtävänä on laskea yllä olevan suunnikkaan lävistäjien pituudet.
- Merkitse alla olevassa kuvassa näkyvää lävistäjää jollakin kirjaimella ja ratkaise sen pituus kosinilauseen avulla. Anna vastaus kolmen merkitsevän numeron tarkkuudella.
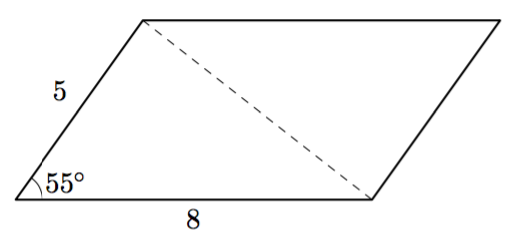
- Päättele alla olevaan kuvaan merkityn kulman $\gamma$ suuruus.
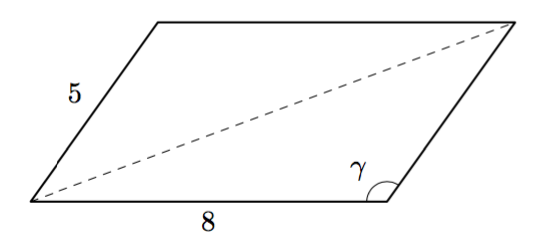
Vinkki: vieruskulmat ja samankohtaiset kulmat. - Ratkaise suunnikkaan toisen lävistäjän pituus.
VASTAUS
- Lävistäjän pituus on noin 6,57.
- $125^\circ$
- Toisen lävistäjän pituus on noin 11,6.
KOSINILAUSE
Kolmion sivujen pituudet ovat 3 cm, 5 cm ja 7 cm. Tehtävänä on laskea kolmion suurimman kulman suuruus.
- Päättele, mikä kolmion suurimman kulman vastaisen sivun pituus. Selitä omin sanoin, miten ajattelit.
- Piirrä kolmiosta mahdollisimman tarkka kuva seuraavien ohjeiden mukaan:
- Piirrä 7 cm pitkä vaakasuora jana.
- Piirrä harpilla ympyrä, jonka keskipiste on janan vasen päätepiste ja säde 3 cm.
- Piirrä harpilla ympyrä, jonka keskipiste on janan oikea päätepiste ja säde 5 cm.
- Ympyröiden leikkauspisteet sopivat kolmion kolmanneksi kärjeksi, sillä niiden etäisyys janan kummastakin päätepisteestä on sopiva. Valitse toinen leikkauspisteistä ja piirrä kolmio näkyviin.
- Ratkaise kolmion suurimman kulman suuruus kosinilauseen avulla.
Vinkki: Ratkaise ensin kulman kosinin arvo. Määritä sen jälkeen kulman suuruus laskimen avulla.
VASTAUS
- Kolmion suurin kulma on $120^\circ$.
KOSINILAUSE
Riian satamasta lähtenyt laiva on purjehtinut ensin 133 km luoteeseen ja sen jälkeen 80 km länteen. Tehtävänä on laskea, miten kaukana laiva on satamasta.
- Tarkista tarvittaessa ilmansuuntien nimitysten merkitys esimerkiksi netistä.
- Piirrä tilanteesta mallikuva. Merkitse siihen kaikki tunnetut etäisyydet ja kulmat, jotka voidaan päätellä ilmansuuntien avulla.
- Miten kaukana laiva on satamasta? Anna vastaus kahden merkitsevän numeron tarkkuudella.
VASTAUS
- Laivan etäisyys satamasta on noin 200 km.
KOSINILAUSE
Kolmion sivujen pituudet ovat $4$, $3$ ja $\sqrt{7}$.
- Piirrä kolmio harpin ja viivottimen avulla. Katso tarvittaessa ohjeita tehtävästä 1.41.
- Kokeile, toteuttaako tämä kolmio Pythagoraan lauseen yhtälön $c^2 = a^2 + b^2$.
- Selvitä kolmion suurimman kulman suuruus kosinilauseen avulla.
VASTAUS
- Suurin kulma on $90^\circ$.
Edellisen tehtävän havainnot voidaan yleistää: Jos kolmion kahden sivun neliöiden summa on sama kuin kolmannen sivun neliö, niin kolmio on suorakulmainen. Lue teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Jos kolmion sivut $a$, $b$ ja $c$ toteuttavat yhtälön $c^2 = a^2 + b^2$, niin sivujen $a$ ja $b$ välinen kulma on suora kulma.
Perustelu: Kosinilauseen mukaan $$c^2 = a^2 + b^2 - 2ab\cos \gamma,$$ missä $\gamma$ on sivujen $a$ ja $b$ välinen kulma. Koska oletuksen mukaan $c^2 = a^2 + b^2$, voidaan päätellä, että $$2ab\cos\gamma = 0.$$ Sivujen pituudet $a$ ja $b$ ovat positiivisia, joten tulon nollasäännöstä seuraa, että $\cos \gamma = 0$. Ainoa välin $[0^\circ, 180^\circ]$ kulma, jonka kosini on nolla, on suora kulma. Siis $\gamma = 90^\circ$.
PYTHAGORAAN LAUSEEN KÄÄNTEISLAUSE
Kolmion sivujen pituudet ovat $2\sqrt{2}$, $6$ ja $2\sqrt{7}$.
- Miten voit päätellä ilman laskinta, mikä on kolmion pisin sivu?
- Osoita, että kolmio on suorakulmainen.
VINKKI
- Tutki sivujen pituuksien neliöitä eli toisia potensseja.
- Teoreema 9.
TEHTÄVÄSARJA II
Kolmion pinta-ala
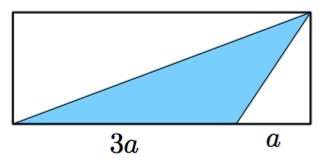
Halutaan piirtää kolmio, jonka korkeus on kolminkertainen kantaan verrattuna ja jonka pinta-ala on 24 cm$^2$.
- Piirrä tilanteesta mallikuva. Merkitse kolmion kannan pituutta jollakin kirjaimella. Miten saat ilmaistua kolmion korkeuden samaa kirjainta käyttäen?
- Muodosta sopiva yhtälö ja määritä kolmion kannan pituus. Laske sitä vastaava kolmion korkeus.
- Piirrä kaksi erilaista kolmiota, jotka täyttävät tehtävän vaatimukset.
Vastaus
- Olkoon kanta esimerkiksi $a$, jolloin korkeus on $3a$.
- Korkeus 12 cm.
Kolmion pinta-ala
Tasakylkinen kolmio tarkoittaa kolmiota, jossa on kaksi yhtä pitkää sivua. Symmetrian vuoksi tasakylkisen kolmion korkeusjana jakaa kannan kahteen yhtä pitkään osaan ja kantakulmat ovat yhtä suuret.
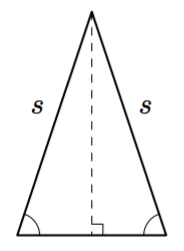
Tiedetään, että tasakylkisen kolmion kanta on puolet kolmion korkeudesta ja että kolmion pinta-ala on 27,0 cm$^2$. Tehtävänä on määrittää kolmion kaikkien sivujen pituudet.
- Piirrä tilanteesta mallikuva. Merkitse kolmion korkeutta jollakin kirjaimella. Miten saat ilmaistua kannan pituuden samaa kirjainta käyttäen?
- Määritä kolmion korkeus ja kannan pituus.
- Määritä kolmion kylkien pituus.
Vastaus
- Olkoon korkeus esimerkiksi $h$, jolloin kanta on $\frac{1}{2}h$.
- Korkeus noin $10{,}4 \text{ cm}$ ja kanta noin $5{,}20 \text{ cm}$.
- Kumpikin kylki noin $10{,}7 \text{ cm}$.
Kulmat
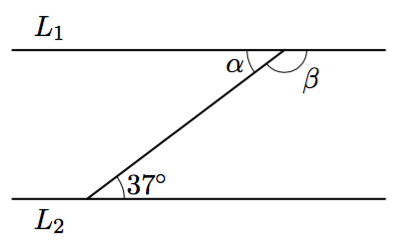
Päättele kulmien $\alpha$ ja $\beta$ suuruudet ja perustele vastauksesi.
-
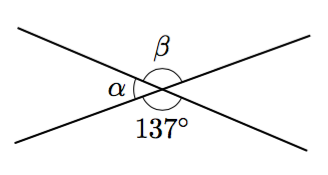
- Suorat $L_1$ ja $L_2$ ovat yhdensuuntaiset.
Vastaus
- $\alpha = 43^\circ$ (vieruskulma) ja $\beta = 137^\circ$ (ristikulma)
- $\alpha = 37^\circ$ (samankohtaiset kulmat) ja $\beta = 143^\circ$ (vieruskulma)
Kulmat
- Päättele kulman $\alpha$ suuruus.
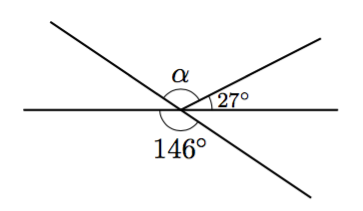
- Päättele kulmien $\beta$, $\gamma$ ja $\delta$ suuruudet
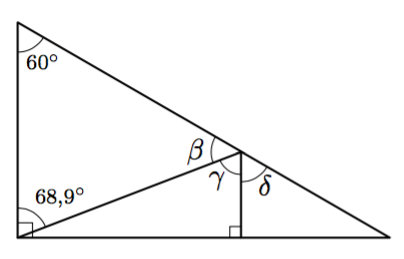
Vastaus
- $\alpha = 119^\circ$ ($\alpha + 27^\circ = 146^\circ$, ristikulmat)
- $\beta = 51{,}1^\circ$ (kolmion kulmien summa), $\delta = 60^\circ$ (samankohtaiset kulmat), $\gamma = 68{,}9^\circ$
Kolmioiden yhdenmuotoisuus
Tasaiselle kentälle pystytetyn lipputangon varjon pituudeksi mitattiin 9,6 metriä. Lipputangon korkeuden määrittämiseksi sen viereen pystytettiin 1,50 metrin pituinen keppi, jonka varjon pituudeksi mitattiin 1,25 metriä.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat.
- Määritä lipputangon korkeus.
Vastaus
- Noin 11,5 metriä.
Kolmioiden yhdenmuotoisuus
Juhlasalin valaisimen etäisyyttä lattiasta arvioitiin pitelemällä sen alla vaakasuorassa 25 cm pituista viivotinta 20 cm etäisyydellä lattiasta. Viivottimen varjoksi mitattiin 27 cm.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat.
- Mikä oli valaisimen etäisyys lattiasta?
Vastaus
- Noin 2,7 metriä.
KOLMIOIDEN YHDENMUOTOISUUS
Suorakulmaisen kolmion kateettien pituus on 6 cm ja 8 cm. Kolmion sisään on piirretty neliö, jonka kaksi sivua on kateeteilla ja yksi kärki hypotenuusalla. Tehtävänä on laskea neliön sivun pituus.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat. Merkitse neliön sivun pituutta jollakin kirjaimella.
- Piirroksessa on näkyvissä kaksi pienempää suorakulmaista kolmiota. Valitse niistä toinen ja ilmaise sen kateettien pituudet ison kolmion kateettien ja neliön sivun pituuden avulla.
- Muodosta sopiva verrantoyhtälö ja ratkaise neliön sivun pituus. Anna tarkka arvo ja likiarvo yhden desimaalin tarkkuudella.
Vastaus
- $\frac{24}{7} \text{ cm} \approx 3{,}4 \text{ cm}$.
SUORAKULMAINEN KOLMIO
Henkilö oli unohtanut avaimet kotiin, mutta muisti jättäneensä yläkerran ikkunan auki. Kun 3,8 m pitkät tikapuut asetettiin ikkunan alareunaa vasten, tikkaiden alapään etäisyydeksi talon seinästä mitattiin 1,4 metriä.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat.
- Kuinka korkealla ikkunan alareuna oli?
- Työterveyslaitos antaa seuraavia ohjeita tikkaiden käyttöön: "Tikkaat, jotka sijoitetaan jyrkempään kuin 70° kulmaan tulee varustaa kaatumisenestolaitteilla. Kaatuminen voidaan estää tikkaan päähän asennettavilla koukuilla tai sitomalla tikkaat rakenteisiin. Tikkaita ei saa myöskään käyttää loivemmassa kuin 60° kulmassa ilman erikoistoimia. Tikkaiden asianmukainen kiinnitys yläpäästä rakenteisiin estää tehokkaasti myös liukumista." Laske tikkaiden kaltevuuskulma tehtävän tilanteessa. Olisiko tässä tilanteessa ollut syytä varautua tikkaiden kaatumiseen tai luisumiseen?
Vastaus
- Noin 3,5 metrin korkeudessa.
- Kaltevuuskulma on noin $68^\circ$, joten erillisiä varotoimenpiteitä ei tarvita.
SUORAKULMAINEN KOLMIO
Seikkailijan pitää vuolaasti virtaava joki liu'ulla, joka on kiinnitetty 30 metriä pitkään vaakasuoraan vaijeriin. Seikkailijan paino venyttää vaijeria, jolloin hän laskeutuu lähemmäs vedenpintaa, alimmilleen vaijerin keskikohdassa. Jos seikkailijan vauhti ei riitä vastarannalle asti, hinaa siellä odottava henkilö hänet perille apuköyden avulla. Vaijerin venymäksi on ilmoitettu enintään 200 kilogramman kuormilla 0,125 %. Tehtävänä on laskea, miten paljon vaijerin keskikohta lasketuu vaakatasosta.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat. Laske myös vaijerin pituus venytettynä.
- Miten paljon vaijerin keskikohta lasketutuu vaakatasoon verrattuna?
- Kuinka korkealle vaakasuora vaijeri pitäisi kiinnittää, jotta seikkailija pääsisi vastarannalle kuivana? Liuku, jolla seikkailija istuu, roikkuu 120 cm vaijerin alapuolella.
Vastaus
- Vaijerin pituus venytettynä 30,0375 metriä.
- Vaijerin keskikohta laskeutuu noin 75 cm.
- Vähintään 1,95 cm korkeudelle veden pinnasta (olettaen, että seikkailija nostaa jalkansa ylös liu'ulla istuessaan).
SUORAKULMAINEN KOLMIO
Kun 2700 mm pitkän ja 50 mm paksun lattialistan toinen pää oli nurkassa samaan tapaan kuin alla olevassa kuvassa, jäi toinen pää vastapäiselle seinälle 35,0 cm korkeudelle. Tehtävänä on selvittää, miten paljon listaa pitää lyhentää.
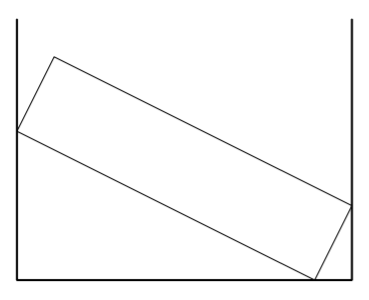
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat.
- Tunnista kuvasta kaksi suorakulmaista kolmiota, joista on apua tehtävän ratkaisemisessa. Ovatko nämä kolmiot yhdenmuotoisia?
- Kuinka paljon listaa pitää lyhentää, jotta se on sopivan mittainen? Anna vastaus millimetrin tarkkuudella.
Vastaus
- Noin 16 mm.
SUORAKULMAINEN KOLMIO
Ranskassa Atlantin rannikolla Saint Malossa vedenpinnan korkeus voi vaihdella nousu- ja laskuveden välillä jopa yli yhdeksän metriä.
- Vesirajan mitattiin siirtyneen rannalla 62 metriä nousu- ja laskuveden välillä, kun ilmoitettu vedenkorkeuden muutos oli 4,31 metriä. Mikä oli rannan keskimääräinen kaltevuuskulma?
- Kuinka paljon vesiraja siirtyy, jos vedenkorkeus muuttuu 9,85 metriä? Oletetaan, että ranta viettää tasaisesti niin, että kaltevuuskulma on likimain vakio.
Vastaus
- Noin $4{,}0^\circ$.
- Kahden merkitsevän numeron tarkkuudella noin 140 metriä.
SUORAKULMAINEN KOLMIO
Sienestäjä kävi tarkastamassa kolme salaista sieniapajaansa kävelemällä metsäautotien päästä ensin 400 m etelään, sitten 950 m itään ja vielä 1 200 m etelään. Tehtävänä on selvittää, mihin kompassisuuntaan hänen pitää kulkea viimeisestä sienipaikasta, jos hän haluaa päästä suoraan takaisin lähtöpaikkaansa mahdollisimman lyhyttä reittiä. Kompassisuunta ilmaistaan asteina pohjoisesta myötäpäivään lukien.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat. Täydennä piirros sopivaksi suorakulmaiseksi kolmioksi.
- Mihin kompassisuuntaan sienestäjän pitää kulkea, jotta hän pääsisi suoraan takaisin lähtöpaikkaansa?
Vastaus
- Kompassisuunta on noin $329^\circ$ eli luoteen ja pohjoisen väliin.
SUORAKULMAINEN KOLMIO
Bengtskärin majakan huipulla seisova henkilö havaitsee suoraan etelässä purjeveneen ja hylkeen. Purjevene näkyy $5^\circ$ ja hylje $25^\circ$ vaakatason alapuolella. Henkilön pää on suunnilleen majakan valon korkeudella eli noin 51 metriä merenpinnan yläpuolella. Tehtävänä on selvittää purjeveneen etäisyys hylkeestä.
- Piirrä mallikuva sekä purjeveneen että hylkeen sijainnista majakkaan verrattuna eli yhteensä kaksi mallikuvaa.
- Mikä on purjeveneen etäisyys majakasta?
- Mikä on purjeveneen etäisyys hylkeestä?
Vastaus
- Purjeveneen etäisyys majakasta on noin 580 metriä.
- Purjeveneen etäisyys hylkeestä on noin 470 metriä.
SUORAKULMAINEN KOLMIO
Autoilijoita saatetaan varoittaa jyrkästä mäestä liikennemerkillä. Merkissä ilmoitetaan mäen kaltevuus suhteena $$\frac{\text{ korkeuden muutos }}{\text{ vaakasuora siirtymä }}$$

- Selvitä mäen kaltevuuskulma asteina yllä olevan liikennemerkin tapauksessa. Muista piirtää mallikuva.
- Lenkkeilijä juoksee mäen rinteen tietä pitkin ja mittaa matkaksi gps-kellonsa avulla 500 metriä. Kuinka korkea mäki tämän perusteella on? Oletetaan, että mäelle nouseva tie ei mutkittele.
Vastaus
- Mäen kaltevuuskulma on noin $4^\circ$.
- Mäen korkeus on noin 35 metriä.
TYLPÄN KULMAN KOSINI JA SINI
Ilmaise pisteen $A$ koordinaatit 152 asteen kulman kosinin ja sinin avulla. Mitkä ovat koordinaattien likiarvot kolmen desimaalin tarkkuudella?
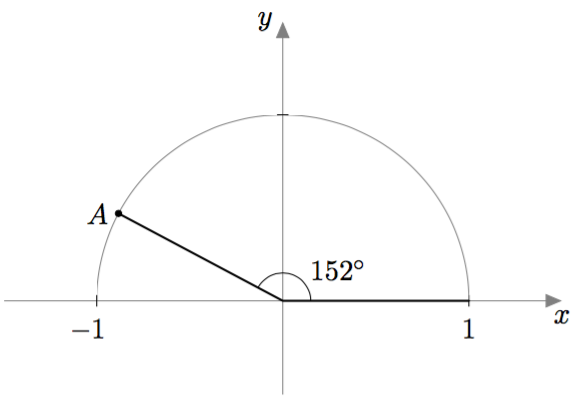
Vastaus
$A = (\cos 152^\circ, \sin 152^\circ) \approx (-0{,}883;\, 0{,}469)$
TYLPÄN KULMAN KOSINI JA SINI
- Merkitse kulma $118^\circ$ koordinaatistoon ja määritä $\cos 118^\circ$ laskimella kolmen desimaalin tarkkuudella. Onko välillä $[0^\circ, 180^\circ]$ olemassa toinen kulma $\alpha$, jonka kosini on yhtä suuri? Jos on, niin mikä?
- Merkitse kulma $165^\circ$ koordinaatistoon ja määritä $\sin 165^\circ$ laskimella kolmen desimaalin tarkkuudella. Onko välillä $[0^\circ, 180^\circ]$ olemassa toinen kulma $\alpha$, jonka sini on yhtä suuri? Jos on, niin mikä?
- Merkitse kulma $78^\circ$ koordinaatistoon ja määritä $\sin 78^\circ$ laskimella kolmen desimaalin tarkkuudella. Onko välillä $[0^\circ, 180^\circ]$ olemassa toinen kulma $\alpha$, jonka sini on yhtä suuri? Jos on, niin mikä?
Vastaus
- $\cos 118^\circ \approx -0{,}469$. Välillä $[0^\circ, 180^\circ]$ ei ole olemassa toista kulmaa, jonka kosini olisi yhtä suuri.
- $\sin 165^\circ \approx 0{,}259$. Myös $\sin 15^\circ = \sin 165^\circ$.
- $\sin 78^\circ \approx 0{,}978$. Myös $\sin 102^\circ = \sin 78^\circ$.
TYLPÄN KULMAN KOSINI JA SINI
Merkitse koordinaatistoon jokin kulma $\alpha$, joka on välillä $[0^\circ, 180^\circ]$, ja sen suplementtikulma $180^\circ - \alpha$. Päättele piirroksesi avulla ilman laskinta kulman $180^\circ - \alpha$ sini ja kosini, jos
- $\sin \alpha = 0{,}8$ ja $\cos \alpha = 0{,}6$
- $\sin \alpha = 0{,}352$ ja $\cos \alpha = -0{,}936$.
Vastaus
- $\sin (180^\circ - \alpha) = 0{,}8$ ja $\cos (180^\circ - \alpha) = -0{,}6$
- $\sin (180^\circ - \alpha) = 0{,}352$ ja $\cos (180^\circ - \alpha) = 0{,}936$.
TYLPÄN KULMAN KOSINI JA SINI
Luonnostele koordinaatistoon kaikki sellaiset kulmat $\alpha$, jotka ovat välillä $[0^\circ, 180^\circ]$ ja joilla
- $\cos \alpha = 0{,}87$
- $\sin \alpha = 0{,}45$
- $\cos \alpha = -0{,}13$
- $\sin \alpha = -0{,}62$.
Määritä kulmien suuruus laskimella asteen kymmenesosan tarkkuudella.
Vastaus
- $\alpha \approx 29{,}5^\circ$
- $\alpha \approx 26{,}7^\circ$ tai $\alpha \approx 153{,}3^\circ$
- $\alpha \approx 97{,}5^\circ$
- Mikään välin $[0^\circ, 180^\circ]$ kulma ei toteuta tätä yhtälöä. Jos kulma on välillä $[0^\circ, 180^\circ]$, sen sinin arvo on aina vähintään nolla.
SINILAUSE JA KOSINILAUSE
Joen leveyttä arvioitiin mittaamalla kahden havaintopisteen välinen etäisyys ja kulmat, joissa vastarannalla oleva kiintopiste näkyi niistä katsottuna.
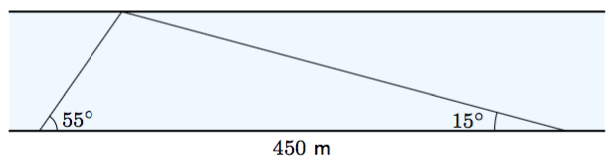
- Ratkaise kolmion jomman kumman tuntemattoman sivun pituus.
- Ratkaise joen leveys.
- Keksi toinen tapa, jolla voisit ratkaista joen leveyden (a-kohdan tulosta saa käyttää). Ratkaise joen leveys tällä tavalla.
Vinkki: teoreemat 1 & 6 tai trigonometriset suhteet.
Vastaus
- Lyhyempi sivu noin 123 m, pitempi sivu noin 392 m.
- Joen leveys kahden merkitsevän numeron tarkkuudella noin 100 metriä.
SINILAUSE JA KOSINILAUSE
Rotkon leveyttä arvioitiin tutkimalla, missä kulmassa rotkon toisella puolella kasvavan männyn latva näkyi. Rotkon reunalta katsottaessa männyn latva näkyi 15 asteen kulmassa vaakatason yläpuolella ja 50 metrin päässä rotkon reunasta kulma oli 9 astetta.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut pituudet ja kulmat. Merkitse rotkon leveyttä jollakin kirjaimella.
- Mitkä piirroksen neljästä tuntemattomasta kulmasta ovat sellaisia, että pystyt päättelemään niiden suuruuden, vaikka sitä ei ole tehtävänannossa kerrottu? Selvitä kaikkien tällaisten kulmien suuruudet.
- Mieti, mitkä kolmioiden sivuista ovat sellaisia, joiden pituus sinun pitää ratkaista, jotta pystyt selvittämään rotkon leveyden. Ratkaise tarvittavien sivujen pituudet. Kuinka leveä rotko on?
Vinkki: teoreema 7 ja sopiva trigonometrinen suhde.
Vastaus
- Noin 72 metriä leveä.
SINILAUSE JA KOSINILAUSE
Kaksi retkeilevää ryhmää havaitsi matalalla lentävän lentokoneen noin klo 15.05. Ensimmäinen ryhmä näki koneen ohittavan heidät lännen puolella noin 30 asteen korkeudessa. Toinen ryhmä huomasi koneen lentävän idässä noin 15 asteen korkeudessa. Kartan mukaan retkikuntien välimatka oli havaintohetkellä noin 8 km.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut pituudet ja kulmat.
- Miten korkealla lentokone lensi havaintohetkellä?
Vinkki: teoreemat 1, 2, 6 & 7.
Vastaus
- Kone lensi noin 1,5 km korkeudessa.
SINILAUSE JA KOSINILAUSE
Kolmion muotoisen metsäpalstan sivujen pituuksiksi mitattiin 1,8 km, 2,1 km ja 3,0 km. Tehtävänä on selvittää palstan pinta-ala.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut mitat.
- Ratkaise kolmion jonkin kulman suuruus. Talleta saamasi tulos laskimen muistiin pyöristämättä sitä.
- Laske metsäpalstan pinta-ala. Käytä laskuissa edellisessä kohdassa laskimen muistiin tallettamaasi kulman tarkkaa arvoa.
Vastaus
- Noin $1{,}9 \text{ km}^2$.
SINILAUSE JA KOSINILAUSE
Pikainen nettihaku kertoo, että Pariisin suurin lentokenttä CDG sijaitsee 20 km Pariisista koilliseen ja noin 67 000 asukkaan kaupunki Bourges sijaitsee 197 km Pariisista etelään linnuntietä mitattuna. Tehtävänä on arvioida näiden tietojen pohjalta, mikä on Bourgesin ja Charles de Gaulle -lentokentän välinen etäisyys linnuntietä pitkin.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut etäisyydet ja pääteltävissä olevat kulmat.
- Arvaa, mikä on Bourgesin ja Charles de Gaulle -lentokentän välinen etäisyys linnuntietä pitkin. Vertaa arvaustasi kaverisi arvaukseen.
- Laske Bourgesin ja Charles de Gaulle -lentokentän välinen etäisyys. Kuinka lähelle arvauksesi osui?
Vastaus
- Noin 212 km.
SINILAUSE JA KOSINILAUSE
Yleisurheilussa esimerkiksi kuulantyönnön tai kiekonheiton pituus voidaan mitata optisesti niin sanotun takymetrin avulla. Paikassa $A$ sijaitseva laite mittaa etäisyyden kuulantyöntö- tai kiekonheittoringin keskipisteeseen $B$ ja putoamispaikkaan $C$ sekä kulman $CAB$. Näistä tiedoista voidaan tietokoneella laskea urheilijan tulos.
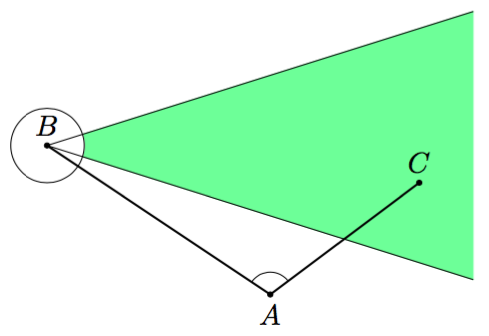
- Keikonheittoringin halkaisija on 2,50 m. Laske heiton pituus tilanteessa, jossa $AB = 35{,}53 \text{ m}$, $AC = 54{,}31 \text{ m}$ ja $\sphericalangle CAB = 97{,}2^\circ$.
- Tietokoneeseen syötetään heittoringin halkaisija $d$, etäisyydet $AB= b$ ja $AC = c$ sekä kulma $\sphericalangle CAB = \alpha$. Ohjelmoijan tehtävä on muodostaa näistä lauseke, joka antaa tuloksena heiton pituuden. Auta ohjelmoijaa ja muodosta lauseke heiton pituudelle.
Vastaus
- 67,27 m
- $\sqrt{b^2+c^2-2bc\cos \alpha} - \frac{d}{2}$
SINILAUSE JA KOSINILAUSE
Mökkien $A$ ja $B$ välinen etäisyys on 1150 m. Mökkien yhteinen laituri rakennetaan paikkaan, jonka etäisyys mökistä $A$ on 800 metriä ja mökistä $B$ 1050 metriä. Mökkejä yhdistävältä suoralta metsätieltä aiotaan rakentaa helppokulkuinen polku laiturille. Tehtävänä on laskea, mikä on tämän polun lyhin mahdollinen pituus eli kuinka etäällä laituri on mökkejä yhdistävästä tiestä.
- Piirrä tilanteesta mallikuva ja merkitse siihen kaikki tunnetut etäisyydet.
- Ratkaise laiturin etäisyys metsätiestä.
- Kuinka pitkä matka mökistä $B$ on laiturille, jos kuljetaan ensin metsätietä ja sitten polkua pitkin?
Vastaus
- Noin 707 m.
- Noin 1480 m.
SINILAUSE JA KOSINILAUSE
Kolmiossa $ABC$ kulman $A$ suuruus on $77^\circ$, sivun $AB$ pituus 5,8 cm ja sivun $BC$ pituus 8,3 cm.
- Piirrä kolmio. Kuinka monta erilaista ehdot täyttävää kolmiota voi piirtää?
- Laske kulmien $B$ ja $C$ suuruudet sekä sivun $AC$ pituus. Tarkista tulosten järkevyys vertaamalla piirrokseesi.
Vastaus
- Tällaisia kolmioita on mahdollista piirtää vain yksi.
- Kulma $B$ noin $43^\circ$, kulma $C$ noin $60^\circ$. Sivun $AC$ pituus noin 7,4 cm.
SINILAUSE JA KOSINILAUSE
Kolmion sivujen pituudet ovat 3,6 cm, 5,4 cm ja 7,8 cm.
- Piirrä kolmio. Kuinka monta erilaista ehdot täyttävää kolmiota voi piirtää?
- Kuinka suuri on kolmion suurin kulma? Entä pienin?
Vastaus
- Tällaisia kolmioita on mahdollista piirtää vain yksi.
- Suurin kulma noin $118^\circ$, pienin noin $24^\circ$.
SINILAUSE JA KOSINILAUSE
Kolmion kahden sivun pituudet ovat 8,2 cm ja 6,2 cm. Jälkimmäisen sivun vastainen kulma on 45 astetta.
- Piirrä kolmio. Kuinka monta erilaista ehdot täyttävää kolmiota voi piirtää?
- Laske kolmion muiden kulmien suuruudet ja kolmannen sivun pituus.
Vastaus
- Tällaisia kolmioita on mahdollista piirtää kaksi erilaista.
- Vaihtoehto 1: noin $69^\circ$ ja $66^\circ$ sekä noin 8,0 cm.
Vaihtoehto 2: noin $111^\circ$ ja $24^\circ$ sekä noin 3,6 cm.
SINILAUSE JA KOSINILAUSE
Kolmion sivut ovat $10$, $4\sqrt{2}$ ja $2\sqrt{17}$.
- Osoita, että kolmio on suorakulmainen.
- Minkä kahden sivun välinen kulma on suora kulma?
Vastaus
- Vinkki: teoreema 9.
- Lyhyimpien sivujen eli sivujen $4\sqrt{2}$ ja $2\sqrt{17}$ välinen kulma.
TEHTÄVÄSARJA III
- Suorakulmaisen kolmion hypotenuusan pituus on 5 ja toisen kateetin pituus 2. Laske toisen kateetin pituus.
- Laske neliön piiri, kun sen lävistäjän pituus on 6.
Vastaus
- $\sqrt{21}$
- $12\sqrt{2}$
- Kolmion kulmat muodostavat aritmeettisen jonon, ja yhden kulman suuruus on $103^\circ$. Määritä kulmien suuruudet asteina.
- Kolmion kulmat muodostavat geometrisen jonon, ja yhden kulman suuruus on $\frac{\pi}{7}$ radiaania. Määritä kulmien suuruudet radiaaneina.
Vastaus
- Kulmien suuruudet $17^\circ$, $60^\circ$ ja $103^\circ$.
- Kulmien suuruudet $\frac{(3-2\sqrt{2})\pi}{7}$, $\frac{\pi}{7}$ ja $\frac{(3+2\sqrt{2})\pi}{7}$
- Suorakulmaisen kolmion kateettien ja hypotenuusan pituudet $a < b < c$ muodostavat geometrisen jonon. Määritä jonon suhdeluku $q$.
- Suorakulmaisen kolmion kateettien ja hypotenuusan pituudet $a < b < c$ muodostavat aritmeettisen jonon. Määritä suhde $a : b : c$.
Vastaus
- $q = \sqrt{\dfrac{1 + \sqrt{5}}{2}}$
- $a:b:c = 3:4:5$
Laske oheisen kuvan suorakulmaisen kolmion $ABC$ pinta‐alan tarkka arvo.
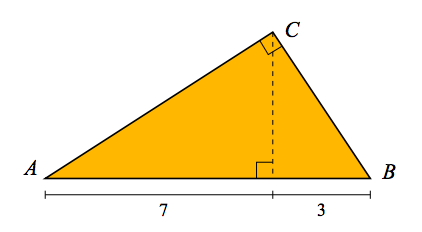
[Pitkä K2013/4]
Vastaus
$5\sqrt{21}$
Suorakulmaisessa kolmiossa $ABC$ kateetin $AB$ pituus on 4,4 cm ja hypotenuusan $AC$ pituus 8,1 cm.
- Laske kateetin $BC$ pituus.
- Laske kolmion terävien kulmien suuruudet 0,1 asteen tarkkuudella.
- Laske kolmion pinta-ala 0,1 neliösenttimetrin tarkkuudella.

[Lyhyt K2015/4]
Vastaus
- 6,8 cm
- $57{,}1^\circ$
- $15{,}0 \text{ cm}^2$
Liito-oravan vaakasuora siirtymä suoraviivaisessa liidossa on parhaimmillaan 3,3-kertainen korkeuden vähenemiseen verrattuna.
- Huippukuntoinen liito-orava aikoo liitää 60 metriä leveän aukion yli. Kuinka korkealta puusta sen täytyy ponnistaa, jotta se laskeutuisi aukion toisella puolella olevaan puuhun yhden metrin korkeudelle? Anna vastaus metrin tarkkuudella.
- Kuinka suuressa kulmassa vaakatasoon nähden a-kohdan liito-orava liitää? Anna vastaus asteen tarkkuudella.
Vastaus
- 19 m
- $17^\circ$ alaviistoon
Tasakylkisen suorakulmaisen kolmion kateetin pituus on $a$. Kolmion sisälle asetetaan kuvion mukaisesti pienempi tasakylkinen kolmio, jonka yksi kärki sijaitsee alkuperäisen kolmion hypotenuusalla. Lisäksi jana $AB$ on hypotenuusan suuntainen. Määritä pienemmän kolmion suurin mahdollinen pinta‐ala.
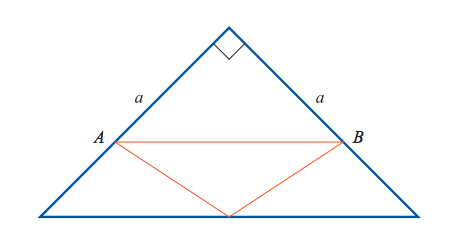
[Pitkä S2015/7]
Vastaus
$\frac{1}{8}a^2$
Tehtävänä on todistaa niin sanottu kolmion kulmanpuolittajalause: Kolmion kulman puolittaja jakaa vastakkaisen sivun osiin, joiden suhde on yhtä suuri kuin kulman viereisten sivujen suhde. Alla olevan kuvion merkinnöillä siis $$\frac{BD}{CD} = \frac{AB}{AC}$$
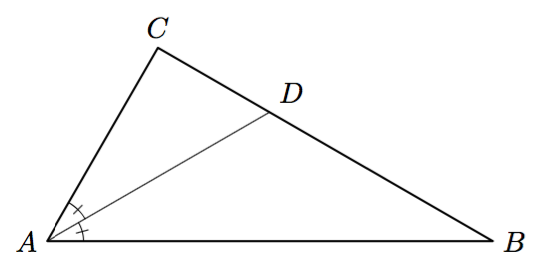
- Piirrä vihkoosi kolmio $ABC$ ja kulman $A$ puolittaja. Merkitse kulmanpuolittajan ja sivun $BC$ leikkauspistettä kirjaimella $D$ kuten yllä olevassa kuvassa.
- Piirrä kärjestä $B$ normaali (eli kohtisuora jana) kulman $A$ puolittajalle tai sen jatkeelle. Merkitse normaalin ja kulmanpuolittajan leikkauspistettä kirjaimella $P$.
- Piirrä kärjestä $C$ normaali kulman $A$ puolittajalle tai sen jatkeelle. Merkitse normaalin ja kulmanpuolittajan leikkauspistettä kirjaimella $Q$.
- Perustele, että kolmiot $BPD$ ja $CQD$ ovat yhdenmuotoiset.
- Perustele, että kolmiot $APB$ ja $AQC$ ovat yhdenmuotoiset.
- Osoita, että $$\frac{BD}{CD} = \frac{AB}{AC}$$ Vinkki: Onko kolmioilla $BPD$ ja $APB$ jokin yhteinen sivu? Entä kolmioilla $CQD$ ja $AQC$? Muodosta sopivia verrantoja.
Kolmion $ABC$ kulman $C$ puolittaja leikkaa sivun $AB$ pisteessä $D$. Pisteiden välisille etäisyyksille on voimassa $CD = 6$, $AD = 4$ ja $DB = 3$. Määritä kolmion sivujen $AC$ ja $BC$ pituuksien tarkat arvot.
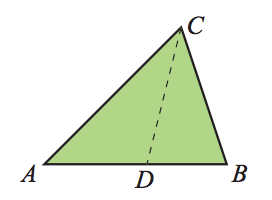
[Pitkä S2013/6]
Vastaus
$AC = 8$ ja $BC = 6$
Alla olevassa kuviossa on silityslauta sivusta katsottuna. Siihen liittyvät mitat on merkitty kuvioon. Laske silityslaudan korkeus lattiasta.
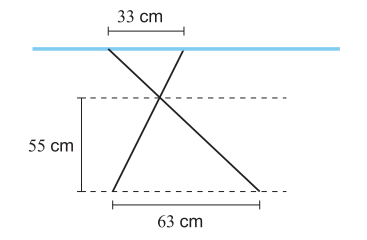
[Lyhyt S2015/5]
Vastaus
84 cm
Kuinka monta prosenttia alla olevan suorakulmion pinta-alasta on väritetty siniseksi?
Vastaus
37,5 %.
Vartiotornin korkeus on 15 metriä. Tornista 30 metrin etäisyydellä on 2,5 metriä korkea muuri. Muurin takana piileksii 185 cm pitkä henkilö. Kuinka kaukana muurista hän voi liikkua niin, ettei häntä havaita vartiotornista?
Vastaus
Enintään 1,56 metrin etäisyydellä.
Topi haluaa järjestää huoneensa uudelleen. Onko hänen mahdollista raahata 209 cm pitkä ja 106 cm leveä sänky huoneen 2,3 m pitkän päätyseinän vierestä toisen seinän viereen sänkyä kallistamatta?
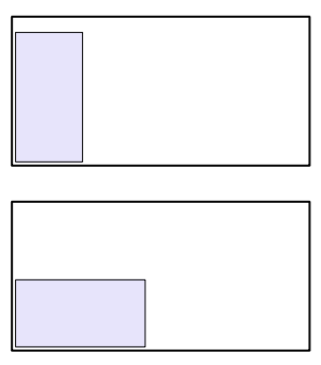
Vastaus
Sängyn lävistäjä on noin 234 cm, joten se on suurempi kuin huoneen leveys (230 cm). Sänky ei siten mahdu pyörähtämään huoneessa poikittain.
Lentokone lähestyy Oulunsalon kenttää kolmen asteen kulmassa maahan nähden. Kiitoradan pituus on 2,5 km, ja kone koskettaa kiitorataa 300 metrin päässä sen alkupäästä. Kuinka kaukana kiitoradan alkupäästä (vaakasuoraan ajateltuna) kone oli 500 jalan korkeudessa (1 jalka = 0,3048 m)? Kuinka kauan tästä kului maakosketukseen, jos lentokoneen lähestymisnopeus ilman suhteen oli 270 km/h? Oletetaan, että sää oli tyyni.
[Lyhyt K2007/7]
Vastaus
Etäisyys oli noin 2600 m ja aikaa kului noin 39 sekuntia.
Suunnistusradan ensimmäinen rasti oli lähtöpaikalta 950 metriä eteläkaakkoon (kompassisuunta 157,5 astetta). Lähdettyään ensimmäiseltä rastilta ja juostuaan 400 metriä suunnistaja tuli suoralle pohjois-etelä-suuntaiselle tielle, jonka varrella lähtöpaikka oli. Kuinka kaukana suunnistaja oli lähtöpaikalta?
Vastaus
Suunnistajan etäisyys lähtöpaikasta oli noin 710 metriä tai noin 1040 metriä.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

