Toisen asteen potenssifunktio ja neliöjuuri
Luvun tavoitteet
Tämän luvun tavoitteena on, että tunnet toisen asteen potenssifunktion ja tiedät, mitä luvun neliöjuurella tarkoitetaan. Osaat
- määrittää neliöjuurten tarkkoja arvoja neliöjuuren määritelmän perusteella tapauksissa, joissa tuloksena on luonnollinen luku tai rationaaliluku
- ratkaista muotoa $x^2 = a$ olevat neliöyhtälöt neliöjuurten avulla
- sieventää neliöjuurilausekkeita neliöjuurten laskusääntöjen avulla
Toisen asteen potenssifunktio ja neliöjuuri
Tässä kappaleessa tutustutaan niin sanottuun toisen asteen potenssifunktioon ja palautetaan mieleen, mitä luvun neliöjuuri tarkoittaa.
MÄÄRITELMÄ: TOISEN ASTEEN POTENSSIFUNKTIO
Funktiota $f(x) = x^2$ sanotaan toisen asteen potenssifunktioiksi.
Toisen asteen potenssifunktion kuvaaja on piirretty alla olevaan kuvaan. Se on muodoltaan paraabeli.
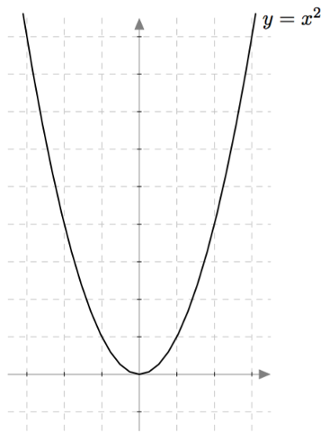
Toisen asteen potenssifunktio
Päättele yllä olevan kuvaajan avulla vastaukset seuraaviin kysymyksiin:
- Mikä on funktion $f(x) = x^2$ arvo kohdassa $x = -1$?
- Missä kohdissa funktio $f(x) = x^2$ saa arvon $4$?
- Mikä on funktion $f(x) = x^2$ pienin arvo?
- Kuinka monta ratkaisua on yhtälöllä $x^2 = 6$?
- Kuinka monta ratkaisua on yhtälöllä $x^2 = -1$?
Vastaus
- $f(-1) = 1$
- Kohdassa $x = -2$ ja kohdassa $x = 2$.
- Pienin arvo on $0$.
- Kaksi ratkaisua.
- Ei yhtään ratkaisua.
Toisen asteen potenssifunktion $f(x) = x^2$ kuvaajasta nähdään, että yhtälöllä $x^2 = 7$ on kaksi ratkaisua:
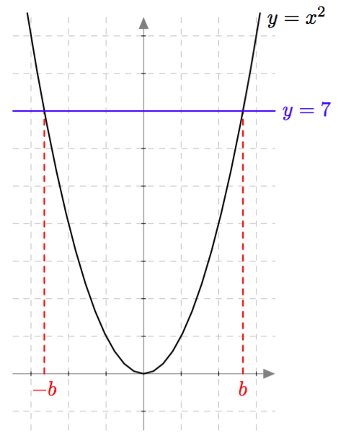
Positiivista ratkaisua, joka on merkitty kuvaan kirjaimella $b$, sanotaan luvun $7$ neliöjuureksi. Luvun $7$ neliöjuuri on siis sellainen positiivinen luku, jonka toinen potenssi on seitsemän. Vastaavasti määritellään muidenkin epänegatiivisten lukujen neliöjuuret.
Epänegatiivisia lukuja ovat luku nolla sekä kaikki positiiviset luvut. Luku $a$ on siis epänegatiivinen, jos ja vain jos $a \geq 0$. Negatiivisille luvuille neliöjuurta ei määritellä.
MÄÄRITELMÄ: NELIÖJUURI
Luvun $a \geq 0$ neliöjuuri tarkoittaa lukua $b \geq 0$, jolle pätee $$b^2 = a.$$ Luvun $a$ neliöjuurelle käytetään merkintää $\sqrt{a}.$
Jos luvun $a$ neliöjuurelle käytetään merkintää $\sqrt{a}$, pätee sille siis määritelmän mukaan kaksi asiaa: $\sqrt{a} \geq 0$ ja $\left(\sqrt{a}\right)^2 = a$.
Neliöjuuren merkintää käyttäen edellinen kuva näyttää tältä:
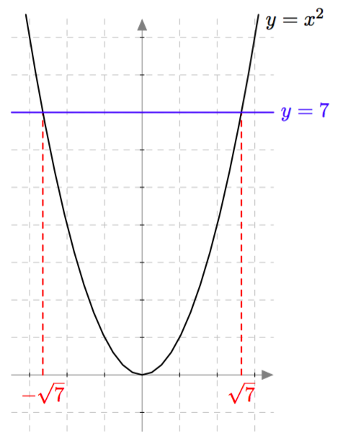
Neliöjuuri
Päättele seuraavien neliöjuurten arvo. Voit käyttää apuna yllä olevaa kuvaajaa.
- $\sqrt{4}$
- $\sqrt{1}$
- $\sqrt{0}$
- $\sqrt{9}$
Vastaus
- $\sqrt{4} = 2$
- $\sqrt{1} = 1$
- $\sqrt{0} = 0$
- $\sqrt{9} = 3$
Luvun $a$ neliöjuurelta vaaditaan neliöjuuren määritelmän mukaan kaksi asiaa: sen pitää olla epänegatiivinen ja sen toisen potenssin pitää olla yhtä suuri kuin luku $a$. Esimerkiksi luvulle $\frac{1}{2}$ pätee $\frac{1}{2} \geq 0$ ja $\left(\frac{1}{2}\right)^2 = \frac{1}{2}\cdot \frac{1}{2} = \frac{1}{4}$, joten se on luvun $\frac{1}{4}$ neliöjuuri. Voidaan siis merkitä $$\sqrt{\frac{1}{4}} = \frac{1}{2.}$$
Neliöjuuri
Määritä seuraavien neliöjuurten arvo kokeilemalla ja perustelemalla tulos sen jälkeen samaan tapaan kuin edellä.
- $\sqrt{36}$
- $\sqrt{100}$
- $\sqrt{49}$
- $\sqrt{144}$
Vastaus
- $\sqrt{36} = 6$
- $\sqrt{100} = 10$
- $\sqrt{49} = 7$
- $\sqrt{144} = 12$
Neliöjuuri
Merkinnässä $\sqrt{a}$ neliöjuuren alla olevaa lukua $a$ sanotaan juurrettavaksi. Määritä seuraavien neliöjuurten arvo kokeilemalla ja perustelemalla tulos sen jälkeen samaan tapaan kuin edellä. Kannattaa aloittaa sieventämällä juurrettava.
- $\sqrt{5^2}$
- $\sqrt{(-9)^2}$
- $\sqrt{11^2}$
- $\sqrt{\left(-\dfrac{1}{3}\right)^2}$
Vastaus
- $\sqrt{5^2} = 5$
- $\sqrt{(-9)^2} = 9$
- $\sqrt{11^2} = 11$
- $\sqrt{\left(-\dfrac{1}{3}\right)^2} = \dfrac{1}{3}$
Neliöjuuri
Tarkastele edellisen tehtävän vastauksiasi ja päättele niiden avulla, mikä ehto luvun $a$ pitää toteuttaa, jotta
- $\sqrt{a^2} = a$
- $\sqrt{a^2} = -a$
Vastaus
- $a \geq 0$
- $a < 0$
Toisen asteen potenssifunktion kuvaajan avulla voidaan ratkaista sellaisia toisen asteen yhtälöitä, jotka ovat muotoa $x^2 = a$. Esimerkiksi alla olevasta kuvasta nähdään, että yhtälöllä $x^2 = 7$ on kaksi ratkaisua: $x_1 = \sqrt{7}$ ja $x_2 = -\sqrt{7}$. Sama asia voidaan ilmaista myös sanomalla, että yhtälö $x^2 = 7$ toteutuu, jos ja vain jos $x = \sqrt{7}$ tai $x = -\sqrt{7}$.
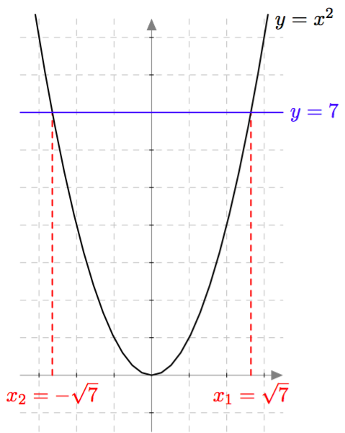
Yhtälön ratkaiseminen
Päättele yllä olevan kuvaajan avulla, kuinka monta ratkaisua seuraavilla yhtälöillä on. Jos yhtälöllä on ratkaisu tai ratkaisuja, mitä ne ovat?
- $x^2 = 0$
- $x^2 = 2$
- $x^2 = 5$
- $x^2 = -3$
Vastaus
- Yksi ratkaisu: $x = 0$
- Kaksi ratkaisua: $x = \sqrt{2}$ tai $x = -\sqrt{2}$
- Kaksi ratkaisua: $x = \sqrt{5}$ tai $x = -\sqrt{5}$
- Ei ratkaisua.
Kaikki sellaiset toisen asteen yhtälöt, joissa esiintyy vain tuntemattoman toinen potenssi, saadaan ratkaistua samaan tapaan kuin edellä. Ensin yhtälö täytyy vain muuttaa muotoon $x^2 = a$. Tarkastellaan esimerkiksi yhtälöä $$4x^2 - 3 = 0.$$ Kun sen molemmille puolille lisätään luku $3$, päädytään yhtälöön $$4x^2 = 3.$$ Tämä yhtälön molemmat puolet voidaan jakaa luvulla $4$, jolloin saadaan yhtälö $$x^2 = \frac{3}{4}.$$ Tämä yhtälö toteutuu, jos ja vain jos $$x = \sqrt{\frac{3}{4}} \quad \text{ tai } \quad x = -\sqrt{\frac{3}{4}}.$$ Ratkaisun aikana tarkasteltuja yhtälöitä ja niiden ratkaisuja on havainnollistettu alla olevassa kuvassa. Huomaa, että kaikilla yhtälöillä on samat ratkaisut kuten pitääkin.
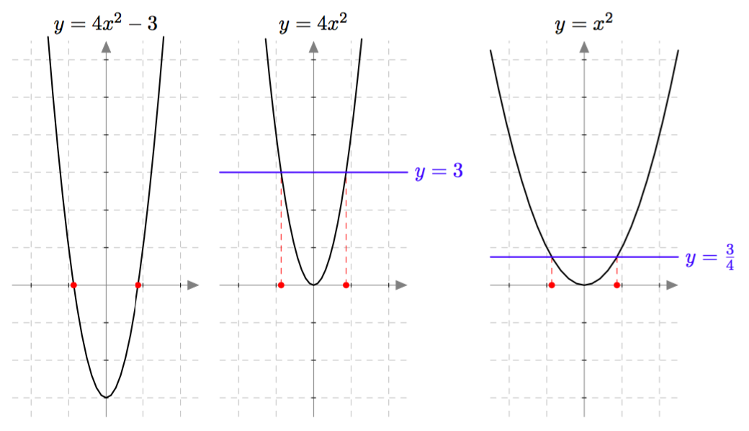
Yhtälön ratkaiseminen
Ratkaise seuraavat yhtälöt muuttamalla ne ensin muotoon $x^2 = a$ ja päättelemällä ratkaisut sen jälkeen.
- $5x^2 - 100 = 0$
- $9x^2 - 4 = 0$
- $21 - 7x^2 = 0$
- $27 + 3x^2 = 0$
Vastaus
- Kaksi ratkaisua: $x = \sqrt{20} = 2\sqrt{5}$ tai $x = -\sqrt{20} = -2\sqrt{5}$
- Kaksi ratkaisua: $x = \dfrac{2}{3}$ tai $x = -\dfrac{2}{3}$
- Kaksi ratkaisua: $x = \sqrt{3}$ tai $x = -\sqrt{3}$
- Ei ratkaisua, sillä yhtälön vasen puoli aina suurempi tai yhtä suuri kuin 27.
Neliöjuurilla laskeminen
Edellisessä kappaleessa ratkaistiin yhtälö $4x^2 - 3 = 0$. Ratkaisuiksi saatiin $$x_1 = \sqrt{\frac{3}{4}} \quad \text{ ja } \quad x_2 = -\sqrt{\frac{3}{4}}.$$ Tässä kappaleessa harjoitellaan neliöjuurilla laskemista ja opitaan muun muassa sieventämään nämä ratkaisut toiseen muotoon.
Neliöjuurten tulo ja osamäärä
- Laske laskimella, mitä on $\sqrt{2}\sqrt{8}$. Onko saamasi tulos jonkin kokonaisluvun neliöjuuri? Miten samaan tulokseen voisi päätyä käyttämällä neliöjuurta vain kerran?
- Laske laskimella, mitä on $\dfrac{\sqrt{12}}{\sqrt{3}}$. Onko saamasi tulos jonkin kokonaisluvun neliöjuuri? Miten samaan tulokseen voisi päätyä käyttämällä neliöjuurta vain kerran?
Vastaus
- $\sqrt{2}\sqrt{8} = \sqrt{2\cdot 8} = \sqrt{16} = 4$
- $\dfrac{\sqrt{12}}{\sqrt{3}} = \sqrt{\dfrac{12}{3}} = \sqrt{4} = 2$
Neliöjuuren määritelmän mukaan luku $x$ on luvun $y \geq 0$ neliöjuuri, jos se toteuttaa kaksi ehtoa:
- luvun $x$ pitää olla epänegatiivinen eli $x \geq 0$
- luvun $x$ toisen potenssin pitää olla yhtä suuri kuin $y$ eli $x^2 = y$.
Seuraavan teoreeman perustelussakin tarkistetaan nämä kaksi ehtoa, kun osoitetaan, että neliöjuurten tulo on yhtä suuri kuin tulon neliöjuuri.
TEOREEMA
Oletetaan, että $a \geq 0$ ja $b \geq 0$. Lukujen $a$ ja $b$ neliöjuurten tulo on luvun $ab$ neliöjuuri eli $$\sqrt{a}\sqrt{b} = \sqrt{ab}$$
Perustelu: Näytetään, että tulo $\sqrt{a}\sqrt{b}$ toteuttaa luvun $ab$ neliöjuurelta vaaditut ehdot.
- Neliöjuuren määritelmän mukaan $\sqrt{a} \geq 0$ ja $\sqrt{b} \geq 0$. Kahden epänegatiivisen luvun tulo on epänegatiivinen, joten $\sqrt{a}\sqrt{b} \geq 0$.
- Lasketaan tulon $\sqrt{a}\sqrt{b}$ toinen potenssi potenssin laskusääntöjen avulla: $$\left(\sqrt{a}\sqrt{b}\right)^2 = \left(\sqrt{a}\right)^2\left(\sqrt{b}\right)^2 = ab$$
Tulo $\sqrt{a}\sqrt{b}$ on siis epänegatiivinen ja sen toinen potenssi on yhtä suuri kuin $ab$. Siis $\sqrt{a}\sqrt{b} = \sqrt{ab}$.
Neliöjuurten osamäärä
Edellisessä teoreemassa osoitettiin, että $\sqrt{a}\sqrt{b} = \sqrt{ab}$. Nyt tehtävänä on perustella vastaava neliöjuurten osamäärää koskeva tulos.
- Lue edellinen teoreema ja sen perustelu huolellisesti. Mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
- Oletetaan, että $a \geq 0$ ja $b > 0$. Selitä omin sanoin, miksi osamäärä $\dfrac{\sqrt{a}}{\sqrt{b}}$ on määritelty. Mikä on pienin arvo, jonka se voi saada? Voiko kyseinen osamäärä olla negatiivinen?
- Sievennä lauseke $\left(\dfrac{\sqrt{a}}{\sqrt{b}}\right)^2$ mahdollisimman pitkälle potenssin laskusääntöjen tai potenssin määritelmän avulla. Muista myös neliöjuuren määritelmä.
- Selitä omin sanoin, miten edelliset kohdat osoittavat, että $$\dfrac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$$
Vastaus
- Osamäärä $\dfrac{\sqrt{a}}{\sqrt{b}}$ on määritelty, sillä oletuksen mukaan $b > 0$ ja siten $\sqrt{b} \neq 0$. Osamäärän pienin mahdollinen arvo on nolla. Osamäärä ei voi olla negatiivinen, sillä nimittäjä on aina positiivinen ja osoittaja on positiivinen tai nolla.
- \begin{align*} \left(\dfrac{\sqrt{a}}{\sqrt{b}}\right)^2 &= \frac{\left(\sqrt{a}\right)^2}{\left(\sqrt{b}\right)^2} \\[2mm] &= \frac{a}{b} \end{align*}
- Lauseke $$ \dfrac{\sqrt{a}}{\sqrt{b}} $$ täyttää neliöjuuren määritelmän molemmat ehdot: se on epänegatiivinen ja sen toinen potenssi on $$ \dfrac{a}{b}. $$
Seuraava teoreema perusteltiin äskeisessä tehtävässä:
TEOREEMA
Oletetaan, että $a \geq 0$ ja $b > 0$. Lukujen $a$ ja $b$ neliöjuurten osamäärä on luvun $\dfrac{a}{b}$ neliöjuuri eli $$\dfrac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$$
Neliöjuurten tulo ja osamäärä
Sievennä seuraavat lausekkeet mahdollisimman pitkälle teoreemojen 1 ja 2 avulla:
- $\sqrt{3}\sqrt{27}$
- $\sqrt{8}\sqrt{18}$
- $\dfrac{\sqrt{500}}{\sqrt{5}}$
- $\dfrac{\sqrt{6}}{\sqrt{2}}$
Vastaus
- $\sqrt{3}\sqrt{27} = \sqrt{81} = 9$
- $\sqrt{8}\sqrt{18} = \sqrt{144} = 12$
- $\dfrac{\sqrt{500}}{\sqrt{5}} = \sqrt{100} = 10$
- $\dfrac{\sqrt{6}}{\sqrt{2}} = \sqrt{3}$
Kokonaislukujen neliöjuuret sievennetään yleensä muotoon, jossa juurrettavana on mahdollisimman pieni kokonaisluku. Sieventäminen onnistuu teoreeman 1 avulla, jos juurrettavalla on tekijänä jonkin kokonaisluvun neliö. Esimerkiksi \begin{align*} \sqrt{72} &= \sqrt{2 \cdot 36} \\ &= \sqrt{2}\cdot \sqrt{36} \\ &= \sqrt{2}\cdot 6 \\ &= 6\sqrt{2} \end{align*}
Neliöjuurten sieventäminen
Sievennä seuraavat neliöjuuret teoreemaa 1 hyödyntäen samaan tapaan kuin edellä. Aloita kirjoittamalla juurrettava sopivana tulona.
- $\sqrt{8}$
- $\sqrt{12}$
- $\sqrt{90}$
- $\sqrt{75}$
Vastaus
- $\sqrt{8} = \sqrt{4\cdot 2} = 2\sqrt{2}$
- $\sqrt{12} = \sqrt{4\cdot 3} = 2\sqrt{3}$
- $\sqrt{90} = \sqrt{9\cdot 10} = 3\sqrt{10}$
- $\sqrt{75} = \sqrt{25\cdot 3} = 5\sqrt{3}$
Neliöjuurten sieventäminen helpottaa niiden yhteen- ja vähennyslaskua. Esimerkiksi lauseke $\sqrt{12} - \sqrt{27}$ saadaan sieventämällä huomattavasti yksinkertaisempaan muotoon: \begin{align*} \sqrt{12} - \sqrt{27} &= \sqrt{4\cdot 3} - \sqrt{9 \cdot 3} \\ &= \sqrt{4}\sqrt{3} - \sqrt{9}\sqrt{3} \\ &= 2\sqrt{3} - 3\sqrt{3} \\ &= (2-3)\sqrt{3}\\ &= - \sqrt{3} \end{align*}
Neliöjuurten sieventäminen
- Laske laskimella, mitä on $\sqrt{20} + \sqrt{45}$. Onko saamasi tulos jonkin kokonaisluvun neliöjuuri? Onko neliöjuurten summalla samanlainen ominaisuus kuin teoreemassa 1 todistettiin neliöjuurten tulolle?
- Sievennä neliöjuuret $\sqrt{20}$ ja $\sqrt{45}$ mahdollisimman pitkälle teoreeman 1 tulosta käyttäen samaan tapaan kuin edellisessä tehtävässä.
- Laske summa $\sqrt{20} + \sqrt{45}$.
Vastaus
- Kokeilemalla on mahdollista huomata, että $\sqrt{20} + \sqrt{45}$ näyttäisi olevan sama kuin $\sqrt{125}$. Vastaava ominaisuus kuin teoreemassa 1 ei päde tässä tapauksessa, sillä $\sqrt{20} + \sqrt{45} \neq \sqrt{65}$.
- $\sqrt{20} = \sqrt{4\cdot 5} = 2\sqrt{5}$ ja $\sqrt{45} = \sqrt{9 \cdot 5} = 3\sqrt{5}$
- \begin{align*} \sqrt{20} + \sqrt{45} &= 2\sqrt{5} + 3\sqrt{5} \\ &= 5\sqrt{5} \\ (&= \sqrt{25 \cdot 5} = \sqrt{125}\,) \end{align*}
TEHTÄVÄSARJA II
Neliöjuuri
Päättele seuraavien neliöjuurten arvo käyttämättä laskimen neliöjuurinappulaa.
- $\sqrt{81}$
- $\sqrt{121}$
- $\sqrt{64}$
- $\sqrt{144}$
Voit tarkistaa tulokset laskimella.
Neliöjuuri
Palauta mieleesi neliöjuuren määritelmä ja päättele seuraavien neliöjuurien tarkat arvot:
- $\sqrt{7^2}$
- $\sqrt{(-5)^2}$
- $\sqrt{(\sqrt{3}-1)^2}$
- $\sqrt{(\sqrt{3}-2)^2}$
Vihje c- ja d-kohtiin: päättele ensin, onko juurrettavassa ensiintyvän potenssin kantaluku positiivinen vai negatiivinen.
Vastaus
- $7$
- $5$
- $\sqrt{3}-1$
- $2-\sqrt{3}$ eli $-(\sqrt{3}-2)$
Yhtälön ratkaiseminen
Ratkaise seuraavat yhtälöt. Jos yhtälöllä ei ole yhtään ratkaisua, selitä omin sanoin, miksi näin on.
- $2x^2-2 = 0$
- $x^2+5 = 0$
- $8-x^2 = 0$
- $-4x^2 = 0$
Vastaus
- $x = 1\ $ tai $\ x = -1$
- Yhtälöllä ei ole ratkaisua, sillä toinen potenssi ei koskaan ole negatiivinen. Mikään luku ei siis toteuta yhtälöä $x^2 = -5$.
- $x = \sqrt{8}\ $ tai $\ x = -\sqrt{8}$
- $x = 0$
Neliöjuurilla laskeminen
Sievennä seuraavat neliöjuurilausekkeet neliöjuurten laskusääntöjen eli teoreemojen 1 ja 2 avulla:
- $\sqrt{3}\sqrt{12}$
- $\sqrt{1600}$
- $\dfrac{\sqrt{60}}{\sqrt{15}}$
- $\sqrt{\dfrac{16}{81}}$
Vastaus
- $6$
- $40$
- $2$
- $\dfrac{4}{9}$
Neliöjuurilla laskeminen
Muuta juurrettavat sekaluvut murtolukumuotoon ja sievennä neliöjuurten laskusääntöjen avulla:
- $\sqrt{2\frac{1}{4}}$
- $\sqrt{1\frac{9}{16}}$
- $\sqrt{5\frac{4}{9}}$
Vastaus
- $\dfrac{3}{2}$
- $\dfrac{5}{4}$
- $\dfrac{7}{3}$
Yhtälön ratkaiseminen
- Selvitä itsellesi, miten neliön pinta-ala lasketaan, jos neliön sivun pituus on $a$. Voit kysyä vaikka kaverilta tai katsoa netistä.
- Neliön pinta-ala on $169 \text{ cm}^2$. Mikä on sen sivun pituus?
Vastaus
- Sivun pituus on 13 cm.
Yhtälön ratkaiseminen
Neliön muotoisen huoneen lattia päällystettiin 15 cm leveällä laudalla, jota kului 153,6 m. Mitkä olivat lattian mitat? Anna vastaus kahden merkitsevän numeron tarkkuudella.
Vastaus
Huoneen jokainen seinä oli noin 4,8 metriä leveä.
Yhtälön ratkaiseminen
Pythagoraan lauseen mukaan suorakulmaisen kolmion pisimmän sivun eli hypotenuusan neliö on lyhyempien sivujen eli kateettien neliöiden summa. Alla olevan kuvan merkinnöillä $$c^2 = a^2 + b^2.$$
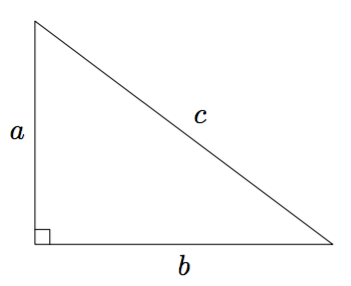
Laske suorakulmaisen kolmion kolmas sivu, jos
- kateettien pituudet ovat 12 ja 5
- hypotenuusan pituus on 16 ja toisen kateetin pituus on 15.
Vastaus
- $13$
- $\sqrt{31}$
Neliöjuurten sieventäminen
Sievennä seuraavat neliöjuurilausekkeet teoreeman 1 avulla:
- $\sqrt{18}$
- $\sqrt{\dfrac{3}{16}}$
- $\sqrt{5}\sqrt{15}$
Vastaus
- $3\sqrt{2}$
- $\dfrac{\sqrt{3}}{4}$
- $5\sqrt{3}$
Neliöjuurten sieventäminen
Sievennä seuraavat neliöjuurilausekkeet samaan tapaan kuin tehtävässä 2.12:
- $\sqrt{2} + \sqrt{8}$
- $\sqrt{8} - \sqrt{16} + \sqrt{18} + \sqrt{36}- \sqrt{98}$
- $\dfrac{2 + \sqrt{12}}{2}$
Vastaus
- $3\sqrt{2}$
- $2-2\sqrt{2}$
- $1 + \sqrt{3}$
Neliöjuurten sieventäminen
Lavenna lausekkeet nimittäjässä esiintyvällä neliöjuurella ja supista sen jälkeen, jos mahdollista:
- $\dfrac{2}{\sqrt{5}}$
- $\dfrac{2}{\sqrt{2}}$
- $\dfrac{15}{\sqrt{5}}$
- $\dfrac{\sqrt{6}}{2\sqrt{3}}$
Vastaus
- $\dfrac{2}{5}\sqrt{5}$
- $\sqrt{2}$
- $3\sqrt{5}$
- $\dfrac{1}{2}\sqrt{2}$
TEHTÄVÄSARJA III
Pankkiin talletettiin vuoden alussa $10\,000$ euroa kahdeksi vuodeksi. Vuotuinen korkoprosentti oli koko ajan sama ja kertynyt korko liitettiin pääomaan aina vuoden lopussa.
- Kuinka suureksi pääoma kasvoi kahden vuoden aikana, jos vuotuinen korkoprosentti oli 2,1? Mikä oli vuosittaista kasvua vastaava kerroin $q$?
- Mikä oli vuotuinen korkokanta, jos pääoma kasvoi kahden vuoden aikana $10\,920{,}25$ euroksi?
Vastaus
- 10 424,41 €, $q = 1{,}021$
- $4{,}5 \ \%$
Kuinka monta prosenttia neliön sivua on pidennettävä, jotta neliön pinta-ala kasvaisi 50 prosenttia?
Vihje: merkitse alkuperäisen neliön sivun pituutta jollakin kirjaimella.
Vastaus
Noin $22{,}5 \ \%$.
- Palauta mieleesi tai tarkista esimerkiksi netistä, miten ympyrän pinta-ala lasketaan, jos sen säde tunnetaan.
- Neliöllä ja ympyrällä on sama pinta-ala. Kuinka monta prosenttia ympyrän säde on neliön sivusta?
Vastaus
- Noin 56,4 %.
Jos heilurin heilahduskulma on pieni, yhden edestakaisen heilahduksen heilauhdusajalle $T$ on voimassa likiarvokaava $$T = 2\pi\sqrt{\dfrac{L}{g}},$$ missä $L$ on heilurin varren pituus ja $g$ on painovoiman aiheuttama putoamiskiihtyvyys.
Sadan (edestakaisen) heilahduksen kokonaisajaksi mitattiin 160 s ja heilurin varren pituudeksi $0{,}637$ m. Kuinka suuri putoamiskiihtyvyys $g$ mittauspaikalla mittausten perusteella on?
Vastaus
Noin $9{,}82 \,\dfrac{\text{m}}{\text{s}^2}$
Osoita, että lukujen $\sqrt{3}$ ja $\dfrac{\sqrt{3}}{\sqrt{3}-1}$ summa ja tulo ovat yhtä suuret.
Vastaus
Sekä summaksi että tuloksi saadaan $\dfrac{3}{\sqrt{3}-1}$.
Ratkaise yhtälö $\sqrt{6}(x-\sqrt{2}) = \sqrt{3}$. Ilmoita vastaus muodossa, jossa nimittäjässä ei ole juuria.
Vastaus
$x = \dfrac{3\sqrt{2}}{2}$
Millä muuttujan $x$ arvoilla seuraavat lausekkeet on määritelty?
- $\sqrt{5x+1}$
- $\dfrac{1}{\sqrt{x-4}}$
- $\sqrt{2x-1} + \sqrt{3-x}$
Vastaus
- $x \geq -\frac{1}{5}$
- $x > 4$
- $\frac{1}{2} \leq x \leq 3$
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

