Vektorit ja $xy$-koordinaatisto
Luvun tavoitteet
Tämän luvun tavoitteena on, että tiedät, millaisia $xy$-koordinaatiston vektorit ovat. Osaat
- ilmaista $xy$-koordinaatistoon piirretyn vektorin vektoreiden $\vi$ ja $\vj$ avulla
- määrittää $xy$-koordinaatiston pisteen paikkavektorin
- määrittää vektoreiden summan ja erotuksen piirtämällä
- laskea vektoreiden summan, erotuksen ja pistetulon
- kertoa vektorin reaaliluvulla ja tiedät, miten se vaikuttaa vektorin pituuteen ja suuntaan
- määrittää kahden pisteen välisen vektorin
- laskea vektorin pituuden
- määrittää vektoreiden välisen kulman pistetulon avulla.
Vektorit
Koordinaatisto
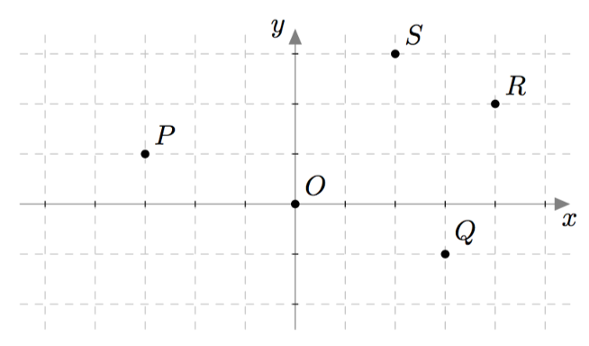
Tutki alla olevaa kuvaa. Kuinka monta yhden ruudun mittaista askelta pitää siirtyä
- $x$-akselin suunnassa, jotta päästään origosta $O$ pisteeseen $S$?
- $y$-akselin suunnassa, jotta päästään origosta $O$ pisteeseen $S$?
- $x$-akselin suunnassa, jotta päästään origosta $O$ pisteeseen $Q$?
- $y$-akselin suunnassa, jotta päästään origosta $O$ pisteeseen $Q$?
Miten voisit merkitä sitä, että pisteen $Q$ tapauksessa siirrytään $y$-akselin suunnassa alaspäin eikä ylöspäin?
VASTAUS
- kaksi askelta oikealle
- kolme askelta ylöspäin
- kolme askelta oikealle
- yksi askel alaspäin.
Tason piste ilmoitetaan lukuparina $(x,y)$. Ensimmäinen luku $x$ kertoo, missä piste sijaitsee $x$-akselin suunnassa origoon verrattuna. Toinen luku $y$ kertoo vastaavasti, missä piste sijaitsee $y$-akselin suunnassa origoon verrattuna. Näitä lukuja kutsutaan pisteen koordinaateiksi.
Esimerkiksi alla olevan kuvan pisteeseen $R$ päästään siirtymällä origosta neljä yksikköä $x$-akselin positiiviseen suuntaan ja kaksi yksikköä $y$-akselin positiiviseen suuntaan. Pistettä $R$ merkitään siis $R=(4,2)$. Pistettä $P$ merkitään puolestaan $P=(-3,1)$.

Pisteitä koordinaatistossa
- Piirrä koordinaatisto ja merkitse siihen pisteet $(1,2)$, $(1,-4)$ ja $(1,3)$.
- Merkitse koordinaatistoon kolme uutta pistettä, jotka ovat muotoa $(1,y)$, missä $y$ on kokonaisluku.
- Merkitse koordinaatistoon kaikki sellaiset pisteet, jotka ovat muotoa $(1,y)$. Millainen kuvio syntyy?
Koordinaattiakselit jakavat tason neljään osaan. Osat nimetään yleensä järjestysnumeroilla I, II, III ja IV kuten alla olevassa kuvassa. Koordinaattiakselien leikkauspistettä kutsutaan origoksi ja merkitään yleensä kirjaimella $O$.
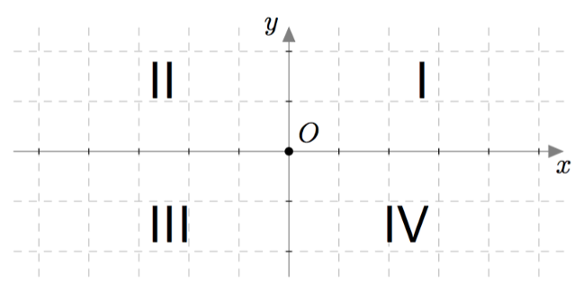
Koordinaattien etumerkit koordinaatiston eri neljänneksissä
Valitse koordinaatiston jokaiselta neljännekseltä jokin piste ja ilmoita sen koordinaatit. Miten eri neljännekset vaikuttavat pisteiden $x$- ja $y$-koordinaattien etumerkkeihin?
Alla olevassa kuvassa näkyvät vektorit $\bar{\imath}$ ja $\bar{\jmath}$. Ne ovat koordinaattiakselien suuntaisia ja yhden yksikön pituisia.
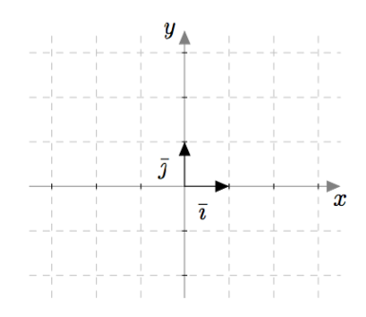
Muut vektorit voidaan esittää vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla. Esimerkiksi alla olevassa kuvassa vektori $\bar{u}$ on esitetty vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla.
Kuvasta nähdään, että vektorin $\bar{u}$ alkupisteestä päästään sen loppupisteeseen siirtymällä kaksi yksikköä $x$-akselin negatiiviseen suuntaan ja neljä yksikköä $y$-akselin positiiviseen suuntaan. Vektori $\bar{u}$ voidaan siis ilmoittaa vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla muodossa $\bar{u} = -2\bar{\imath} + 4\bar{\jmath}$.
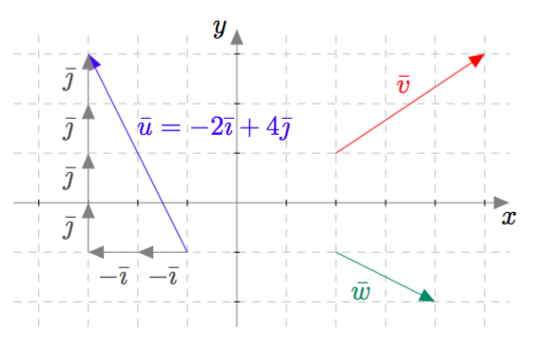
Vektoreiden esittäminen vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla
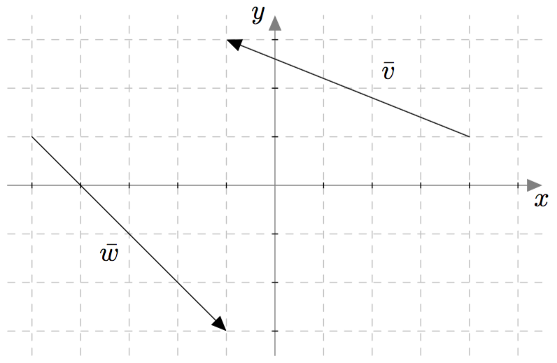
Ilmoita yllä olevassa kuvassa näkyvät vektorit $\bar{v}$ ja $\bar{w}$ vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla.
VASTAUS
$\vv = 3\vi + 2\vj$, $\vw = 2\vi - \vj$
Koordinaatistossa olevia nuolia kutsutaan siis vektoreiksi. Vektorit $\bar{\imath}$ ja $\bar{\jmath}$ ovat erityisiä, sillä ne ovat koordinaattiakselien suuntaisia ja yhden yksikön pituisia. Niiden avulla voidaan ilmaista kaikki $xy$-koordinaatiston vektorit.
Vektoreiden esittäminen vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla
- Ilmoita kaikki kuvassa näkyvät vektorit vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla.
- Selitä omin sanoin, mitä huomaat.
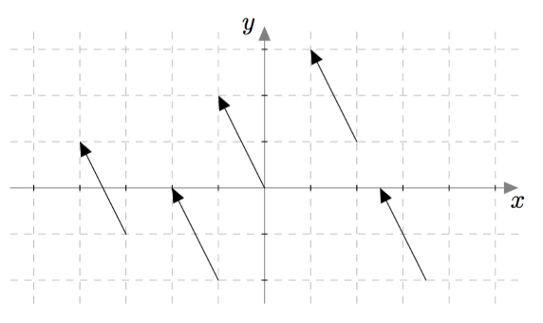
MÄÄRITELMÄ: VEKTOREIDEN SAMUUS
Kaksi vektoria ovat samat, jos ja vain jos ne voidaan esittää samalla tavalla vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla. Tarkemmin sanottuna vektorit $\vv = x_1\vi + y_1\vj$ ja $\vw = x_2\vi + y_2\vj$ ovat samat eli $\vv = \vw$, jos ja vain jos $x_1 = x_2$ ja $y_1 = y_2$.
Kuten edellisessä tehtävässä huomataan, vektoreiden samuus tarkoittaa siis sitä, että ne ovat saman pituisia ja osoittavat samaan suuntaan — niiden paikalla koordinaatistossa ei ole merkitystä.
Vektoreiden esittäminen vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla
- Ilmoita kaikki kuvassa näkyvät vektorit vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla.
- Vertaa a-kohdan tuloksia vektoreiden loppupisteiden koordinaatteihin. Kerro havaintosi omin sanoin.
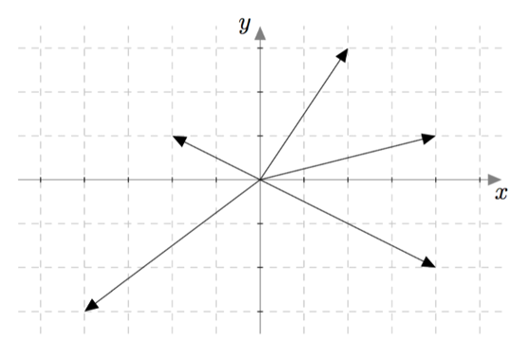
MÄÄRITELMÄ: PAIKKAVEKTORI
Vektori, joka lähtee origosta ja joka loppuu pisteeseen $P$, on pisteen $P$ paikkavektori. Pisteen $P$ paikkavektoria voidaan merkitä $\pv{OP}$.
Esimerkiksi alla olevassa kuvassa oleva vektori $\bar{v}=4\bar{\imath} + 3\bar{\jmath}$ on siis pisteen $(4,3)$ paikkavektori.
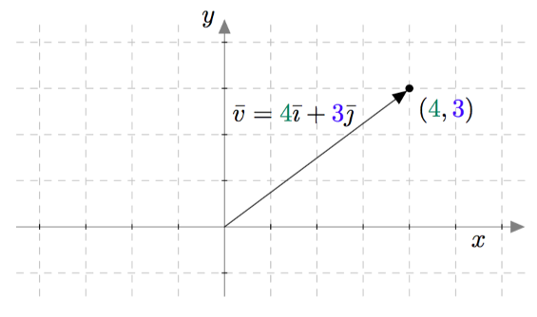
Paikkavektori
- Ilmoita alla olevan kuvan vektori $\bar{w}$ vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla. Minkä pisteen paikkavektori se on?
- Ilmoita vektori $\bar{u}$ vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla. Minkä pisteen paikkavektori se on?
- Minkä pisteiden paikkavektoreita vektorit $\bar{\imath}$ ja $\bar{\jmath}$ ovat?
- Mikä on origon paikkavektori?
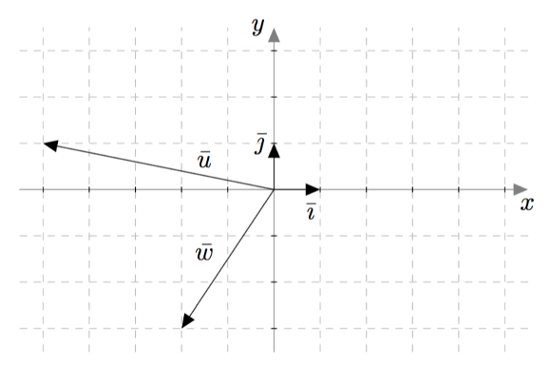
VASTAUS
- $\vw = -2\vi-3\vj$ on pisteen $(-2,-3)$ paikkavektori.
- $\vu = -5\vi+\vj$ on pisteen $(-5,1)$ paikkavektori
- Pisteiden $(1,0)$ ja $(0,1)$.
- $0\vi + 0\vj$
Paikkavektori
- Ilmaise pisteiden $A = (9,-7)$ ja $B = (-3,8)$ paikkavektorit $\pv{OA}$ ja $\pv{OB}$ vektoreiden $\vi$ ja $\vj$ avulla.
- Tiedetään, että $\pv{OP} = -4\vi-6\vj$ ja $\pv{OS} = 23\vi-78\vj$. Päättele, mitkä ovat pisteiden $P$ ja $S$ koordinaatit.
VASTAUS
- $\pv{OA} = 9\vi - 7\vj$, $\pv{OB} = -3\vi + 8\vj$
- $P = (-4,-6)$ ja $S = (23,-78)$
MÄÄRITELMÄ: NOLLAVEKTORI
Vektoria $0\bar{\imath} + 0\bar{\jmath}$ sanotaan nollavektoriksi ja merkitään $\bar{0}$.
Nollavektori $\bar{0}$ on siis vektori, jonka alkupiste ja loppupiste ovat samat. Nollavektori on origon eli pisteen $(0,0)$ paikkavektori.
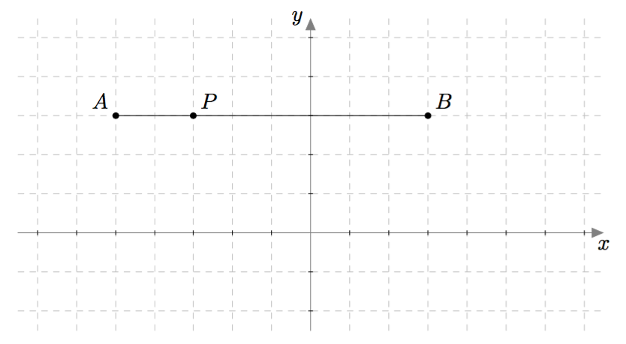
Tarkastellaan vielä alla olevaa kuvaa. Siinä piste $P$ jakaa janan $AB$ suhteessa $1:3$. Tämä nähdään siitä, että janan $AP$ pituus on 2 ja janan $PB$ pituus on 6. Näiden pituuksien suhde on $$\frac{2}{6} = \frac{1}{3}.$$ Koko jana $AB$ muodostuu siis neljästä yhtä pitkästä osasta. Jana $AP$ on yhden osan pituinen ja jana $PB$ on kolmen osan pituinen.
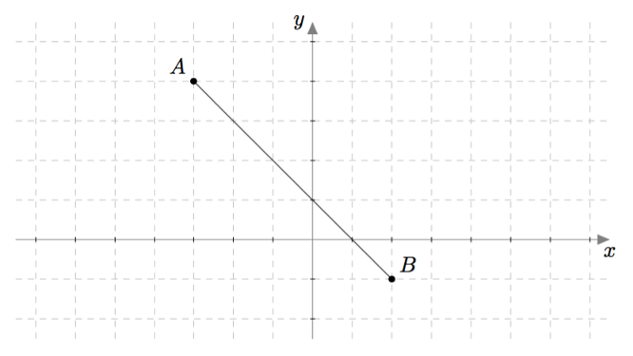
Paikkavektori
Päättele alla olevan kuvan avulla pisteen $P$ paikkavektori, jos tiedetään, että piste $P$ jakaa janan $AB$
- suhteessa 4:1
- suhteessa 2:3.
VASTAUS
- $P = (1,0)$
- $P = (-1,2)$
Vektoreiden summa
Edellä opittiin ilmaisemaan $xy$-koordinaatiston vektoreita vektoreiden $\bar{\imath}$ ja $\bar{\jmath}$ avulla. Esimerkiksi alla olevan kuvan vektori $\bar{v}$ on vektoreiden $2\bar{\imath}$ ja $4\bar{\jmath}$ summa eli $\bar{v} = 2\bar{\imath} + 4\bar{\jmath}$.
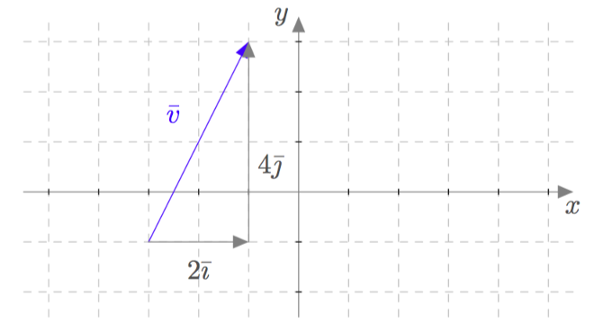
Yhteenlaskettavia $2\bar{\imath}$ ja $4\bar{\jmath}$ sanotaan vektorin $\bar{v}$ komponenteiksi. Esimerkiksi vektorin $\bar{u}=-7\bar{\imath}-3\bar{\jmath}$ komponentit ovat vektorit $-7\bar{\imath}$ ja $-3\bar{\jmath}$. Myöhemmin opitaan jakamaan $xy$-tason vektoreita myös muihin kuin koordinaattiakselien suuntaisiin komponentteihin.
Seuraavaksi sovitaan, miten lasketaan minkä tahansa vektoreiden summa. Se tehdään laskemalla vektorit komponenteittain yhteen.
MÄÄRITELMÄ: SUMMA
Vektoreiden $\bar{v}$ ja $\bar{w}$ summa $\bar{v} + \bar{w}$ saadaan laskemalla vektorit komponenteittain yhteen.
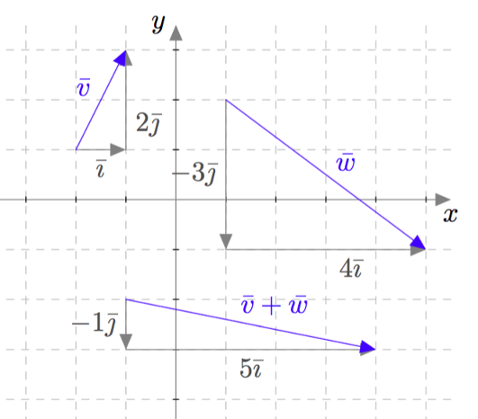
Esimerkiksi alla olevan kuvan vektoreiden $\bar{v}=\bar{\imath}+\textcolor{blue}{2}\bar{\jmath}$ ja $\bar{w} = \textcolor{darkgreen}{4}\bar{\imath}\textcolor{blue}{-3}\bar{\jmath}$ summa saadaan laskemalla yhteen $x$-akselin suuntaiset komponentit: $$ \bar{\imath} + \textcolor{darkgreen}{4}\bar{\imath} = \textcolor{darkgreen}{5}\bar{\imath} $$ sekä $y$-akselin suuntaiset komponentit: $$ \textcolor{blue}{2}\bar{\jmath}+(\textcolor{blue}{-3}\bar{\jmath})=\textcolor{blue}{2}\bar{\jmath}\textcolor{blue}{-3}\bar{\jmath}=\textcolor{blue}{-}\bar{\jmath}. $$ Vektoreiden $\bar{v}$ ja $\bar{w}$ summaksi saadaan siis \begin{align*} \bar{v} + \bar{w} &=(\bar{\imath}+\textcolor{blue}{2}\bar{\jmath}) + (\textcolor{darkgreen}{4}\bar{\imath}\textcolor{blue}{-3}\bar{\jmath}) \\ &= (\textcolor{darkgreen}{1+4})\bar{\imath} + (\textcolor{blue}{2+(-3)})\bar{\jmath} \\ &= \textcolor{darkgreen}{5}\bar{\imath} \textcolor{blue}{-} \bar{\jmath}. \end{align*}
Vektoreiden summa
Tutki vektoreita $\bar{v}=-3\bar{\imath}-4\bar{\jmath}$, $\bar{w}=9\bar{\imath}-5\bar{\jmath}$ ja $\bar{u}=-2\bar{\imath}+7\bar{\jmath}$. Laske seuraavat summat:
- $\bar{v}+\bar{w}$
- $\bar{w}+\bar{u}$
- $\bar{v}+\bar{u}$.
VASTAUS
- $6\vi - 9\vj$
- $7\vi + 2\vj$
- $-5\vi + 3\vj$
Vektoreiden summa
Tutki vektoreita $\bar{v}=2\bar{\imath}+2\bar{\jmath}$ ja $\bar{w}=\bar{\imath}+3\bar{\jmath}$.
- Piirrä vektori $\bar{v}$ koordinaatistoon.
- Piirrä vektori $\bar{w}$ koordinaatistoon siten, että se alkaa vektorin $\bar{v}$ loppupisteestä.
- Laske summa $\bar{v}+\bar{w}$.
- Piirrä summavektori $\bar{v}+\bar{w}$ koordinaatistoon siten, että se alkaa vektorin $\bar{v}$ alkupisteestä.
- Kerro omin sanoin, mitä havaitset edellisistä kohdista.
Tarkastellaan alla olevaa kuvaa. Siinä vektorit $\bar{a}=3\bar{\imath}+5\bar{\jmath}$ ja $\bar{b}=4\bar{\imath}-2\bar{\jmath}$ on piirretty peräkkäin niin, että vektori $\bar{b}$ alkaa vektorin $\bar{a}$ loppupisteestä. Vektoreiden $\bar{a}$ ja $\bar{b}$ summa on komponenteittain laskettuna \begin{align*} \bar{a}+\bar{b} &= (\textcolor{darkgreen}{3}\bar{\imath}+\textcolor{blue}{5}\bar{\jmath})+(\textcolor{darkgreen}{4}\bar{\imath}\textcolor{blue}{-2}\bar{\jmath}) \\ &= (\textcolor{darkgreen}{3+4})\bar{\imath}+(\textcolor{blue}{5+(-2)})\bar{\jmath} \\ &= \textcolor{darkgreen}{7}\bar{\imath}+\textcolor{blue}{3}\bar{\jmath}. \end{align*} Saatu summavektori alkaa vektorin $\bar{a}$ alkupisteestä ja päättyy vektorin $\bar{b}$ loppupisteeseen. Tämä ilmiö on seuraus yhteenlaskun suorittamisesta komponenteittain.
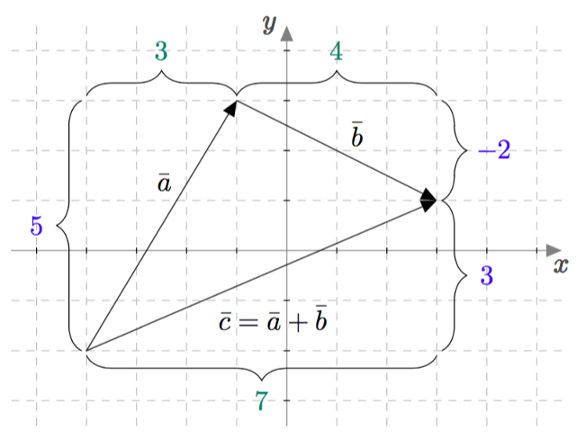
Summavektorin $\bar{a}+\bar{b}$ voi määrittää piirtämällä samaan tapaan kuin yllä olevassa kuvassa: piirretään vektori $\bar{a}$ ja piirretään sen perään vektori $\bar{b}$ niin, että se alkaa vektorin $\bar{a}$ loppupisteestä. Summavektori $\bar{a}+\bar{b}$ on vektori, joka alkaa vektorin $\bar{a}$ alkupisteestä ja päättyy vektorin $\bar{b}$ loppupisteeseen.
Vektoreiden summan määrittäminen piirtämällä
Tutki vektoreita $\bar{v}=-2\bar{\imath}+\bar{\jmath}$ ja $\bar{w}=4\bar{\imath}+4\bar{\jmath}$.
- Piirrä summavektori $\vv+\vw$ koordinaatistoon vektoreiden $\vv$ ja $\vw$ avulla.
- Päättele piirroksestasi, miten summa $\vv+\vw$ voidaan ilmaista vektoreiden $\vi$ ja $\vj$ avulla.
- Tarkista b-kohdassa saamasi tulos laskemalla yhteen vektorit $\vv$ ja $\vw$ komponenteittain.
Vektoreiden summan määrittäminen piirtämällä
Tutki vektoreita $\vu=\bar{\imath}+2\bar{\jmath}$, $\vv=-3\bar{\imath}+\bar{\jmath}$ ja $\vw=3\bar{\imath}-5\bar{\jmath}$. Piirrä seuraavat summavektorit koordinaatistoon vektoreiden $\vu, \vv$ ja $\vw$ avulla:
- $\vw+\vu+\vv$
- $\vv+\vw+\vu$
- $\vu+\vv+\vw$.
Edellisen tehtävän tulos on yksi osoitus siitä, että vektoreiden yhteenlaskun järjestyksellä ei ole merkitystä lopputuloksen kannalta. Vektoreiden yhteenlasku on siis vaihdannainen operaatio. Tämä näkyy myös alla olevassa kuvassa: vektori $4\vj+2\vi$ on sama kuin vektori $2\vi+4\vj$.
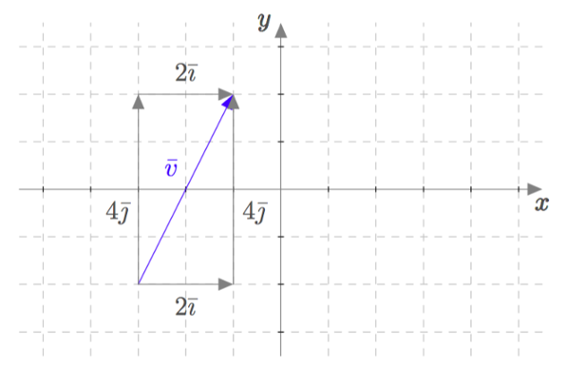
Vektorin kertominen reaaliluvulla
Tarkastellaan alla olevaa kuvaa. Vektori $\va$ voidaan ilmaista vektorin $\vj$ avulla muodossa $5\vj$. Vektori $\va$ saadaan siis kertomalla vektoria $\vj$ luvulla $5$. Sanotaan, että vektori $\va$ on vektorin $\vj$ skalaarimonikerta.
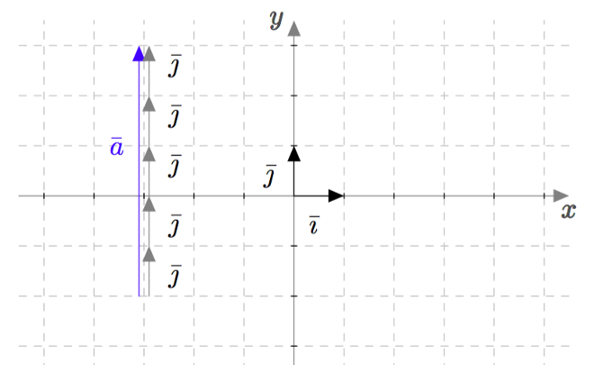
MÄÄRITELMÄ: VEKTORIN KERTOMINEN REAALILUVULLA
Vektorin $\vv$ skalaarimonikerta $r\vv$ saadaan kertomalla vektorin $\vv$ komponentit reaaliluvulla $r$.
Tarkastellaan alla olevaa kuvaa. Kerrotaan vektori $\vv=-4\vi+3\vj$ luvulla $2$. Se tehdään kertomalla vektorin molemmat komponentit kahdella. Koska $2\cdot (-4\vi)=-8\vi$ ja $2\cdot 3\vj=6\vj$, niin tulokseksi saadaan $2\vv=-8\vi + 6 \vj$.
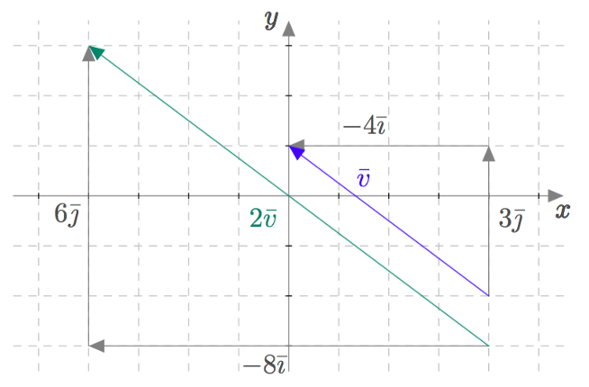
Vektorin kertominen reaaliluvulla
Tutki vektoria $\va=-\vi+2\vj$.
- Ilmoita vektorit $2\va$, $3\va$ ja $-1\va$ vektoreiden $\vi$ ja $\vj$ avulla.
- Piirrä vektorit $2\va$, $3\va$ ja $-1\va$ koordinaatistoon.
- Selitä omin sanoin, miten reaaliluvulla kertominen vaikuttaa vektoriin.
VASTAUS
- $2\va = -2\vi+4\vj$, $\quad3\va = -3\vi+6\vj\quad$ ja $\quad-1\va = \vi-2\vj$
Vektorin kertominen reaaliluvulla
- Piirrä koordinaatistoon vektorit $\va=\vi+2\vj$ ja $\vb=2\vi+4\vj$.
- Miten voisit ilmaista vektorin $\vb$ vektorin $\va$ avulla?
VASTAUS
- $\vb = 2\va$
MÄÄRITELMÄ: VASTAVEKTORI
Vektori $-1\vv$ on vektorin $\vv$ vastavektori. Sitä merkitään $-\vv$.
Alla on näkyvissä eräs vektori $\vv$ ja sen vastavektori $-\vv$.
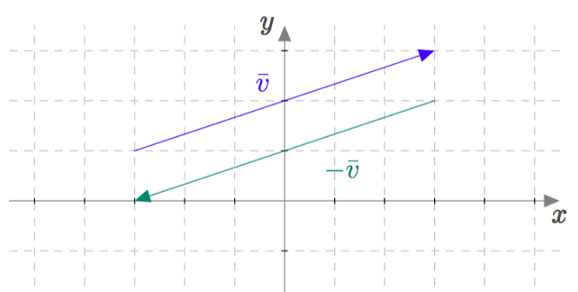
Vektorin vastavektori
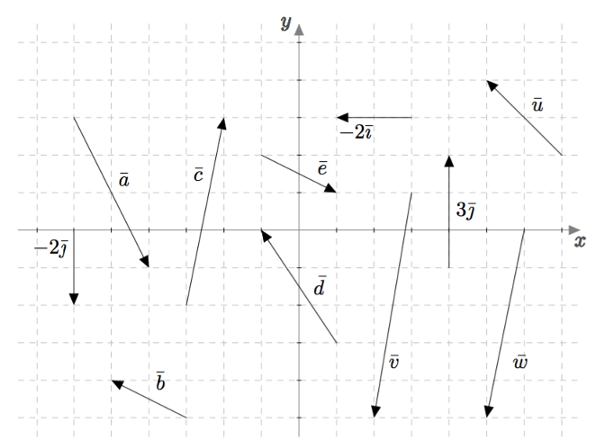
Tarkastele alla olevaa kuvaa.
- Ilmaise kaikki kuvassa näkyvät vektorit vektoreiden $\vi$ ja $\vj$ avulla.
- Mitkä näistä vektoreista ovat toistensa vastavektoreita?
VASTAUS
- $\va = 2\vi - 4\vj$, $\quad\vb = -2\vi + \vj$, $\quad\vc = \vi+ 5\vj$, $\quad\bar{d} = -2\vi + 3\vj$, $\quad\bar{e} = 2\vi - \vj$, $\quad\vv = -\vi - 6\vj$, $\quad\vw = -\vi - 5\vj$, $\quad\vu = -2\vi +2\vj$
- $\vb = -\bar{e}$, $\quad\vc = -\vw$
Vektoreiden erotus
MÄÄRITELMÄ: EROTUS
Vektoreiden $\vv$ ja $\vw$ erotus $\vv-\vw$ saadaan lisäämällä vektoriin $\vv$ vastavektori $-\vw$.
Palautetaan mieleen, että summan $\bar{v}+\bar{w}$ voi määrittää piirtämällä seuraavasti: piirretään vektori $\bar{v}$ ja piirretään sen perään vektori $\bar{w}$ alkamaan vektorin $\bar{v}$ loppupisteestä. Summa $\bar{v}+\bar{w}$ on vektori, joka alkaa vektorin $\bar{v}$ alkupisteestä ja päättyy vektorin $\bar{w}$ loppupisteeseen. Tätä on havainnollistettu alla olevassa kuvassa.
Erotuksen $\bar{v}-\bar{w}$ voi määrittää piirtämällä samaan tapaan vektoreiden $\vv$ ja $-\vw$ avulla. Piirretään vektori $\bar{v}$ ja piirretään sen perään vastavektori $-\bar{w}$ alkamaan vektorin $\bar{v}$ loppupisteestä. Erotus $\bar{v}-\bar{w}$ on vektori, joka alkaa vektorin $\bar{v}$ alkupisteestä ja päättyy vektorin $-\bar{w}$ loppupisteeseen.
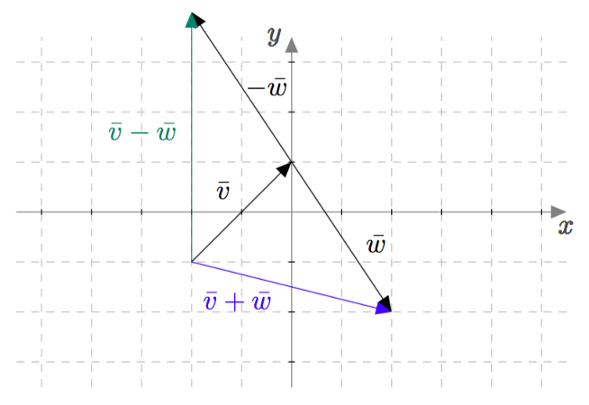
Vektoreiden erotus lasketaan samaan tapaan komponenteittain kuin summakin. Esimerkiksi yllä olevan kuvan vektoreiden $\vv$ ja $\vw$ erotus on \begin{align*} \vv-\vw &=2\vi+2\vj-(2\vi - 3\vj) \\ &=2\vi+2\vj-2\vi + 3\vj \\ &=0\vi + 5\vj \\ &=5\vj. \end{align*}
Vektoreiden erotus
Tutki vektoreita $\va=-3\vi+4\vj$ ja $\vb=5\vi+2\vj$.
- Laske erotus $\va-\vb$.
- Määritä erotus $\va-\vb$ piirtämällä vektoreiden $\va$ ja $-\vb$ avulla.
- Vertaa a- ja b-kohtien tuloksia. Ovatko ne sopusoinnussa keskenään?
VASTAUS
- $-8\vi + 2\vj$
Kahden pisteen välinen vektori
Edellä tutustuttiin paikkavektorin käsitteeseen: pisteen $P$ paikkavektori $\pv{OP}$ tarkoittaa vektoria, jonka alkupiste on origo $O$ ja loppupiste on piste $P$. Myös muita vektoreita voidaan merkitä samaan tapaan alkupisteen ja loppupisteen avulla. Merkintä $\pv{AB}$ tarkoittaa vektoria, jonka alkupiste on $A$ ja loppupiste on $B$. Esimerkiksi alla olevassa kuvassa $\pv{AB} = 4\vi + 2\vj$ ja $\pv{RS} = \vi - 3\vj$. Lisäksi havaitaan, että vektori $\pv{CD}$ on sama kuin vektori $\pv{AB}$ eli $\pv{CD} = \pv{AB}$, sillä ne voidaan ilmaista samalla tavalla vektoreiden $\vi$ ja $\vj$ avulla.
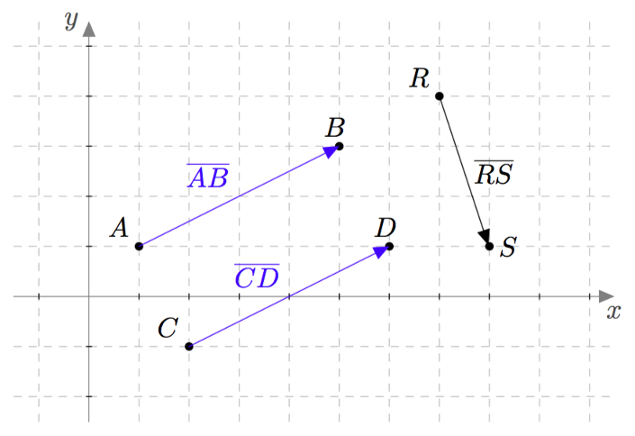
Kahden pisteen välinen vektori
Tarkastele alla olevaa kuvaa.
- Muodosta pisteiden $A$ ja $B$ paikkavektorit $\pv{OA}$ ja $\pv{OB}$.
- Millä laskutoimituksella saat niistä muodostettua vektorin $\pv{AB}$?
- Muodosta pisteiden $C$ ja $D$ paikkavektorit $\pv{OC}$ ja $\pv{OD}$.
- Millä laskutoimituksella saat niistä muodostettua vektorin $\pv{CD}$?
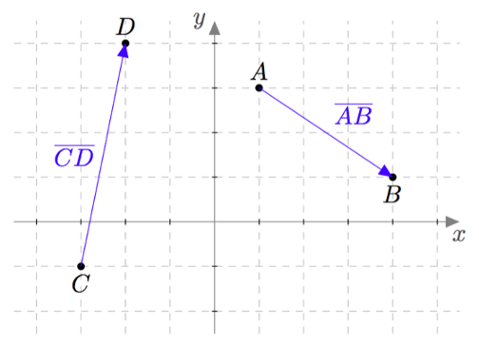
VASTAUS
- $\pv{OA} = \vi + 3\vj$ ja $\pv{OB} = 4\vi + \vj$
- $\pv{OC} = -3\vi - \vj$ ja $\pv{OD} = -2\vi + 4\vj$
Kuten edellisessä tehtävässä huomataan, vektori $\pv{AB}$ saadaan muodostettua paikkavektoreiden $\pv{OA}$ ja $\pv{OB}$ avulla. Tätä varten täytyy etsiä reitti vektorin $\pv{AB}$ alkupisteestä sen loppupisteeseen. Alkupisteestä $A$ päästään origoon paikkavektorin vastavektorilla $-\pv{OA}$. Origosta päästään pisteeseen $B$ paikkavektorilla $\pv{OB}$. Tätä on havainnollistettu alla olevassa kuvassa.
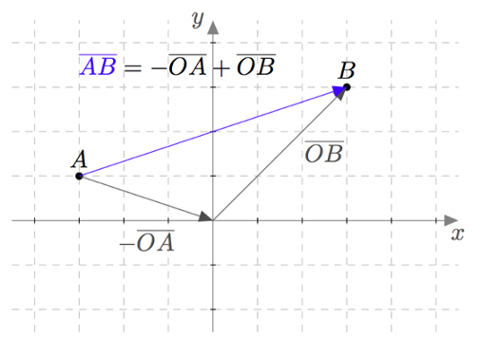
Vektori $\pv{AB}$ saadaan siis laskemalla yhteen vektorit $-\pv{OA}$ ja $\pv{OB}$. Toisin sanottuna $$\pv{AB} = -\pv{OA}+\pv{OB}$$ eli $$\pv{AB} = \pv{OB}-\pv{OA}.$$ Yllä olevan kuvan tilanteessa $$ \begin{align*} \pv{AB} &= (3\vi + 3\vj)-(-3\vi + \vj)\\ &=6\vi + 2\vj. \end{align*} $$
Kahden pisteen välinen vektori
Merkitään $A = (-4,1)$ ja $B = (2,-3)$.
- Ilmaise paikkavektorit $\pv{OA}$ ja $\pv{OB}$ vektoreiden $\vi$ ja $\vj$ avulla.
- Määritä vektori $\pv{AB}$ käyttäen hyväksi a-kohdan tuloksia.
- Miten vektorin $\pv{AB}$ voisi päätellä suoraan pisteiden $A$ ja $B$ koordinaateista? Selitä omin sanoin.
VASTAUS
- $\pv{OA} = -4\vi + \vj$ ja $\pv{OB} = 2\vi - 3\vj$
- $\pv{AB} = 6\vi - 4\vj$
Tiedetään, että pisteen paikkavektoreissa vektoreiden $\vi$ ja $\vj$ kertoimet ovat samat kuin pisteen koordinaatit. Tämän vuoksi kahden pisteen välisessä vektorissa vektoreiden $\vi$ ja $\vj$ kertoimiksi saadaan vektorin loppupisteen ja alkupisteen koordinaattien erotus. Tätä on havainnollistettu alla olevassa kuvassa.
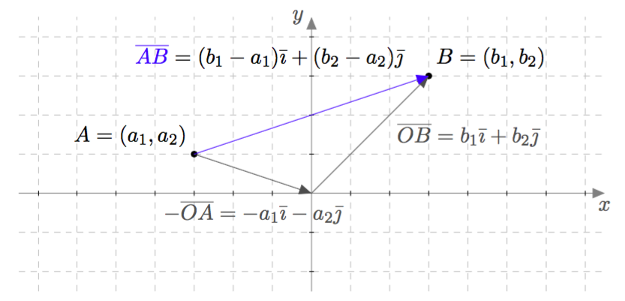
Kahden pisteen välinen vektori
Merkitään $A = (-12,17)$, $B = (35,11)$, $C = (26,-29)$, $D = (-14,36)$, $E = (10,43)$ ja $F = (58,13)$.
- Ilmaise vektorit $\pv{AB}$ ja $\pv{CD}$ vektoreiden $\vi$ ja $\vj$ avulla. Tarkista tulosten järkevyys hahmottelemalla mallikuva tilanteesta.
- Ilmaise vektorit $\pv{DA}$ ja $\pv{EF}$ vektoreiden $\vi$ ja $\vj$ avulla. Tarkista tulosten järkevyys hahmottelemalla mallikuva tilanteesta.
VASTAUS
- $\pv{AB} = 47\vi - 6\vj$ ja $\pv{CD} = -40\vi + 65\vj$
- $\pv{DA} = 2\vi - 19\vj$ ja $\pv{EF} = 48\vi-30\vj$
Vektorin suunta ja pituus
Tutkitaan seuraavaksi vektoreiden suuntia. Alla olevan kuvan vektorit $\va$ ja $\vv$ ovat samansuuntaiset. Myös esimerkiksi vektorit $-\va$ ja $\vu$ ovat samansuuntaiset. Tämä voidaan merkitä kirjoittamalla $\va \upuparrows \vv$ ja $-\va \upuparrows \vu$.
Vektorit $-3\va$ ja $\vw$ ovat puolestaan vastakkaissuuntaiset. Tämä voidaan merkitä kirjoittamalla $-3\va \uparrow\downarrow \vw$.
Vektorit, jotka ovat joko saman- tai vastakkaisuuntaiset, ovat yhdensuuntaiset. Kaikki alla olevan kuvan vektorit ovat yhdensuuntaisia. Esimerkiksi vektorit $\va$ ja $-3\va$ ovat yhdensuuntaiset, mikä voidaan merkitä kirjoittamalla $\va \parallel -3\va$.
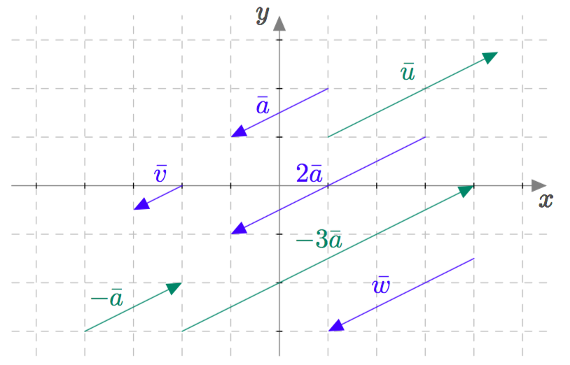
Vektoreiden yhdensuuntaisuus
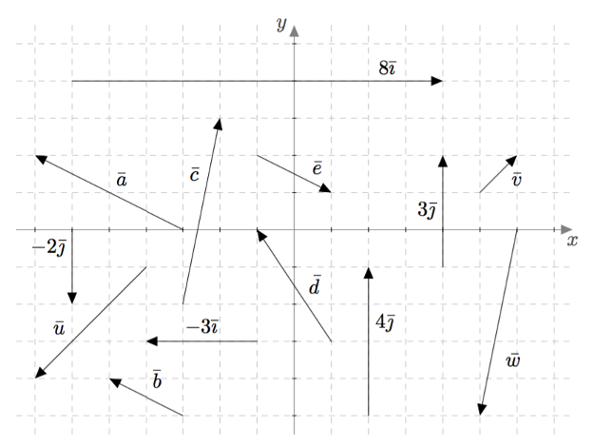
Tarkastele alla olevaa kuvaa. Kirjoita vastauksesi käyttäen yllä esiteltyjä merkintöjä $\upuparrows$ ja $\uparrow\downarrow$.
- Mitkä vektorit ovat samansuuntaisia?
- Mitkä vektorit ovat vastakkaissuuntaisia?
- Mitkä vektorit eivät ole yhdensuuntaisia minkään muun kuvassa näkyvän vektorin kanssa?
VASTAUS
- $\va$ ja $\vb$; $\quad 3\vj$ ja $4\vj$
- $\va$ ja $\bar{e}$; $\quad \vb$ ja $\bar{e}$; $\quad \vc$ ja $\vw$; $\quad \vu$ ja $\vv$; $\quad -3\vi$ ja $8\vi$; $\quad -2\vj$ ja $3\vj$; $\quad -2\vj$ ja $4\vj$
- $\bar{d}$
Vektoreiden yhdensuuntaisuus
- Millaisella luvulla kertominen säilyttää vektorin suunnan?
- Millaisella luvulla vektoria pitää kertoa, jotta sen suunta muuttuu vastakkaiseksi?
MÄÄRITELMÄ: YHDENSUUNTAISUUS
Vektorit $\vv$ ja $\vw$ ovat yhdensuuntaiset eli $\vv \parallel \vw$, jos ja vain jos $\vv=r\vw$ jollakin reaaliluvulla $r \neq 0$.
Esimerkiksi vektorit $\va=4\vi+6\vj$ ja $\vb=-2\vi-3\vj$ ovat yhdensuuntaiset, sillä \begin{align*} \va &=4\vi+6\vj \\ &=-2(-2\vi-3\vj) \\ &=-2\vb. \end{align*} Yllä vektoreiden yhdensuuntaisuus osoitettiin muokkaamalla vektoria $\va$ niin, että se saatiin ilmoitettua vektorin $\vb$ skalaarimonikertana eli muodossa $t\vb$, missä $t \in \R$. Toinen tapa tutkia vektoreiden yhdensuuntaisuutta on muodostaa yhtälö $\va=t\vb$ ja tutkia, toteutuuko tämä yhtälö jollakin luvulla $t \neq 0$. Jos ratkaisu löytyy, vektorit ovat yhdensuuntaiset. Esimerkiksi edellisessä tilanteessa ratkaisu on $t = -2$. Jos ratkaisua ei löydy, niin vektorit eivät ole yhdensuuntaiset.
Vektoreiden yhdensuuntaisuus
Tarkastele vektoria $\vv=-5\vi-5\vj$.
- Muodosta kaksi uutta vektoria, jotka ovat vektorin $\vv$ kanssa yhdensuuntaisia.
- Onko vektori $\vw=\vi+\vj$ yhdensuuntainen vektorin $\vv$ kanssa?
- Onko vektori $\vu=\vi+2\vj$ yhdensuuntainen vektorin $\vv$ kanssa?
Vektorin pituus saadaan laskettua Pythagoraan lauseen avulla. Esimerkiksi alla olevassa kuvassa vektorin $\va$ pituus $\left|\va\right|$ saadaan yhtälöstä $$ \left|\va\right|^2 = 2^2 + 3^2. $$ Vektorin $\va$ pituudeksi saadaan siis $$ \left|\va\right| = \sqrt{2^2 + 3^2}=\sqrt{4+9}=\sqrt{13} \approx 3{,}6. $$
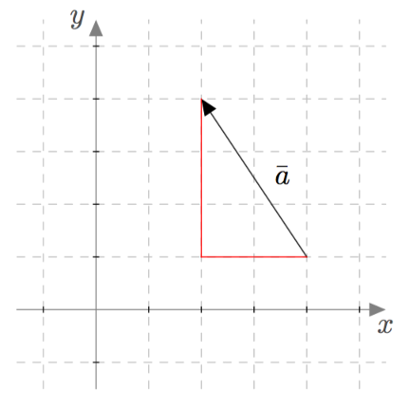
Koska toiseen potenssiin korotus tekee kaikista luvuista epänegatiivisia, voidaan vektorin pituus määritellä seuraavasti:
MÄÄRITELMÄ: VEKTORIN PITUUS
Vektorin $\vv=x\vi+y\vj$ pituus on $$|\vv|=\sqrt{x^2+y^2}.$$
Huomaa, että merkintä $|\vv|$ tarkoittaa vektorin $\vv$ pituutta, kun taas merkintä $|x|$ tarkoittaa luvun $x$ itseisarvoa.
Vektorin pituus
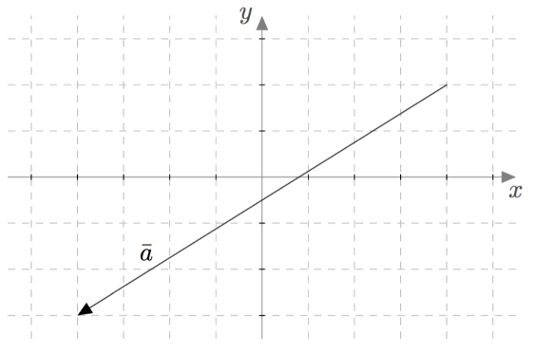
Tutki kuvassa näkyvää vektoria $\va$.
- Lausu vektori $\va$ vektoreiden $\vi$ ja $\vj$ avulla.
- Laske vektorin $\va$ pituus.
VASTAUS
- $\va = -8\vi - 5\vj$
- $|\va| = \sqrt{89} \approx 9{,}4$
Vektorin pituus
Laske tai päättele vektoreiden $\vi$ ja $\vj$ pituus.
Vektorin pituus
Piirrä vektorit $\vv = -2\vi + 5\vj$ ja $\vw = 7\vi - 4\vj$ koordinaatistoon ja laske niiden pituus.
VASTAUS
$|\vv| = \sqrt{29}$ ja $|\vw| = \sqrt{65}$
TEOREEMA
Kaksi vektoria ovat samat, jos ja vain jos ne ovat samansuuntaiset ja yhtä pitkät.
Perustelu:
- Se, että kaksi vektoria ovat samat, tarkoittaa, että ne voidaan esittää samalla tavalla vektoreiden $\vi$ ja $\vj$ avulla. Tällöin ne ovat samansuuntaiset ja yhtä pitkät.
- Jos vektorit ovat samansuuntaiset ja yhtä pitkät, ne voidaan esittää samalla tavalla vektoreiden $\vi$ ja $\vj$ avulla. Tämä tarkoittaa, että ne ovat samat.
Vektorin pituus
Tutki vektoria $\vv=6\vi+3\vj$.
- Muodosta vektorit $5\vv$, $-2\vv$ ja $\frac{1}{3}\vv$.
- Laske vektoreiden $\vv$, $5\vv$, $-2\vv$ ja $\frac{1}{3}\vv$ pituudet.
- Selitä omin sanoin, miten vektorin kertominen luvulla vaikuttaa vektorin pituuteen.
- Millaisella luvulla vektoria tulee kertoa, jotta se pitenee?
- Millaisella luvulla vektoria tulee kertoa, jotta se lyhenee?
VASTAUS
- $5\vv=30\vi+15\vj$, $-2\vv=-12\vi-6\vj$, $\frac{1}{3}\vv=2\vi+\vj$
- $|\vv| = \sqrt{45} = 3\sqrt{5}$, $|5\vv| = 15\sqrt{5}$, $|-2\vv| = 6\sqrt{5}$, $|\frac{1}{3}\vv| = \sqrt{5}$
Tarkastellaan alla olevan kuvan vektoreiden $\va=2\vi+\vj$ ja $-4\va=-8\vi-4\vj$ pituuksia. Huomataan, että vektorin $\va$ pituus on $$ \begin{align*} |\va|&=\sqrt{2^2+1^2} \\ &= \sqrt{4+1} \\ &=\sqrt{5} \end{align*} $$ ja vektorin $-4\va$ pituus on $$ \begin{align*} |-4\va|&=\sqrt{(-8)^2+(-4)^2} \\ &= \sqrt{64+16} \\ &=\sqrt{80} \\ &= \sqrt{16\cdot 5} \\ &=\sqrt{16} \cdot \sqrt{5} \\ &=4\sqrt{5} \\ &=4\cdot |\va|\\ &=|-4|\cdot |\va|. \end{align*} $$
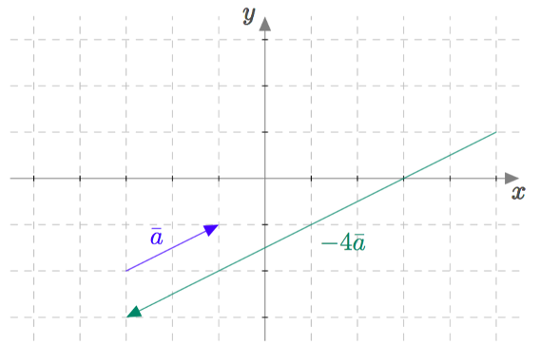
Voidaan näyttää, että tämä pätee kaikille vektoreille: Vektorin $t\vv$ pituus $|t\vv|$ saadaan kertomalla vektorin $\vv$ pituutta luvun $t$ itseisarvolla. Tämä teoreema perustellaan myöhemmin $xyz$-koordinaatistoa käsittelevässä luvussa.
TEOREEMA
Kaikilla vektoreilla $\vv$ ja reaaliluvuilla $t$ pätee, että $$|t\vv|=|t|\cdot |\vv|.$$
MÄÄRITELMÄ: YKSIKKÖVEKTORI
Vektoria, jonka pituus on $1$, sanotaan yksikkövektoriksi.
Tehtävän 25 mukaan vektorit $\vi$ ja $\vj$ ovat yksikkövektoreita, sillä niiden pituus on $1$. Niiden lisäksi on paljon muitakin yksikkövektoreita. Perehdytään seuraavaksi siihen, miten voidaan määrittää annetun vektorin suuntainen yksikkövektori.
Tarkastellaan alla olevan kuvan vektoria $\vv = 8\vi + 6\vj$. Sen pituudeksi saadaan $$ \begin{align*} |\vv| &= \sqrt{8^2+6^2} \\ &= \sqrt{100} \\ &= 10. \end{align*} $$ Vektorin $\vv$ kanssa samansuuntainen yksikkövektori saadaan ottamalla siitä kymmenesosa, eli $$ \begin{align*} \frac{1}{10}\vv &= \frac{1}{10}(8\vi + 6\vj) \\ &= 0{,}8\vi + 0{,}6\vj \end{align*} $$
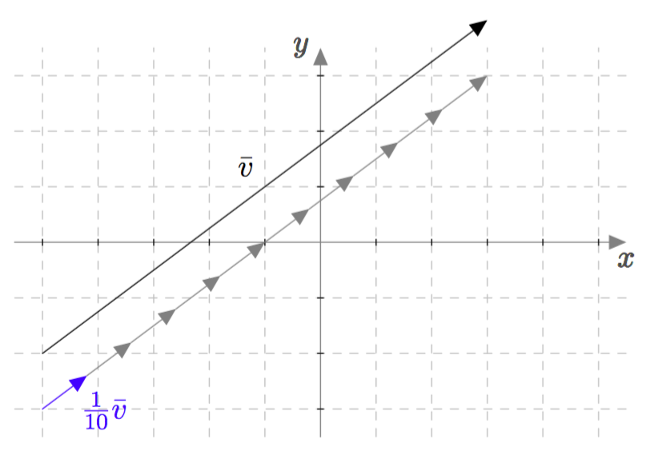
Yksikkövektori
Tutki vektoria $\vb = 3\vi - 4\vj$.
- Laske vektorin $\vb$ pituus.
- Määritä vektorin $\vb$ kanssa samansuuntainen vektori, jonka pituus on $10$. Piirrä se koordinaatistoon.
- Määritä vektorin $\vb$ kanssa samansuuntainen yksikkövektori eli vektori, joka pituus on $1$. Piirrä se koordinaatistoon.
- Määritä vektorin $\vb$ kanssa vastakkaissuuntainen yksikkövektori. Piirrä se koordinaatistoon.
VASTAUS
- $|\vb| = 5$
- $2\vb = 6\vi - 8\vj$
- $\frac{1}{5}\vb = \frac{3}{5}\vi - \frac{4}{5}\vj$
- $-\frac{1}{5}\vb = -\frac{3}{5}\vi + \frac{4}{5}\vj$
Vektorin jakaminen komponentteihin
Edellä opittiin ilmaisemaan $xy$-tason vektoreita vektoreiden $\vi$ ja $\vj$ avulla. Esimerkiksi alla olevan kuvan vektori $\va$ voidaan kirjoittaa muodossa $\va = 6\vi + 3\vj$. Yhteenlaskettavia $6\vi$ ja $3\vj$ kutsutaan vektorin $\va$ komponenteiksi.
Vektori $\va$ voidaan jakaa komponentteihin muillakin tavoilla. Alla olevasta kuvasta nähdään, että vektori $\va$ voidaan kirjoittaa myös muodossa $\va = 5\vv + 4\vw$, missä $\vv = 2\vi-\vj$ ja $\vw = -\vi+2\vj$. Sanotaan, että $5\vv$ ja $4\vw$ ovat vektorin $\va$ vektorien $\vv$ ja $\vw$ suuntaiset komponentit.
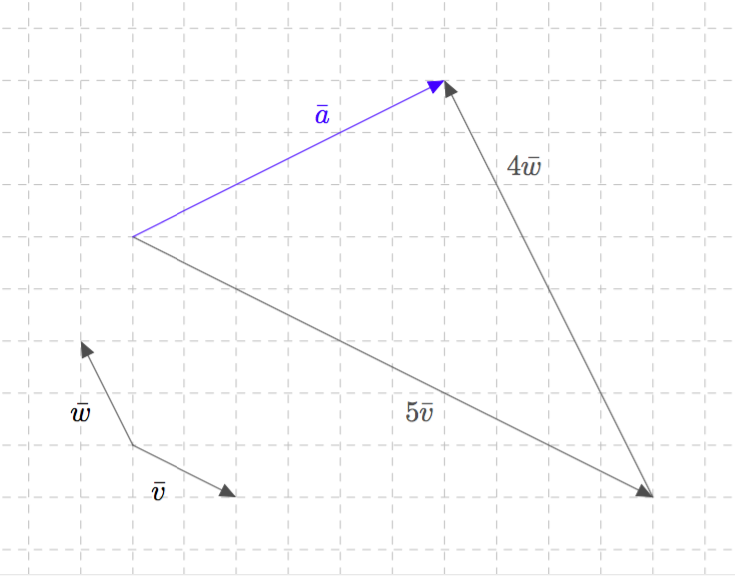
MÄÄRITELMÄ: VEKTORIN KOMPONENTIT
Oletetaan, että $\vv$ ja $\vw$ ovat kaksi vektoria, joista kumpikaan ei ole nollavektori. Oletetaan lisäksi, että vektorit $\vv$ ja $\vw$ eivät ole yhdensuuntaiset.
Jos vektori $\va$ voidaan kirjoittaa muodossa $$\va = s\vv + t\vw$$ missä $s$ ja $t$ ovat reaalilukuja, niin sanotaan, että $s\vv$ ja $t\vw$ ovat vektorin $\va$ vektoreiden $\vv$ ja $\vw$ suuntaiset komponentit.
Vektorin jakaminen komponentteihin
Jaa vektori $\va = 6\vi + 3\vj$ vektoreiden $\vb$ ja $\vc$ suuntaisiin komponentteihin kuvan avulla päättelemällä,
- jos $\vb = \vi + 2\vj$ ja $\vc = \vi-\vj$.
- jos $\vb = \vi - 2\vj$ ja $\vc = \vi+\vj$.
VASTAUS
- $\va = 3\vb + 3\vc$, joten kysytyt komponenttivektorit ovat $3\vb$ ja $3\vc$
- $\va = \vb + 5\vc$, joten kysytyt komponenttivektorit ovat $\vb$ ja $5\vc$
Vektoreiden pistetulo ja vektoreiden välinen kulma
MÄÄRITELMÄ: PISTETULO
Vektoreiden $\vv=x_1\vi+y_1\vj$ ja $\vw=x_2\vi+y_2\vj$ pistetulo on $$\vv \cdot \vw = x_1x_2+y_1y_2.$$
Vektoreiden pistetulosta saadaan siis tuloksena aina reaaliluku. Esimerkiksi vektoreiden $\vv=-2\vi+4\vj$ ja $\vw=3\vi-\vj$ pistetulo on \begin{align*} \vv \cdot \vw &= (-2\vi+4\vj) \cdot (3\vi-\vj) \\ &= (-2) \cdot 3 + 4\cdot (-1) \\ &= -6-4 \\ &=-10. \end{align*} Reaalilukuja voidaan kutsua skalaareiksi, minkä vuoksi pistetuloa kutsutaan joskus skalaarituloksi.
Pistetulo
Tarkaste vektoreita $\va=7\vi+6\vj$, $\vb=3\vi-5\vj$ ja $\vc=5\vi+3\vj$.
- Piirrä vektorit $\va$, $\vb$ ja $\vc$ koordinaatistoon niin, että ne alkavat samasta pisteestä.
- Laske pistetulo $\va \cdot \vb$.
- Laske pistetulo $\va \cdot \vc$.
- Laske pistetulo $\vb \cdot \vc$.
- Millaisessa tilanteessa vektoreiden pistetulo on nolla? Vertaa edellisten laskujen tuloksia ja piirtämääsi kuvaa.
VASTAUS
- $\va \cdot \vb = -9$
- $\va \cdot \vc = 53$
- $\vb \cdot \vc = 0$
Pistetulo
Tarkastele vektoreita $\va=-11\vi+5\vj$, $\vb=-4\vi-7\vj$ ja $\vc=3\vi-9\vj$ sekä reaalilukua $t=3$.
- Laske pistetulot $\va \cdot \vb$ ja $\va \cdot \vc$.
- Laske pistetulo $\va \cdot (\vb + \vc)$.
- Vertaa a- ja b-kohtien tuloksia. Miten ne liittyvät toisiinsa?
- Laske pistetulot $(t\va) \cdot \vb$ ja $\va \cdot (t\vb)$.
- Vertaa a- ja d-kohtien tuloksia. Millaisen ilmiön huomaat?
Pistetulolla voidaan laskea tavallisten laskusääntöjen mukaan. Näitä on koottu alla olevaan teoreemaan.
TEOREEMA
Olkoot $\va$, $\vb$ ja $\vc$ vektoreita ja $t$ reaaliluku. Pistetulolla on seuraavat ominaisuudet:
- vaihdannaisuus: $\va \cdot \vb = \vb \cdot \va$
- osittelulaki: $\va \cdot (\vb + \vc) =(\va \cdot \vb) + (\va \cdot \vc)$
- skalaarin siirto: $t(\va \cdot \vb) =(t\va) \cdot \vb = \va \cdot (t\vb)$
Perustelu: Merkitään $\va = x_1\vi + y_1\vj$ ja $\vb = x_2\vi+y_2\vj$.
- Pistetulon määritelmän mukaan $\va \cdot \vb = x_1x_2 + y_1y_2$ ja $\vb \cdot \va = x_2x_1+y_2y_1$. Koska $x_1$ ja $x_2$ sekä $y_1$ ja $y_2$ ovat reaalilukuja, voi niiden järjestyksen kertolaskussa vaihtaa. Siis $x_1x_2 = x_2x_1$ ja $y_1y_2 = y_2y_1$. Tästä seuraa, että $\va \cdot \vb = \vb \cdot \va$.
Ominaisuudet 2. ja 3. voidaan perustella samaan tapaan.
Pistetulon ja vektorin pituuden yhteys
Tarkastele vektoria $\va=-6\vi+8\vj$.
- Laske pistetulo $\va \cdot \va$.
- Laske vektorin $\va$ pituus.
- Vertaa a- ja b-kohtien tuloksia. Miten ne liittyvät toisiinsa?
VASTAUS
- $\va \cdot \va = 100$
- $|\va| = 10$
Pistetulon ja vektorin pituuden yhteys
Tarkastele vektoria $\vv=x\vi+y\vj$.
- Muodosta lauseke pistetulolle $\vv \cdot \vv$.
- Muodosta lauseke vektorin $\vv$ pituudelle $\left|\vv\right|$.
- Vertaa a- ja b-kohtien tuloksia. Miten ne liittyvät toisiinsa?
Edellisen tehtävän tuloksena saadaan seuraava teoreema:
TEOREEMA
Vektorin pistetulo itsensä kanssa on yhtä suuri kuin vektorin pituuden neliö. Toisin sanottuna $\vv \cdot \vv = \left|\vv\right|^2$
Tutkitaan seuraavaksi vektoreiden välisen kulman ja pistetulon yhteyttä. Vektoreiden välistä kulmaa voidaan tarkastella, jos vektoreiden alkupisteet ovat samat. Vektoreiden välisellä kulmalla tarkoitetaan muodostuvista kulmista pienempää. Tätä on havainnollistettu alla olevassa kuvassa.
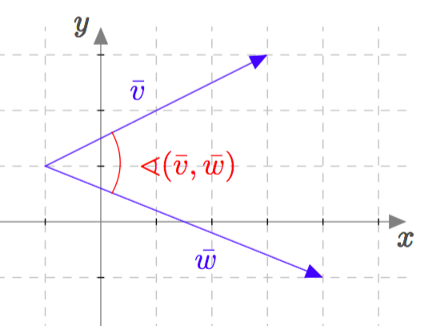
Vektoreiden $\vv$ ja $\vw$ väliselle kulmalle käytetään merkintää $\sphericalangle(\vv,\vw)$ kuten yllä olevassa kuvassa. Joskus käytetään myös lyhyttä merkintää $(\vv,\vw)$.
Vektoreiden välinen kulma
Tarkastele yllä olevaa kuvaa.
- Kuinka suuri on vektoreiden $\vv$ ja $2\vv$ välinen kulma?
- Kuinka suuri on vektoreiden $\vv$ ja $-\vv$ välinen kulma
- Jos vektorit ovat samansuuntaiset, mikä niiden välinen kulma on
- Jos vektorit ovat vastakkaissuuntaiset, mikä niiden välinen kulma on
VASTAUS
- $0^\circ$
- $180^\circ$
Vektoreiden välinen kulma
Tarkastele alla olevaa kuvaa. Siirrä vektorit tarvittaessa alkamaan samasta pisteestä. Kuinka suuri on vektoreiden
- $\va$ ja $\vb$ välinen kulma $\sphericalangle(\va,\vb)$
- $\va$ ja $\vc$ välinen kulma $\sphericalangle(\va,\vc)$
- $\vb$ ja $\vc$ välinen kulma $\sphericalangle(\vb,\vc)$?
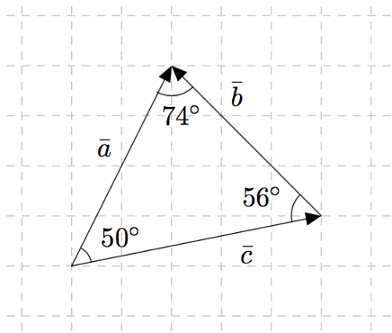
VASTAUS
- $74^\circ$
- $50^\circ$
- $124^\circ$
Geometria-kurssista tutun kosinilauseen ja pistetulon ominaisuuksien avulla saadaan perusteltua seuraava teoreema, joka yhdistää pistetulon ja vektoreiden välisen kulman. Teoreema perustellaan myöhemmin $xyz$-koordinaatistoa käsittelevässä luvussa.
TEOREEMA
Vektoreiden $\vv$ ja $\vw$ pistetulolle pätee $$\vv \cdot \vw = |\vv||\vw|\cos (\vv, \vw).$$
Jos $\vv \neq \bar{0}$ ja $\vw \neq \bar{0}$, niin vektoreiden $\vv$ ja $\vw$ välinen kulma $(\vv, \vw)$ saadaan yhtälöstä $$ \cos (\vv, \vw)=\frac{\vv \cdot \vw}{|\vv||\vw|}. $$
Edellisen teoreeman merkintä $\cos(\vv, \vw)$ tarkoittaa siis vektoreiden $\vv$ ja $\vw$ välisen kulman kosinia.
Pistetulo
Vektorin $\va$ pituus on $\left|\va\right| = 3$ ja vektorin $\vb$ pituus on $\left|\vb\right| = 7$. Laske edellisen teoreeman avulla pistetulo $\va \cdot \vb$, jos
- vektorit $\va$ ja $\vb$ ovat samansuuntaiset.
- vektorit $\va$ ja $\vb$ ovat vastakkaissuuntaiset.
- vektoreiden $\va$ ja $\vb$ välinen kulma on $45^{\circ}$.
- vektoreiden $\va$ ja $\vb$ välinen kulma on $135^{\circ}$.
- vektoreiden $\va$ ja $\vb$ välinen kulma on $90^{\circ}$.
VASTAUS
- $\va \cdot \vb = 21$
- $\va \cdot \vb = -21$
- $\va \cdot \vb = \frac{21}{\sqrt{2}} = \frac{21}{2}\sqrt{2}$
- $\va \cdot \vb = -\frac{21}{\sqrt{2}} = -\frac{21}{2}\sqrt{2}$
- $\va \cdot \vb = 0$
Pistetulo ja vektoreiden välinen kulma
Tarkaste kolmiota $ABC$, missä $\overline{AB}=5\vi-4\vj$ ja $\overline{AC}=9\vi+3\vj$.
- Laske kolmion kulmien suuruudet asteen tarkkuudella.
- Piirrä kuva kolmiosta $ABC$ ja tarkista, onko vastauksesi järkevä.
VASTAUS
- Kulma $A$ noin $57^\circ$, kulma $B$ noin $81^\circ$ ja kulma $C$ noin $42^\circ$.
Pistetulon avulla voidaan tarkistaa, ovatko vektorit kohtisuorassa toisiaan vastaan.
TEOREEMA
Oletetaan, että $\vv \neq \bar{0}$ ja $\vw \neq \bar{0}$. Vektorit $\vv$ ja $\vw$ ovat toisiaan vastaan kohtisuorassa, jos ja vain jos $\vv \cdot \vw = 0$.
Perustelu:
- Oletetaan, että vektorit $\vv$ ja $\vw$ ovat kohtisuorassa toisiaan vastaan eli $\sphericalangle(\vv,\vw)=90^{\circ}$. Tällöin \begin{align*} \vv \cdot \vw &= |\vv||\vw|\cos (\vv, \vw) \\ &= |\vv||\vw|\cos 90^{\circ} \\ &= |\vv||\vw| \cdot 0 \\ &= 0. \end{align*} Siis $\vv \cdot \vw = 0$.
- Oletetaan, että $\vv \cdot \vw = 0$. Tiedetään, että $\vv \cdot \vw = |\vv||\vw|\cos (\vv, \vw)$. Näistä tiedoista voidaan päätellä, että $|\vv||\vw|\cos (\vv, \vw) = 0$. Oletuksen mukaan $\vv \neq \bar{0}$ ja $\vw \neq \bar{0}$, joten vektoreiden $\vv$ ja $\vw$ pituudet ovat positiivisia: $\left|\vv\right| > 0$ ja $\left|\vw\right| > 0$. Tulon nollasäännön avulla voidaan siten päätellä, että $\cos (\vv, \vw) = 0$. Tästä seuraa, että $\sphericalangle(\vv,\vw)=90^{\circ}$. Vektorit $\vv$ ja $\vw$ ovat siis toisiaan vastaan kohtisuorassa.
Pistetulo ja vektoreiden kohtisuoruus
Tutki vektoreita $\vv=-2\vi+3\vj$ ja $\vw=x\vi+3\vj$.
- Muodosta lauseke pistetulolle $\vv \cdot \vw$.
- Millä muuttujan $x$ arvolla vektorit $\vv$ ja $\vw$ ovat kohtisuorassa toisiaan vastaan?
- Piirrä vektorit $\vv$ ja $\vw$ koordinaatistoon ja tarkista, onko vastauksesi järkevä.
VASTAUS
- $-2x+9$
- $x = 4{,}5$
TEHTÄVÄSARJA II
Vektorin esittäminen vektoreiden $\vi$ ja $\vj$ avulla
Tarkastele alla olevan kuvan vektoreita. Mitkä niistä voidaan esittää muodossa $2\vi+\vj$?
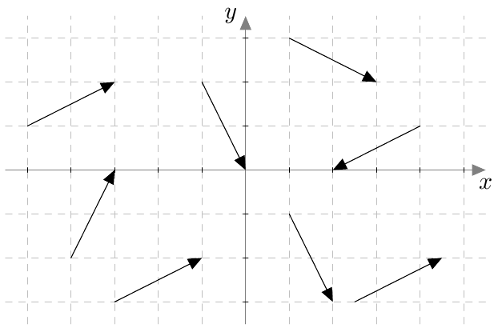
VASTAUS
Ne kolme vektoria, jotka osoittavat suunnan kaksi askelta oikealle ja yksi ylös (kuvassa vasemmalla ja alalaidassa).
Vektoreiden samuus
Päättele, millä reaaliluvuilla $r$ ja $s$ vektorit $\vv=-r\vi+8\vj$ ja $\vw=5\vi-12s\vj$ ovat samat. Selitä, miten päättelit.
VASTAUS
$r = -5$ ja $s = -\frac{2}{3}$
Paikkavektori
Määritä pisteen $P$ koordinaatit, jos
- $\pv{OP}=\vi+2\vj$
- $\pv{OP}=3\vi-4\vj$
- $\pv{OP}=-\vj$.
VASTAUS
- $P = (1,2)$
- $P = (3,-4)$
- $P = (0,-1)$.
Vektoreiden laskutoimituksia
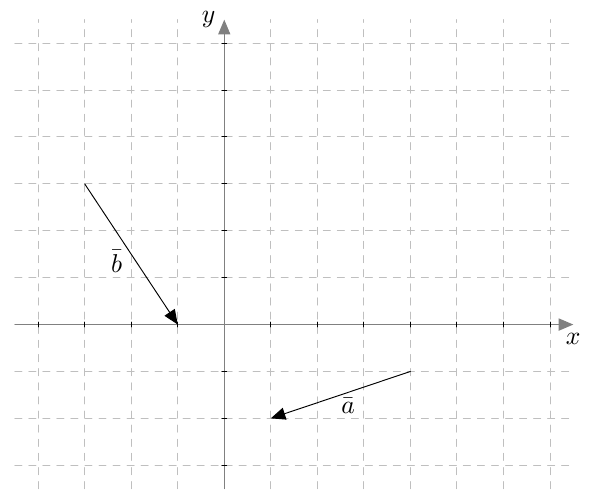
Tarkastele alla olevaa kuvaa. Päättele kuvan avulla, mihin pisteeseen päädyt, kun lähdet pisteestä $(2,3)$ ja siirryt
- vektorin $\va$ verran
- ensin vektorin $\va$ verran ja sitten vektorin $\vb$ verran
- vektorin $-\vb$ verran
- ensin vektorin $-\va$ verran ja sitten vektorin $\vb$ verran.
VASTAUS
- pisteeseen $(-1,2)$
- pisteeseen $(1,-1)$
- pisteeseen $(0,6)$
- pisteeseen $(7,1)$
Vektoreiden summa ja erotus
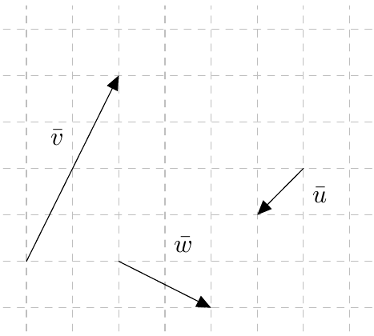
Tarkastele alla olevaa kuvaa. Piirrä vektoreiden $\vv$, $\vw$ ja $\vu$ avulla vektorit
- $\vv+\vw$
- $\vw-\vv$
- $\vv-\vw-\vu$
- $\vv-\vw+\vu$
Vektorin kertominen luvulla
Tarkastele alla olevaan kuvaa. Ilmaise vektorit $\vb, \vc, \bar{d}$ ja $\bar{e}$ vektorin $\va$ avulla.
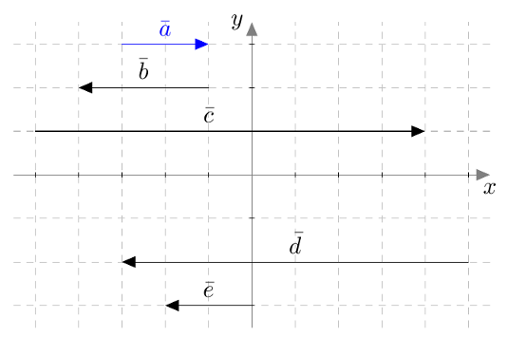
VASTAUS
$\vb = -\frac{3}{2}\va$, $\quad \vc = \frac{9}{2}\va$, $\quad \bar{d} = -4\va$, $\quad \bar{e} = -\va$
Vektoreiden summa ja erotus
Tarkastele vektoreita $\vv=-2\vi+7\vj$, $\vw=6\vi-10\vj$ ja $\vu=-3\vi+5\vj$. Määritä
- $(\vv+\vw)-(\vw+\vu)$
- $(\vv+\vw)-(\vv-\vu)-(\vw+\vu)$.
VASTAUS
- $\vv-\vu = \vi + 2\vj$
- $\bar{0}$
Paikkavektori
Tutki vektoria $\pv{AB}=-9\vi+5\vj$. Määritä pisteen $B$ paikkavektori kuvan avulla päättelemällä tai laskemalla, jos
- piste $A=(11,2)$
- piste $A=(-8,-7)$.
VASTAUS
- $\pv{OB} = 2\vi + 7\vj$
- $\pv{OB} = -17\vi - 2\vj$
Kahden pisteen välinen vektori
Määritä vektori $\pv{AB}$ laskemalla tai kuvan avulla päättelemällä, jos
- $A=(-5,2)$ ja $B=(3,1)$
- $A=(3,-7)$ ja $B=(-4,8)$.
VASTAUS
- $\pv{AB} = 8\vi - \vj$
- $\pv{AB} = -7\vi + 15\vj$
Kahden pisteen välinen vektori
Tarkastele pisteitä $A=(-2,4)$, $B=(3,1)$ ja $C=(5,-3)$. Määritä piste $D$ laskemalla tai piirtämällä, jos
- $\pv{CD}=\pv{AB}$
- $\pv{DC}=\pv{AB}$
- $\pv{AD}=-\pv{AC}$
- $\pv{BC}=-\pv{AD}$.
VASTAUS
- $D = (10,-6)$
- $D = (0,0)$
- $D = (-9,11)$
- $D = (-4,8)$
Kahden pisteen välinen vektori
Tarkastele pisteitä $A=(-1,4)$, $B=(3,-2)$ ja $C=(-2,1)$.
- Piirrä koordinaatistoon vektori $\pv{AB}$.
- Lausu vektori $\pv{AB}$ paikkavektoreiden $\pv{OA}$ ja $\pv{OB}$ avulla.
- Sievennä edellisen kohdan lauseke muotoon, jossa vektoreiden $\vi$ ja $\vj$ kertoimet ovat pisteiden $A$ ja $B$ koordinaattien erotuksia.
- Määritä vektori $\pv{AC}$ suoraan käyttämällä tietoa, että vektoreiden $\vi$ ja $\vj$ kertoimet ovat vektorin loppupisteen ja alkupisteen koordinaattien erotuksia.
VASTAUS
- $\pv{AB} = \pv{OB} - \pv{OA}$
- $\pv{AB} = 4\vi - 6\vj$
- $\pv{AC} = -\vi - 3\vj$
Vektoreiden suunta
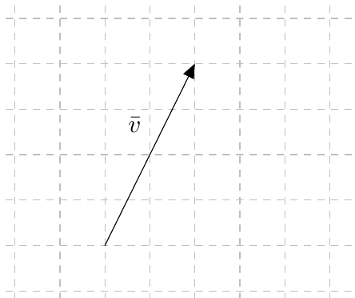
Tarkastele alla olevassa kuvassa olevaa vektoria $\vv$. Piirrä koordinaatisto ja siihen
- jokin vektori, joka on sama kuin $\vv$
- vektori, joka on vektorin $\vv$ kanssa samansuuntainen mutta kuitenkin eri vektori
- vektori, joka on vektorin $\vv$ kanssa yhdensuuntainen mutta ei samansuuntainen.
- jokin vektori, jonka pituus on 1,5 kertaa vektorin $\vv$ pituus ja joka ei ole vektorin $\vv$ kanssa yhdensuuntainen.
Vektoreiden yhdensuuntaisuus
Oletetaan, että kumpikaan vektoreista $\vv$ ja $\vw$ ei ole nollavektori. Tutki, ovatko vektorit $\vv$ ja $\vw$ yhdensuuntaiset, jos
- $\vv=6\vw$
- $2\vv+2\vw=14\vw-\vv$.
VASTAUS
- Kyllä.
- $\vv = 4\vw$, joten vektorit $\vv$ ja $\vw$ ovat yhdensuuntaiset.
Paikkavektori
Merkitään $A=(-5,2)$, $B=(-1,-1)$ ja $C=(2,1)$. Tiedetään, että vektorit $\pv{AB}$ ja $\pv{CD}$ ovat yhtä pitkät. Määritä piste $D$, jos vektorit $\pv{AB}$ ja $\pv{CD}$ ovat
- samansuuntaiset
- vastakkaissuuntaiset.
VASTAUS
- $D = (6,-2)$
- $D = (-2,4)$
Paikkavektori
Pisteen $A$ paikkavektori on $\pv{OA}=5\vi+12\vj$. Tiedetään, että $B=(-2,-5)$ ja $C=(2,-1)$.
- Vektori $\pv{BD}$ on samansuuntainen kuin vektori $\pv{OA}$ ja sen pituus on kaksi kertaa vektorin $\pv{OA}$ pituus. Päättele, mikä piste $D$ on. Selitä, miten ajattelit.
- Vektori $\pv{CE}$ on yhdensuuntainen vektorin $\pv{OA}$ kanssa ja sen pituus on puolet vektorin $\pv{OA}$ pituudesta. Mitä voit päätellä pisteestä $E$? Selitä, miten ajattelit.
VASTAUS
- $D = (8,19)$
- $E = \left(\frac{9}{2},5\right)\ $ tai $\ E = \left(-\frac{1}{2}, -7\right)$
Vektoreiden summa ja erotus
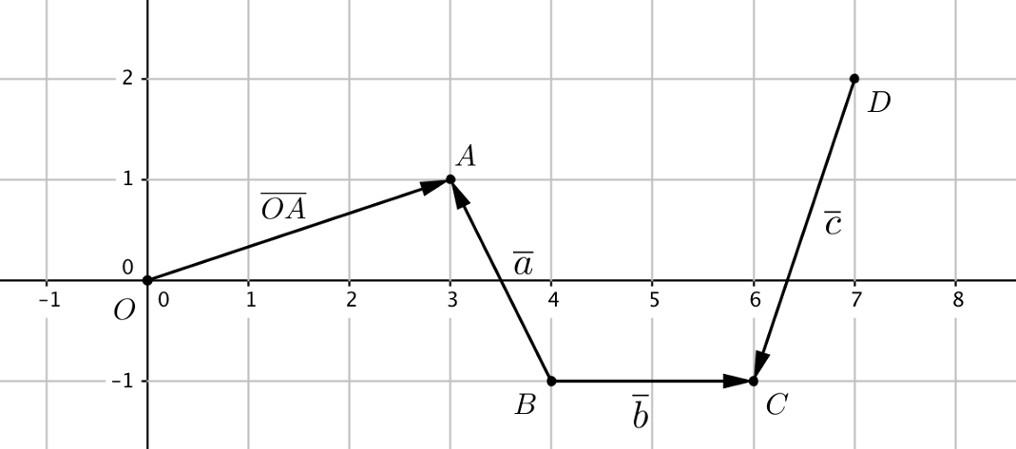
Tarkastele alla olevaa kuvaa. Muodosta kuvan vektoreiden avulla lauseke, jolla kuljetaan
- pisteestä $A$ pisteeseen $C$
- pisteestä $B$ pisteeseen $D$
- origosta eli pisteestä $O$ pisteeseen $B$.
VASTAUS
- $-\va + \vb$ tai yhtä hyvin $\vb - \va$
- $\vb - \vc$
- $\pv{OA} - \va$
Paikkavektori
Tarkastele alla olevaa kuvaa.
- Lausu kuvan vektorit vektoreiden $\vi$ ja $\vj$ avulla.
- Muodosta kuvan vektoreiden avulla lauseke, jolla kuljetaan origosta $O$ pisteeseen $C$.
- Sijoita edellisen kohdan lausekkeeseen a-kohdan vektorit ja sievennä lauseke.
- Katso kuvasta pisteen $C$ koordinaatit. Vertaa tulosta c-kohdan tulokseen.
- Mikä on pisteen $C$ paikkavektori?

VASTAUS
- $\pv{OA} = 3\vi + \vj$, $\quad \va = -\vi + 2\vj$, $\quad\vb = 2\vi$, $\quad\vc = -\vi - 3\vj$
- $\pv{OC} = \pv{OA} - \va + \vb$
- $\pv{OC} = 6\vi - \vj$
- $C = (6,-1)$
- $\pv{OC} = 6\vi - \vj$
Vektoreiden yhdensuuntaisuus
Päättele, ovatko vektorit $\va$ ja $\vb$ yhdensuuntaiset, jos
- $\va=\frac{1}{4}\vi-3\vj$ ja $\vb=\vi-12\vj$
- $\va=-10\vi+\frac{2}{5}\vj$ ja $\vb=\frac{4}{5}\vi+2\vj$?
VASTAUS
- $\vb = 4\va$, joten vektorit $\va$ ja $\vb$ ovat yhdensuuntaiset.
- Vektorit $\va$ ja $\vb$ eivät ole yhdensuuntaiset, sillä ei ole olemassa sellaista lukua $r \neq 0$, jolla $\va = r\vb$. Vertaamalla vektoreita $r\vb=\frac{4}{5}r\vi+2r\vj$ ja $\va=-10\vi+\frac{2}{5}\vj$ havaitaan, että pitäisi olla yhtä aikaa $\frac{4}{5}r = -10$ ja $2r = \frac{2}{5}$, mikä ei ole mahdollista.
Vektorin pituus
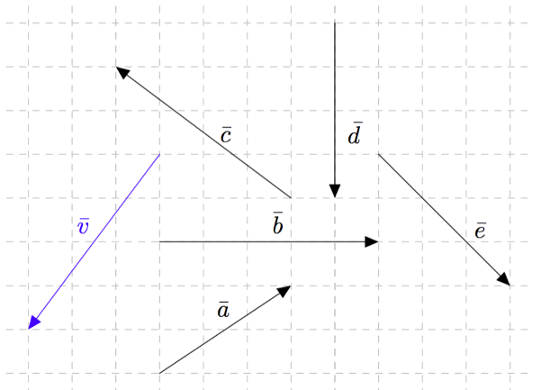
Tarkastele alla olevaa kuvaa. Mitkä kuvan vektoreista ovat yhtä pitkiä kuin vektori $\vv$? Perustele vastauksesi.
VASTAUS
Yhtä pitkiä kuin vektori $\vv$ ovat vektorit $\vb$ ja $\vc$, sillä myös niiden pituus on 5. Vektorin $\va$ pituus on $\sqrt{13}$, vektorin $\bar{d}$ pituus on 4 ja vektorin $\bar{e}$ pituus on $3\sqrt{2}$.
Vektorin pituus
Vektorin $\vv$ pituus on 24.
- Määritä vektoreiden $-6\vv$ ja $\frac{1}{8}\vv$ pituudet.
- Vertaa vektoreiden $-6\vv$ ja $\frac{1}{8}\vv$ suuntaa vektorin $\vv$ suuntaan.
VASTAUS
- $|-6\vv| = 144$ ja $\left|\frac{1}{8}\vv\right| = 3$.
- Vektorit $-6\vv$ ja $\vv$ ovat vastakkaissuuntaiset. Vektorit $\frac{1}{8}\vv$ ja $\vv$ ovat samansuuntaiset.
Yksikkövektori
Muodosta vektorin $\vv=-8\vi+15\vj$ kanssa
- samansuuntainen yksikkövektori
- samansuuntainen vektori, jonka pituus on $4$.
VASTAUS
- $\frac{1}{17}\vv = -\frac{8}{17}\vi + \frac{15}{17}\vj$
- $\frac{4}{17}\vv = -\frac{32}{17}\vi + \frac{60}{17}\vj$
Yksikkövektori
Tiedetään, että vektorin $\vv$ pituus on
- $|\vv| = 8$
- $|\vv| = \sqrt{5}$
- $|\vv| = \frac{1}{3}$.
VASTAUS
- Kysytty yksikkövektori on $\frac{1}{8}\vv$.
- Kysytty yksikkövektori on $\frac{1}{\sqrt{5}}\vv$.
- Kysytty yksikkövektori on $3\vv$.
Vektorin jakaminen komponentteihin
Jaa vektori $\va = 4\vi - 2\vj$ vektoreiden $\vv = 3\vi + \vj$ ja $\vw = -\vi-\vj$ suuntaisiin komponentteihin kuvan avulla päättelemällä. Piirrä komponenttivektorit näkyviin ja ilmaise ne vektorien $\vv$ ja $\vw$ avulla.
VASTAUS
$\va = 3\vv + 5\vw$, joten kysytyt komponenttivektorit ovat $3\vv$ ja $5\vw$.
Pistetulo
Laske vektoreiden $\vv$ ja $\vw$ pistetulo, jos
- $\vv=\frac{1}{2}\vi-3\vj$ ja $\vw=10\vi+7\vj$
- $\vv=9\vi+11\vj$ ja $\vw=\frac{2}{3}\vi-2\vj$
VASTAUS
- $\vv \cdot \vw = -16$
- $\vv \cdot \vw = -16$
Pistetulo
Kolmion kärjet ovat $A=(-4,3)$, $B=(5,2)$ ja $C=(1,-2)$.
- Muodosta vektorit $\pv{AB}$, $\pv{BC}$ ja $\pv{CA}$.
- Osoita pistetulon avulla, että kolmio on suorakulmainen.
VASTAUS
- $\pv{AB} = 9\vi - \vj$, $\quad \pv{BC} = -4\vi - 4\vj$, $\quad\pv{CA} = -5\vi + 5\vj$
- Kärjestä $C$ lähtevien vektoreiden $\pv{CB} = 4\vi + 4\vj$ ja $\pv{CA} = -5\vi + 5\vj$ pistetulo on $\pv{CB} \cdot \pv{CA} = 0$, joten nämä vektorit ovat kohtisuorassa toisiaan vastaan.
Vektoreiden välinen kulma
Kolmion $ABC$ kärjet ovat pisteissä $A=(-7,1)$, $B=(4,9)$ ja $C=(-3,-5)$.
- Laske kolmion kulmien suuruudet asteen tarkkuudella.
- Piirrä kuva kolmiosta $ABC$ ja tarkista kolmioviivoittimella mittaamalla, onko vastauksesi järkevä.
VASTAUS
- Kulma $A$ noin $92^\circ$, kulma $B$ noin $27^\circ$ ja kulma $C$ noin $61^\circ$.
Vektoreiden välinen kulma
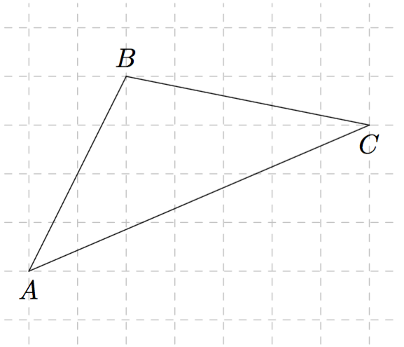
Tarkastele alla olevan kuvan kolmiota. Määritä pistetulon avulla asteen tarkkuudella kulmat
- $\sphericalangle(\pv{AB},\pv{AC})$
- $\sphericalangle(\pv{AB},\pv{CB})$
- $\sphericalangle(\pv{CA},\pv{BC})$.
VASTAUS
- $\sphericalangle(\pv{AB},\pv{AC}) \approx 40^\circ$
- $\sphericalangle(\pv{AB},\pv{CB}) \approx 105^\circ$
- $\sphericalangle(\pv{CA},\pv{BC}) \approx 145^\circ$.
Vektoreiden kohtisuoruus
- Etsi piirroksen avulla vektori, joka on yhtä pitkä kuin vektori $\vv = 2\vi-3\vj$ ja kohtisuorassa sitä vastaan.
- Päättele, mikä vektori on yhtä pitkä kuin vektori $\vw = x\vi+y\vj$ ja kohtisuorassa sitä vastaan.
- Tarkista pistetulon avulla, että b-kohdassa tekemäsi johtopäätös on oikein.
VASTAUS
- Kaksi vaihtoehtoa: $3\vi + 2\vj$ ja $-3\vi - 2\vj$
- Kaksi vaihtoehtoa: $y\vi - x\vj$ ja $-y\vi + x\vj$
TEHTÄVÄSARJA III
Laiva kulkee suoraan tasaisella nopeudella. Eräällä hetkellä laiva on pisteessä $A=(-7,10)$ ja tuntia myöhemmin pisteessä $B=(6,-5)$.
- Määritä vektori, joka kuvaa laivan siirtymää tunnin aikana.
- Missä pisteessä laiva oli kaksi tuntia ennen saapumistaan pisteeseen $A$?
- Missä pisteessä laiva on 40 minuuttia sen jälkeen, kun se jätti pisteen $B$?
VASTAUS
- $\pv{AB} = 13\vi - 15\vj$
- $(-33,40)$
- $\left(\frac{44}{3}, -15\right)$
Tiedetään, että tyynessä säässä kuumailmapallo nousee suoraan ylöspäin nopeudella $3 \frac{\textrm{m}}{\textrm{s}}$. Sääennusteen mukaan lentopäivänä tuuli puhaltaa idästä $4 \frac{\textrm{m}}{\textrm{s}}$ ja kuljettaa palloa kohti länttä nousun aikana.
- Muodosta vektoreiden $\vi$ ja $\vj$ avulla vektori, joka kuvaa kuumailmapallon siirtymää yhden sekunnin aikana.
- Muodosta vektori, joka kuvaa kuumailmapallon siirtymää kahden minuutin aikana.
- Kuinka korkealla kuumailmapallo on kahden minuutin kuluttua lähdöstä?
- Mikä on kuumailmapallon etäisyys lähtöpaikasta kahden minuutin kuluttua?
VASTAUS
- Esimerkiksi $-4\vi + 3\vj$
- Esimerkiksi $-480\vi + 360\vj$
- Noin 360 metrin korkeudella.
- Noin 600 metriä.
Suunnikkaan kolme kärkipistettä ovat $(-1,2), (5,2)$ ja $(1,5)$. Määritä suunnikkaan neljäs kärkipiste
- kuvan avulla
- vektoreiden avulla.
VASTAUS
Neljäs kärkipiste voi olla $(-5,5)$ tai $(3,-1)$ tai $(7,5)$.
Tutki vektoreita $\va=2\vi+3\vj$, $\vb=-3\vi+\vj$ ja $\vc=\vi-4\vj$.
- Piirrä vektori $\va +\vb +\vc$ koordinaatistoon vektoreiden $\va$, $\vb$ ja $\vc$ avulla.
- Selitä omin sanoin, mitä huomaat.
- Miten voit ilmaista vektorin $\vc$ vektoreiden $\va$ ja $\vb$ avulla?
VASTAUS
- $\vc = -\va - \vb$
Tarkastele pisteitä $A=(2{,}-5)$ ja $B=(5{,}1)$.
- Piirrä pisteet $A$ ja $B$ yhdistävä jana koordinaatistoon.
- Sijoita piste $P$ janalle silmämääräisesti siten, että se jakaa janan $AB$ suhteessa $2:3$.
- Lausu vektori $\pv{AP}$ vektorin $\pv{AB}$ avulla.
- Määritä pisteen $P$ koordinaatit.
VASTAUS
- $\pv{AP} = \frac{2}{5}\pv{AB}$
- $P = \left(\frac{16}{5}, -\frac{13}{5}\right) = (3{,}2; -2{,}6)$
Tarkastele alla olevaa kuvaa.
- Ilmoita vektorit $\vv$ ja $\vw$ vektoreiden $\vi$ ja $\vj$ avulla.
- Laske vektoreiden $\vv$ ja $\vw$ pituudet.
- Muodosta vektori $3\vv-4\vw$ ja laske sen pituus.
VASTAUS
- $\vv = -5\vi + 2\vj\ $ ja $\ \vw = -4\vi-4\vj$
- $|\vv| = \sqrt{29} \ $ ja $\ |\vw| = \sqrt{32} = 4\sqrt{2}$
- $3\vv - 4\vw = \vi + 22\vj\ $ ja $\ |3\vv - 4\vw| = \sqrt{485}$
Tutki, onko olemassa sellainen reaaliluku $r$, että vektorit $\vv=(2+3r)\vi-4\vj$ ja $\vw=5\vi+(r-5)\vj$ ovat
- yhdensuuntaiset
- samat.
Ovatko vektorit $\vv$ ja $\vw$ a-kohdan tapauksessa samansuuntaiset vai vastakkaissuuntaiset? Voit ratkaista ratkaisussa muodostuvat yhtälöparit laskimella.
VASTAUS
- Kyllä, $r = \frac{10}{3}$.
- Kyllä, $r = 1$.
Kohdassa (a) vektorit ovat samansuuntaiset.
Määritä vektoreiden $\va=2\vi+5\vj$ ja $\vb=\vi-2\vj$ summavektori ja summavektorin suuntainen yksikkövektori. [Pitkä K09/3a]
VASTAUS
$\va + \vb = 3\vi + 3\vj$ ja samansuuntainen yksikkövektori on $\dfrac{1}{\sqrt{2}}\vi + \dfrac{1}{\sqrt{2}}\vj$.
Selvitä, mihin pisteeseen päädyt, jos siirryt
- pisteestä $A=(7,3)$ kymmenen pituusyksikköä vektorin $\vv=3\vi-4\vj$ suuntaan
- pisteestä $B=(4,-8)$ viisi pituusyksikköä vektorin $\vv=-12\vi+9\vj$ suuntaan.
VASTAUS
- Pisteeseen $(13,-5)$.
- Pisteeseen $(0,-5)$.
Vektorien $\pv{AB}$ ja $\pv{CD}$ päätepisteet ovat $A=(3,1)$, $B=(7,3)$, $(C=1,4)$ ja $D=(-3,-2)$. Laske vektorien välisen kulman suuruus $0{,}1$ asteen tarkkuudella. Piirrä kuvio. [Pitkä S05/3]
VASTAUS
Noin $150{,}3^\circ$.
Tutki, onko kolmio suorakulmainen, jos sen eräästä kärjestä alkavat sivuvektorit ovat
- $\va=3\vi+\vj$ ja $\vb=2\vi+6\vj$
- $\va=-4\vi-3\vj$ ja $\vb=-2\vi-4\vj$.
VASTAUS
- Kolmio ei ole suorakulmainen. Kärkipisteet voivat olla esimerkiksi $O=(0,0)$, $A=(3,1)$ ja $B=(2,6)$. Kulmiksi saadaan noin $53^\circ$, noin $97^\circ$ ja noin $30^\circ$.
- Kolmio on suorakulmainen. Kärkipisteet voivat olla esimerkiksi $O=(0,0)$, $A=(-4,-3)$ ja $B=(-2,-4)$. Kulma $\sphericalangle(\pv{BA}, \pv{BO}) = 90^\circ$.
Kolmiossa $ABC$ on $\pv{AB}=2{,}2\vi+7{,}3\vj$ ja $\pv{AC}=5{,}9\vi-2{,}1\vj$.
- Määritä kolmanteen sivuun liittyvä vektori $\pv{BC}$.
- Osoita, että $BC$ on kolmion pisin sivu.
- Määritä kulman $BAC$ suuruus pistetulon avulla 0,1 asteen tarkkuudella.
VASTAUS
- $\pv{BC} = 3{,}7\vi - 9{,}4\vj$
- $|\pv{AB}| = \sqrt{58{,}13}$, $|\pv{AC}| = \sqrt{39{,}22}$ ja $|\pv{BC}| = \sqrt{102{,}05}$, joten sivu $BC$ on pisin (sen pituuden lausekkeessa juurrettava on suurin).
- Noin $92{,}8^\circ$.
Olkoon $\pv{OA}=7\vi+9\vj$ tason vektori. Määritä kaikki sellaiset vektorit $\pv{OB}$, että kulma OAB on suora ja vektorin $\pv{AB}$ pituus on puolet vektorin $\pv{OA}$ pituudesta. [Pitkä K2005/4]
VASTAUS
Kaksi mahdollisuutta: $\frac{23}{2}\vi + \frac{11}{2}\vj$ tai $\frac{5}{2}\vi + \frac{25}{2}\vj$.
Origosta alkavan vektorin $\va=2\vi+7\vj$ päätepisteestä $P$ alkava ja $x$-akselin pisteeseen $Q$ päättyvä vektori $\vb$ on kohtisuorassa vektoria $\va$ vastaan. Määritä pisteet $P$ ja $Q$ sekä vektori $\vb$. [Lyhyt K1989/6a]
VASTAUS
$P = (2,7)$, $\ Q = \left(\frac{53}{2}, 0\right)\ $ ja $\ \vb = \frac{49}{2}\vi - 7\vj$
Lentäjä ohjaa lentokonetta länteen. Tyynessä säässä lentokone liikkuisi suoraan länttä kohti $210~\frac{\textrm{km}}{\textrm{h}}$, mutta tuuli puhaltaa pohjoisesta $25~\frac{\textrm{m}}{\textrm{s}}$ ja kuljettaa konetta etelän suuntaan.
- Mihin suuntaan lentokone todellisuudessa lentää?
- Mikä on lentokoneen vauhti maan suhteen?
VASTAUS
- Noin 23,2 astetta lännestä etelän suuntaan (kompassisuuntaan $246{,}8^\circ$).
- Noin 228 km/h.
Vedät pulkkaa voimalla $\bar{F} = x\vi + y\vj$, jonka suuruus on $|\bar{F}| = 150~\textrm{N}$.
- Mikä on vektorin $\vj$ suuntaisen komponentin suuruus, jos vektorin $\vi$ suuntaisen komponentin suuruus on 90 N?
- Jos vektoreiden $\vi$ ja $\vj$ suuntaiset komponentit ovat yhtä suuret, kuinka suuret ne ovat?
VASTAUS
- 120 N
- Noin 106 N.
Voiman $\bar{F} = x\vi + y\vj$ suuruus on $|\bar{F}| = 84~\textrm{N}$. Mikä on vektorin $\vi$ suuntaisen komponentin suuruus, jos vektorin $\vj$ suuntaisen komponentin suuruus on 60,2 N? Havainnollista ratkaisuasi piirtämällä tilanteesta mallikuva.
VASTAUS
Noin 58,6 N.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitestit opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla. Linkit luvun itsearviointitesteihin ovat tässä: ensimmäinen testi ja toinen testi.

