Diskreetti kahden muuttujan jakauma
Luvun tavoitteet
Tämän luvun tavoitteena on, että pystyt xxxx. Osaat
- xxxxx
- xxxxx
- xxxxx.
Korrelaatiokerroin
Tähän asti olemme tarkastelleet esimerkkejä, joissa havaintoyksikköön liitty yksi havaintoarvo. Usein kuitenkin havaintoyksikköön liitty useita havaintoarvoja. Esimerkiksi lapsiperhe-esimerkissä jokaiselta lapsiperheeltä voisi lasten lukumäärän lisäksi olla tiedot vaikkapa asuinpaikkakunnasta ja perheen tulotasosta. Kaikki edellä esitetyt tarkastelut toimivat yksittäisille havaintoarvoille. Seuraavaksi tarkastelemme, miten kahta eri havaintoarvoa voi vertailla keskenään.
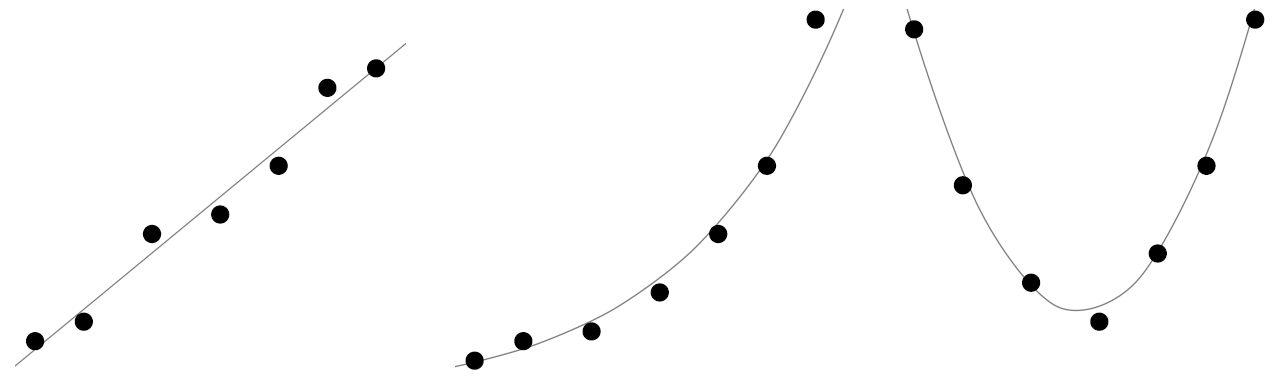
Kun halutaan vertailla kahta eri havaintoarvoa, niin usein on hyödyllistä piirtää tilanteesta kuva. Kutakin havaintoyksikköä kohden saamme yhden parin havaintoarvoja. Tässä parissa ensimmäinen havaintoarvo tulkitaan $x$-akselin arvoksi ja toinen $y$-akselin arvoksi. Kuvassa~\ref{fig:erilaisia_korrelaatioita} on havainnollistettu kolmea erilaista tapausta. Kuvasta huomataan, että vasemmanpuoleisten pisteiden kautta voidaan lähes piirtää suora. Vastaavasti keskimmäisessä kuvassa pisteiden kautta voidaan lähes piirtää eksponentiaalinen käyrä ja oikealla paraabeli. Jos kahden havaintoarvon muodostamat pisteet noudattavat jotain käyrää, niin puhutaan havaintoarvojen korrelaatiosta. Tällä kurssilla tarkastelemme ainoastaan lineaarista korrelaatiota (eli Pearsonin korrelaatiota).
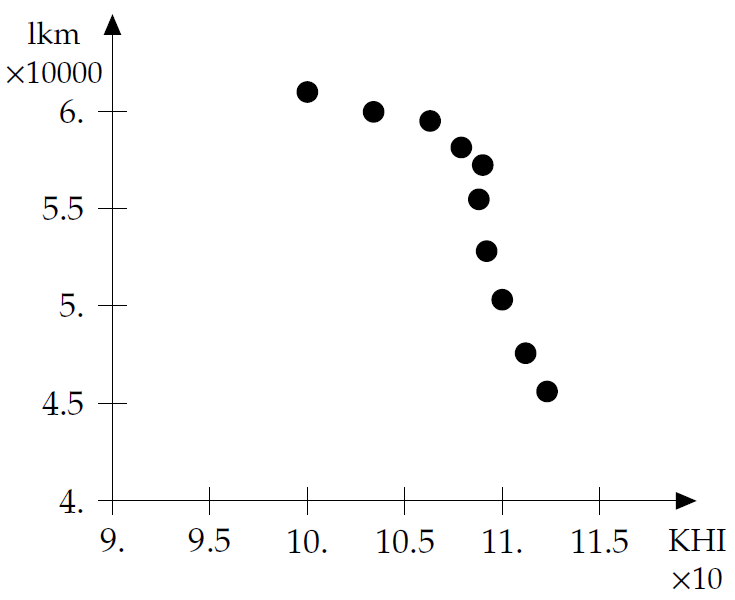
Alla olevassa taulukossa on esitetty syntyneiden lasten lukumäärä ja kuluttajahintaindeksi (KHI) Suomessa vuosina 2010--2019. Tiedot ovat Tilastokeskuksen sivuilta 1ja 2 (luettu 4.1.2020). Vuosi on havaintoyksikkö ja siihen liittyy kaksi havaintoarvoa. Kuluttajahintaindeksi on valittu $x$-akselille ja skaalattu jakamalla luku 10:llä, syntyneiden lasten lukumäärä on $y$-akselilla ja se on skaalattu jakamalla lukumäärä 10000:lla. Huomaa, että havaintoarvot olisi voitu valita akseleille myös toisin päin. Saamme pisteet (10,0; 6,0980), (10,34; 5,9961), ..., (11,12; 4,7577), (11,23; 4,5613), jotka on piirretty kuvaan:
| Vuosi | Syntyneet | KHI |
|---|---|---|
| 2010 | 60980 | 100,0 |
| 2011 | 59961 | 103,4 |
| 2012 | 59493 | 106,3 |
| 2013 | 58134 | 107,9 |
| 2014 | 57232 | 109,0 |
| 2015 | 55472 | 108,8 |
| 2016 | 52814 | 109,2 |
| 2017 | 50321 | 110,0 |
| 2018 | 47577 | 111,2 |
| 2019 | 45613 | & 112,3 |
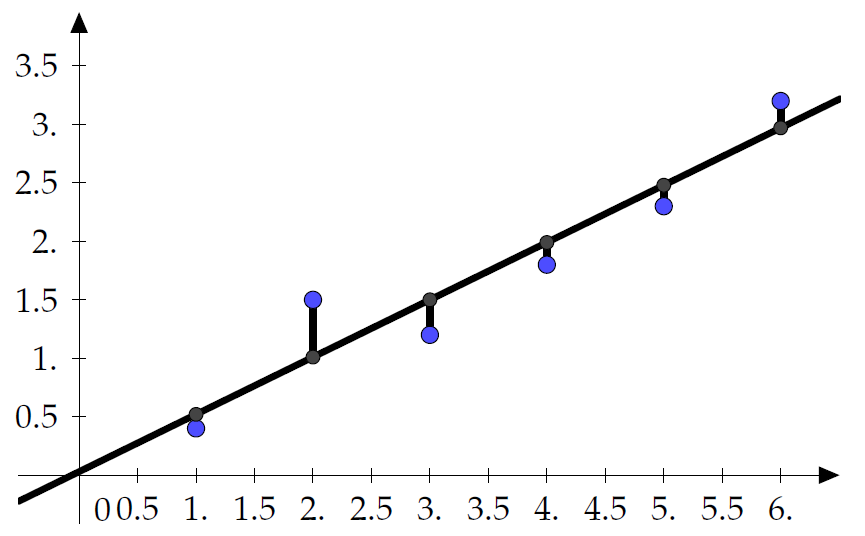
Seuraavaksi yritämme sovittaa havaintopareihin suoran, joka parhaalla mahdollisella tavalla kuvaa muuttujien $x$ ja $y$ välistä yhteyttä. Olkoon suoran yhtälö $y= bx +a$. Pyrimme määrittämään vakiot $a$ ja $b$ siten, että havaintopisteiden $y$-suunnassa laskettujen pystysuorien poikkeamien summa on mahdollisimman pieni. Pisteessä $(x_i, y_i)$ $y$-suuntaan laskettu pystysuora poikkeama suorasta $y= bx +a$ on $|y_i- bx_i -a|$ ja tämän neliö on $(y_i - bx_i -a)^2$. Laskemme nämä kaikki pystysuorien poikkemien neliöt yhteen ja saamme $$ \sum_{i=1}^n (y_i - bx_i -a)^2. $$ Haluamme löytää sellaiset kertoimet $a$ ja $b$, että tämä summa on mahdollisimman pieni.
Tutkimustehtävä GeoGebralla
Piirrä pisteet $(1{,}0; 0{,}4), (2{,}0; 1{,}5), (3{,}0; 1{,}2), (4{,0}; 1{,}8), (5{,}0; 2{,}3)$ ja $(6{,}0; 3{,}2)$ GeoGebralla. Tee liu'ut $a \in [-3, 3]$ ja $b\in [-3, 3]$. Piirrä suora $y= bx + a$. Laske ensin kunkin pisteen $y$-suuntainen etäisyys suorasta ja sitten etäisyyksien summa. Tutki liukujen $a$ ja $b$ avulla, milloin summa on pienin. Vertaa tulostasi yllä olevaan kuvaan.
VASTAUS
xxxxxxx
Voidaan todistaa, että $y$-suuntaisten etäisyyksien summa saa pienimmän arvonsa, kun valitaan $$ \begin{equation} b=\frac{n\sum\limits_{i=1}^n x_iy_i -\sum\limits_{i=1}^n x_i \sum\limits_{i=1}^n y_i}{n\sum\limits_{i=1}^n x_i^2 -\bigg(\sum\limits_{i=1}^n x_i\bigg)^2}\quad \text{ja}\quad a=\frac{\sum\limits_{i=1}^n y_i-b\sum\limits_{i=1}^n x_i}{n}. \end{equation} $$ Ohitamme tämän todistuksen. Kyseistä metodia kutsutaan pienimmän neliösumman menetelmäksi.
MÄÄRITELMÄ: REGRESSIOSUORA
Jos lukuparit $(x_i,y_i)$, $i=1,\ldots,n$, ovat tilastollisten muuttujien $x$ ja $y$ havaintoarvoja, niin suoraa $y=bx+a$, missä $b$ ja $a$ ovat $$ \begin{equation} b=\frac{n\sum\limits_{i=1}^n x_iy_i -\sum\limits_{i=1}^n x_i \sum\limits_{i=1}^n y_i}{n\sum\limits_{i=1}^n x_i^2 -\bigg(\sum\limits_{i=1}^n x_i\bigg)^2}\quad \text{ja}\quad a=\frac{\sum\limits_{i=1}^n y_i-b\sum\limits_{i=1}^n x_i}{n}. \end{equation} $$ kutsutaan regressiosuoraksi.
Regressiosuoran kerroin $b$ voi olla nolla, positiivinen tai negatiivinen. Jos $b$ on positiivinen, niin silloin suora on kasvava. Tällöin muuttujan $x$ kasvaessa myös muuttuja $y$ kasvaa, ja toisinpäin. Sanomme tällöin, että muuttujilla on positiivinen korrelaatio. Jos $b$ on negatiivinen, niin silloin suora on vähenevä. Tällöin muuttujan $x$ kasvaessa muuttuja $y$ vähenee ja muuttujan $y$ kasvaessa muuuttuja $x$ vähenee. Sanomme tällöin, että muuttujilla on negatiivinen korrelaatio.
Korrelaation voimakkuutta mitataan korrelaatiokertoimella.
MÄÄRITELMÄ: KORRELAATIOKERROIN
Tilastollisten muuttujien $x$ ja $y$ korrelaatiokerroin on $$ r = \frac{\sum_{i=1}^n (x_i - \bar x)(y_i- \bar y)}{\sqrt{\sum_{i=1}^n(x_i- \bar x)^2 \sum_{i=1}^m (y_i - \bar y)^2}}, $$ missä $\bar x$ ja $\bar y$ ovat muuttujien $x_1, \ldots, x_n$ ja $y_1, \ldots, y_n$ keskiarvot.
Korrelaatiokerroin on määritelty, jos jokin havaintoarvoista $x_i$ eroaa keskiarvosta $\bar x$ ja jokin havaintoarvoista $y_i$ eroaa keskiarvosta $\bar y$. Huomaa, että $\bar x = \frac1n \sum_{i=1}^n x_i$ ja $\bar y = \frac1n \sum_{i=1}^n y_i$. Käytännössä regressiosuora ja korrelaatiokerroin lasketaan aina ohjelmistolla. Korrelaatiokertoimelle saadaan seuraavat rajat: $$ -1\leqslant r \leqslant 1. $$ Tulos ei ole todistettavissa lukiotiedoin.
Lisätieto: Korrelaatiokerroin voidaan esittää myös muodossa $$ r=\frac{n\sum\limits_{i=1}^n x_iy_i -\sum\limits_{i=1}^n x_i \sum\limits_{i=1}^n y_i}{\sqrt{\left(n\sum\limits_{i=1}^n x_i^2 -\bigg(\sum\limits_{i=1}^n x_i\bigg)^2\right) \left(n\sum\limits_{i=1}^n y_i^2 -\bigg(\sum\limits_{i=1}^n y_i\bigg)^2\right)}}. $$ Korrelaatiokertoimen neliötä $r^2$ sanotaan selitysasteeksi.
Tutkimustehtävä GeoGebralla
Laske (ohjelmistolla) kuluttajahintaindeksin ja lasten lukumäärän (kts. aiemmasta taulukosta) välinen regressiosuora ja korrelaatiokerroin, kun kuluttajahintaindeksi on $x$-akselilla. Vaihda lasten lukumäärä $x$-akselille ja laske regressiosuora ja korrelaatiokerroin. Mitä havaitset?
VASTAUS
xxxxxxx
Korrelaatiokertoimen $r$ merkki on sama kuin regressiosuoran $y= bx +a$ kulmakertoimen $b$ merkki. Näin ollen korrelaatiokertoimen merkki kertoo, onko kyseessä positiivinen vai negatiivinen korrelaatio.
Korrelaatiokerroin $r$ kuvaa muuttujien $x$ ja $y$ lineaarisen riippuvuuden voimakkuutta. On syytä huomata, että tämä riippuvuus on tilastollista riippuvuutta. Mitään syy-yhteyttä muuttujien välillä ei välttämättä ole. Mitä lähempänä korrelaatiokertoimen itseisarvo $|r|$ on lukua $1$, sitä voimakkaampaa muuttujien $x$ ja $y$ riippuvuus on.
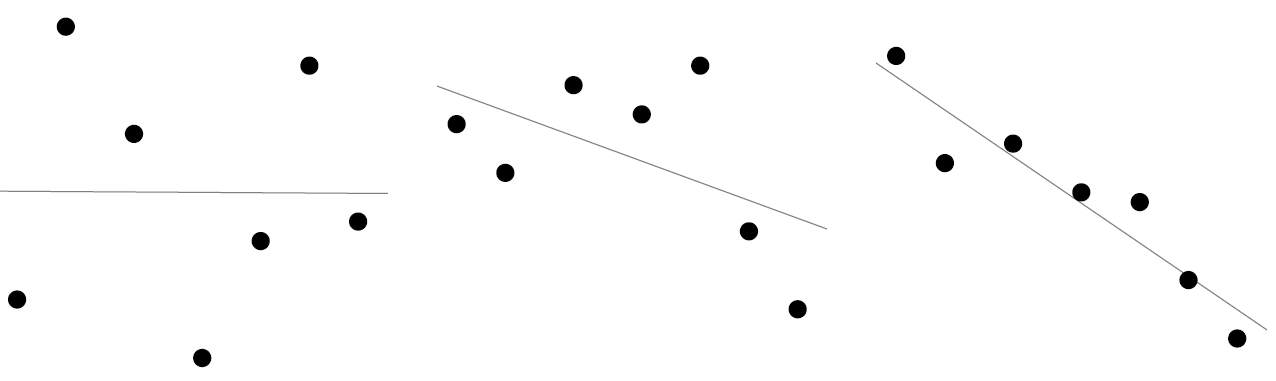
Lisätieto: Jos $|r|=1$, niin kaikki havaintoarvopisteet ovat samalla suoralla.
Tutkimustehtävä GeoGebralla
Alla olevaan taulukkoon on koottu vapaa-ajan kalastajien lukumäärät (1000 henkilöä) ja vapaa-ajan kalastajien kuhasaaliiden koot (1000 kg) kahden vuoden välein vuosilta 2004--2018. Luvut ovat Tilastokeskuksen sivuilta (luettu 13.10.2020). Muodostetaan aineistosta havaintoparit $(1858, 2265), \ldots, (1461, 3348)$ ja syötetään havaintoparit ohjelmistoon. Saamme regressiosuoraksi $y= -2{,}92x + 7830{,}81$, missä $x$ on vapaa-ajan kalastajien lukumäärä (1000 kpl) ja $y$ on kuhasaalis (1000 kg). Korrelaatiokertoimeksi $r$ saamme $-0{,}87$, eli kalastajien lukumäärällä ja kuhasaaliilla on negatiivinen korrelaatio.
| Vuosi | Kalastajat (1000 hlöä) | Kuhasaalis (1000 kg) |
|---|---|---|
| 2004 | 1858 | 2265 |
| 2006 | 1844 | 2790 |
| 2008 | 1780 | 2368 |
| 2010 | 1676 | 2865 |
| 2012 | 3246 | 109,0 |
| 2014 | 3348 | 108,8 |
| 2016 | 3892 | 109,2 |
| 2018 | 1461 | 3378 |
- Tee GeoGebralla itse vastaava analyysi.
- Onko suureilla syy-yhteyttä?
VASTAUS
-

- Tilastollisesta yhteydestä huolimatta suureilla tuskin on syy-yhteyttä, koska vapaa-ajan kalastajien määrän vähenemisen luulisi vähentävän myös kuhasaaliita.
Korrelaatiota
Keksi kahden muuttujan esimerkkejä, joissa on positiivista tai negatiivista korrelaatiota, mutta ei syy-yhteyttä.
VASTAUS
TEHTÄVÄSARJA II
Tehtävä
Selvitä funktion $f$ määrittelyjoukko ja nollakohdat, jos
- $f(x) = x - 3\sqrt{x-1} + 1$
- $f(x) = \sqrt{x} + x - 1$
Vastaus
- Funktio on määritelty, jos ja vain jos $x \geq 1$.
Funktiolla on nollakohdat $x_1 = 2$ ja $x_2 = 5$. - Funktio on määritelty, jos ja vain jos $x \geq 0$.
Funktiolla on nollakohta $$ x = \frac{3 - \sqrt{5}}{2}. $$
TEHTÄVÄSARJA III
- Sievennä lauseke $$\sqrt{a\sqrt{a\sqrt{a^2}}},$$ kun $a \geq 0$.
- Luku on yhtä suuri kuin puolet sen neliöjuuresta. Määritä kaikki tällaiset luvut.
[Pitkä S2016/2a & S2014/2b]
Vastaus
- \begin{align*} \sqrt{a\sqrt{a\sqrt{a^2}}} &= \sqrt{a\sqrt{a^2}} \\ &= \sqrt{a^2} \\ &= a \end{align*}
- Kysytyt luvut ovat $0$ ja $\dfrac{1}{4}$.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

