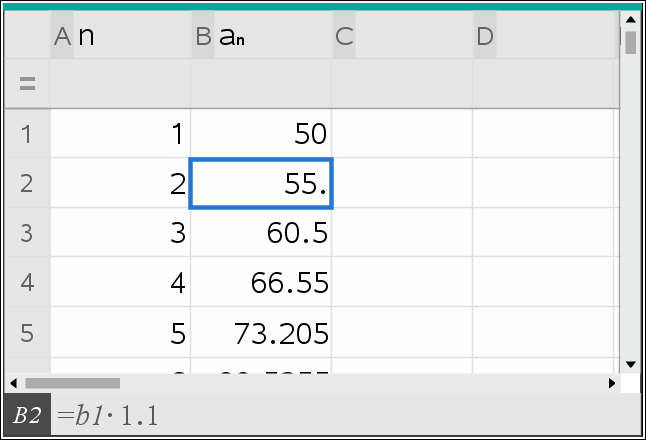
Lukujono tarkoittaa nimensä mukaisesti lukujen muodostamaa, yleensä päättymätöntä jonoa. Esimerkiksi 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 9, $\ldots$ on eräs lukujono. Tästä jonosta on vaikea sanoa, miten se jatkuu. Yleensä lukujonoon liittyy jokin sääntö, jonka avulla voidaan päätellä, mitkä ovat jonon seuraavat luvut.
Lukujonon lukuja sanotaan jonon termeiksi tai jäseniksi. Voidaan esimerkiksi sanoa, että edellä mainitun lukujonon ensimmäinen jäsen on 3 tai että sen kuudes termi on 9.
Joskus lukujonosta on helpompi puhua, jos sille annetaan nimi. Voidaan esimerkiksi puhua lukujonosta $(a_n)$ tai lukujonosta $(b_n)$ tai lukujonosta $(x_n)$. Tässä merkinnässä sulut kertovat sen, että puhutaan koko lukujonosta eikä yksittäisestä jonon jäsenestä.
Kun lukujono on nimetty esimerkiksi jonoksi $(a_n)$, tarkoittaa merkintä $a_1$ sen ensimmäistä jäsentä, $a_2$ sen toista jäsentä, $a_3$ sen kolmatta jäsentä ja niin edelleen. Jos halutaan esimerkiksi puhua jonon $(a_n)$ sadannesta jäsenestä, voidaan käyttää merkintää $a_{100}$. Alaindeksi siis kertoo, kuinka mones jonon jäsen on kysymyksessä.
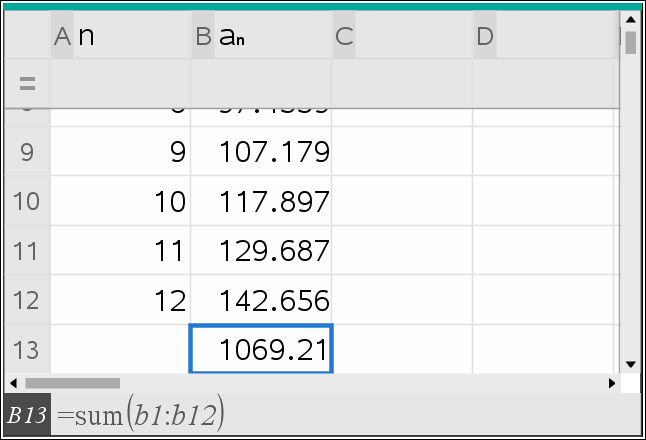
Edellisissä tehtävissä tutkittiin, onko annettu luku tietyn lukujonon jäsen. Esimerkiksi voidaan kysyä, onko luku $1280$ edellisessä tehtävässä tarkastellun lukujonon $(b_n)$ jäsen. Toisin sanottuna, onko olemassa sellainen positiivinen kokonaisluku $n$, että $b_n = 1280$. Jos tällainen luku $n$ on olemassa, se kertoo, kuinka mones jonon jäsen luku $1280$ on.
Kysymys, onko luku $1280$ lukujonon $(b_n)$ jäsen, johtaa siis yhtälöön $b_n = 1280$. Kysymykseen saadaan vastaus, kun tutkitaan, onko olemassa sellainen $n$, jolla tämä yhtälö toteutuu. Jos tällainen $n$ on olemassa, se on yhtälön $b_n = 1280$ ratkaisu.
Koska tiedetään, että lukujonon $(b_n)$ yleinen jäsen on $b_n=3n+5$, voidaan yhtälö $$b_n = 1280$$ kirjoittaa muodossa $$3n + 5 = 1280.$$ Tässä yhtälössä on yksi tuntematon, joka on tässä tapauksessa luku $n$. Kun yhtälö ratkaistaan, etsitään kaikki sellaiset luvut $n$, joilla yhtälö toteutuu eli joilla sen vasen ja oikea puoli ovat yhtä suuret.
Kun yhtälö ratkaistaan, voidaan sitä muokata monin eri tavoin. Tärkeää kuitenkin on, että yhtälön kummallekin puolelle tehdään aina sama asia. Tällä tavalla yhtälön oikea ja vasen puoli säilyvät yhtä suurina. Esimerkiksi yhtälön $$3n + 5 = 1280$$ molemmilta puolilta voidaan vähentää luku $5$, jolloin vasemmalle puolelle jää pelkkä $3n$ ja oikealle puolelle jää $1275$. Saadaan siis uusi yhtälö $$3n = 1275.$$ Yhtälön vasemmalla puolella olleesta yhteenlaskettavasta $5$ päästiin siis eroon käyttämällä päinvastaista laskutoimitusta eli vähennyslaskua.
Yhtälön vasemmalla puolella on kuitenkin vielä ylimääräinen luku $3$. Se on tuntemattoman $n$ kerroin, joten siitä päästään eroon jakolaskun avulla. Jaetaan yhtälön molemmat puolet luvulla $3$, jolloin saadaan uusi yhtälö $$\frac{3n}{3} = \frac{1275}{3}.$$ Tämän yhtälön vasen puoli on sama kuin pelkkä $n$, koska kolmosella kertominen ja jakaminen kumoavat toisensa. Esimerkiksi laskimen avulla nähdään, että oikea puoli on sama kuin $425$. Siis $$n = 425.$$
Tähän mennessä tehdyt laskut osoittavat, että yhtälöllä $3n + 5 = 1280$ ei voi olla mitään muita ratkaisuja kuin $n = 425$. Vielä pitää kuitenkin tarkistaa, että luku $n = 425$ todella on tämän yhtälön ratkaisu. Jos yhtälön vasemmalle puolelle sijoitetaan $n = 425$, saadaan $$ \begin{align*} 3n + 5 &= 3\cdot 425 + 5 \\ &= 1275 + 5 \\ &= 1280. \end{align*} $$ Huomataan, että vasemmasta puolesta saadaan tuloksena alkuperäisen yhtälön oikea puoli. Yhtälö siis toteutuu.
Näin on saatu selville, että yhtälöllä $3n + 5 = 1280$ eli yhtälöllä $b_n = 1280$ on yksi ratkaisu, joka on $n = 425$. Siis $b_{425} = 1280$. Tämän perusteella voidaan sanoa, että luku 1280 on lukujonon $(b_n)$ jäsen, tarkemmin sanottuna 425. jäsen.
Joskus lukujonoon liittyvä sääntö voidaan esittää niin, että sen avulla voidaan laskea jonon seuraava jäsen, jos tiedetään, mitä jonon edelliset jäsenet ovat. Tarkastellaan esimerkiksi tilannetta, jossa tiedetään, että lukujonon $(a_n)$ ensimmäinen jäsen on $a_1 = 1$ ja että seuraava jäsen saadaan aina edellisestä jäsenestä lisäämällä siihen kaksi. Tämä sääntö voidaan kirjoittaa muodossa $a_1 = 1$ ja $$ a_n = a_{n-1} + 2$$ kaikilla luonnollisilla luvuilla $n\geq 2$ eli luonnollisilla luvuilla $n$, jotka ovat suurempia tai yhtä suuria kuin luku $2$. Tällaisessa tilanteessa sanotaan, että lukujono on määritelty rekursiivisesti. Rekursioyhtälön avulla voidaan laskea, että $$ \begin{align*} a_2 &= a_1 + 2 = 1 + 2 = {\textcolor{blue}{3}}\\ a_3 &= a_2 + 2 = {\textcolor{blue}{3}} + 2 = {\textcolor{green}{5}} \\ a_4 &= a_3 + 2 = {\textcolor{green}{5}} + 2 = {\textcolor{red}{7}} \\ a_5 &= a_4 + 2 = {\textcolor{red}{7}} + 2 = {\textcolor{magenta}{9}} \\ a_6 &= a_5 + 2 = {\textcolor{magenta}{9}} + 2 = 11 \\ \end{align*} $$
Lukujonosta $(a_n)$ tiedetään, että $a_1 = 3$ ja $a_n = a_{n-1} + 4$ kaikilla $n \geq 2$. Määritä $a_2$, $a_3$, $a_4$, $a_5$ ja $a_6$.
$a_2 = 7$, $a_3 = 11$, $a_4 = 15$, $a_5 = 19$ ja $a_6 = 23$.
Rekursiivisen jonon ensimmäinen jäsen on 3 ja seuraavat saadaan kertomalla edellinen jäsen luvulla 2.
- Määritä $a_2$, $a_3$ ja $a_4$.
- Selitä, miten saisit määritettyä jäsenen $a_{20}$.
- Kirjoita rekursiokaava jonon yleiselle jäsenelle $a_n$.
- $a_2 = 6$, $a_3 = 12$ ja $a_4 = 24$.
- Jatkamalla kahdella kertomista kunnes päästään jäseneen $a_{20}$.
- $a_n = 2a_{n-1}$ kaikilla $n \geq 2$.


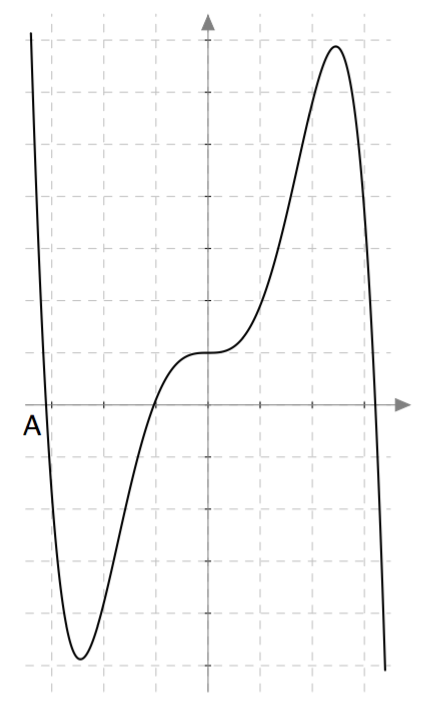
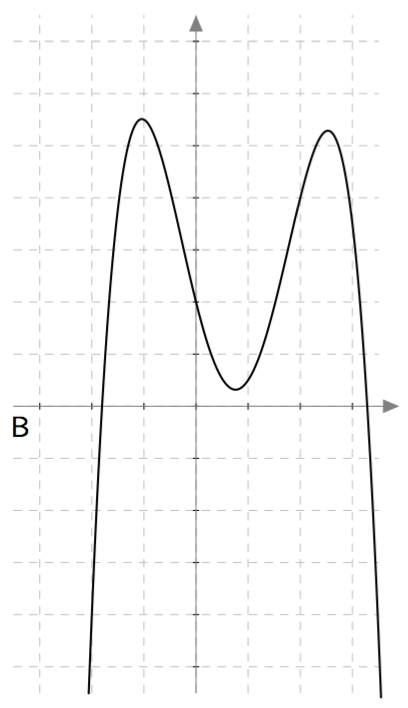
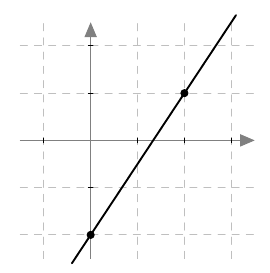
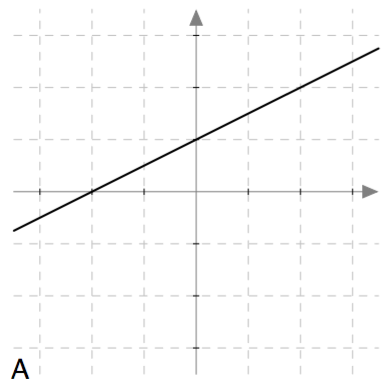
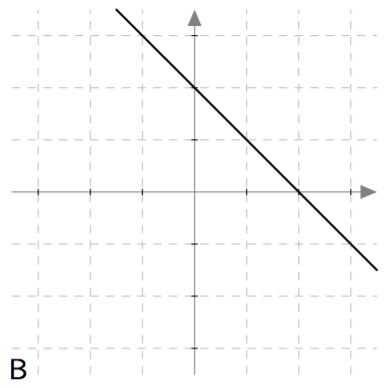
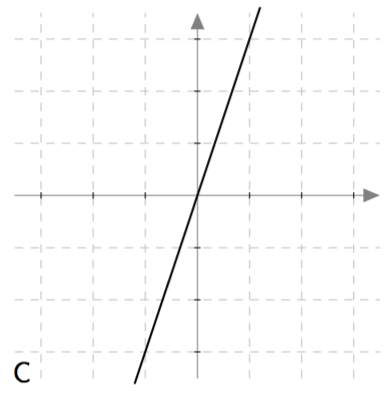
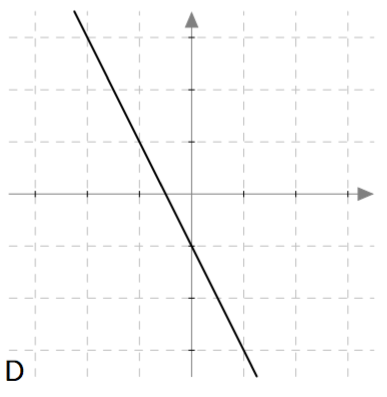
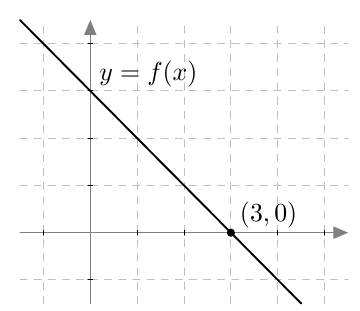
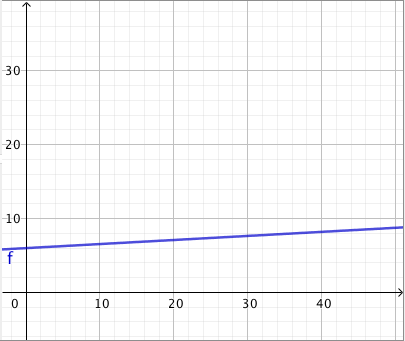
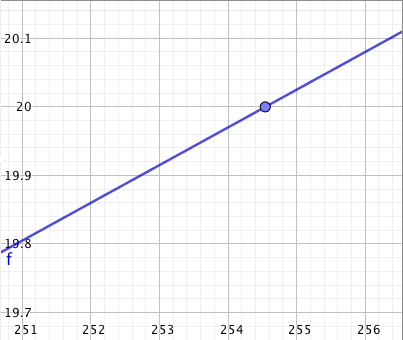
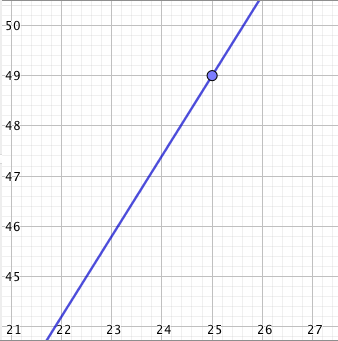
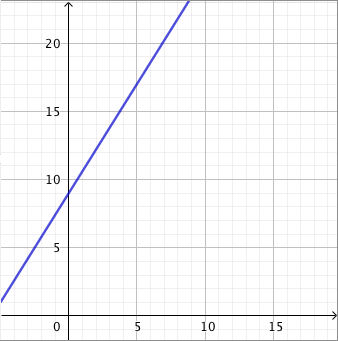
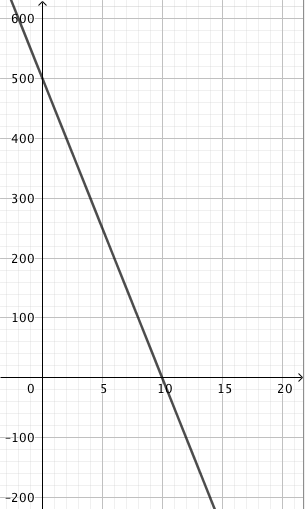
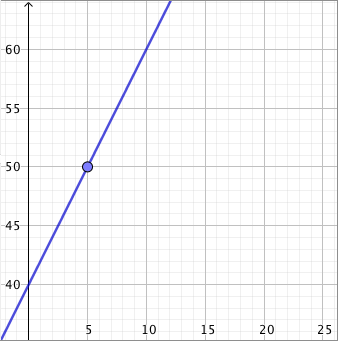
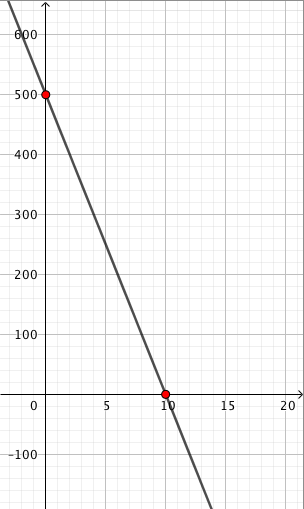
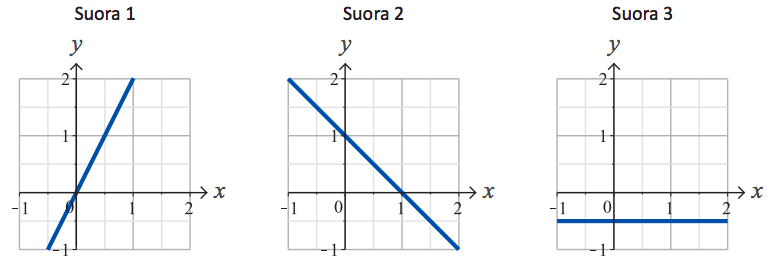
 Päättele kuvaajan avulla vastaukset seuraaviin kysymyksiin:
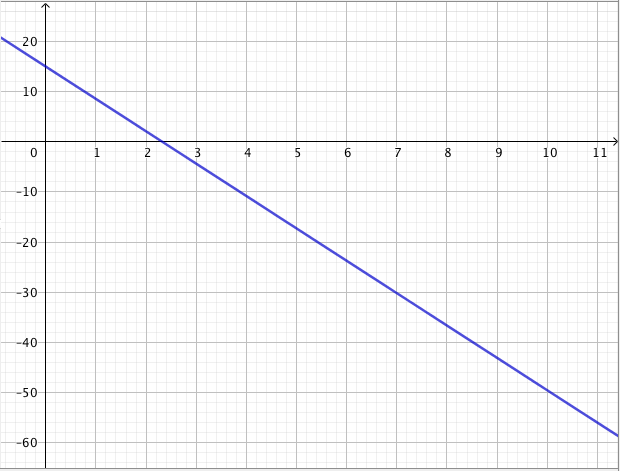
Päättele kuvaajan avulla vastaukset seuraaviin kysymyksiin: