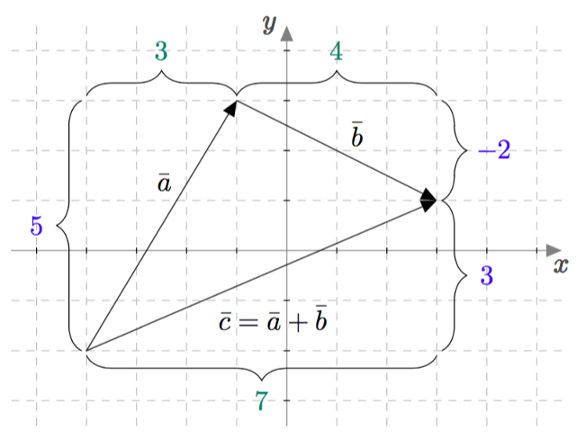
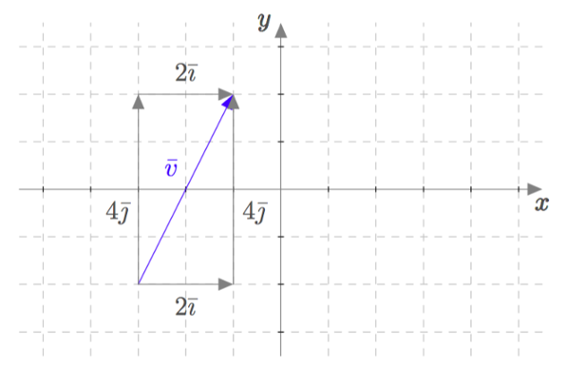
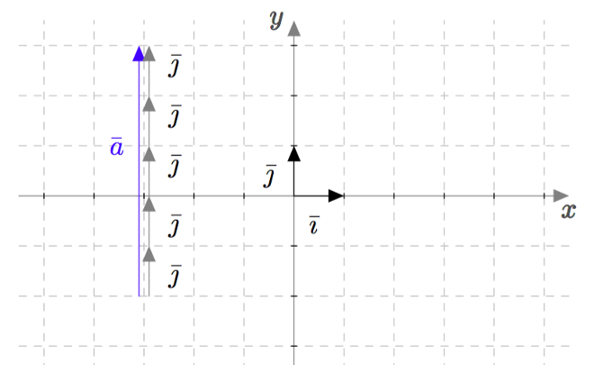
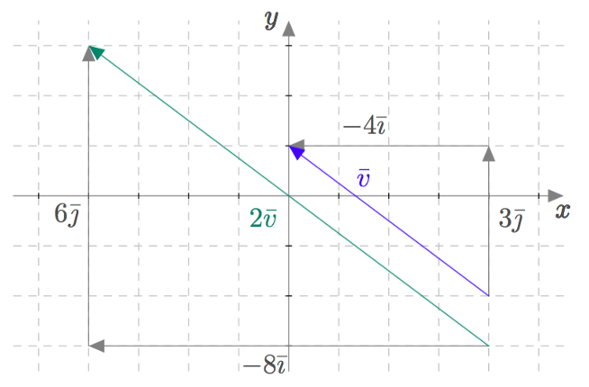
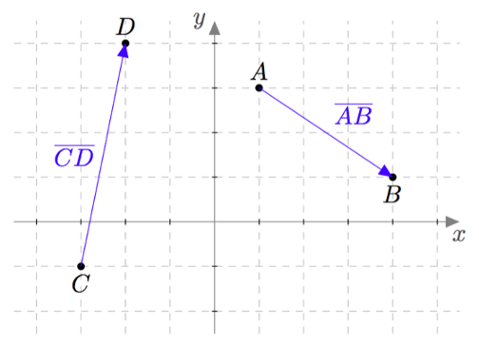
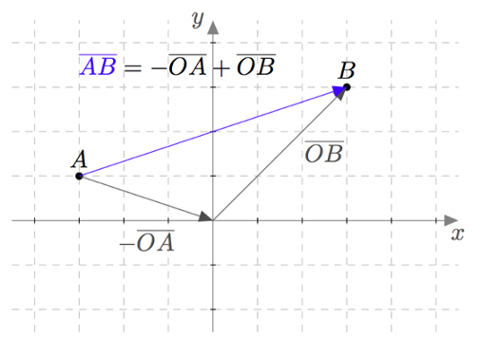
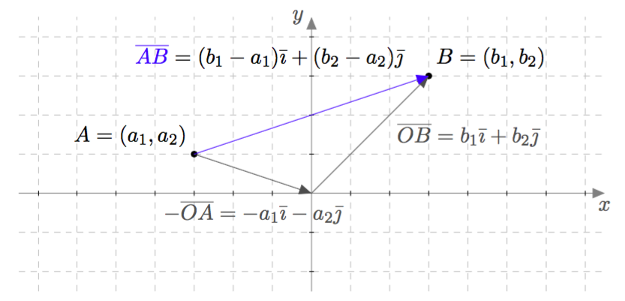
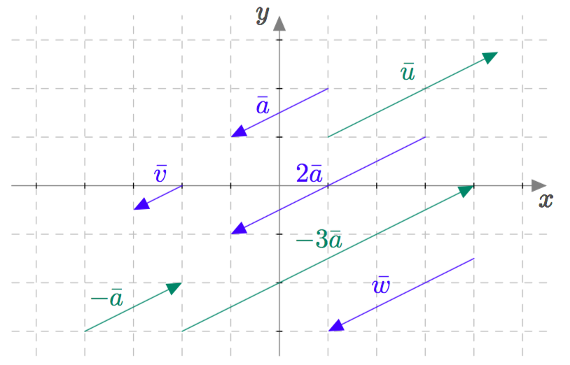
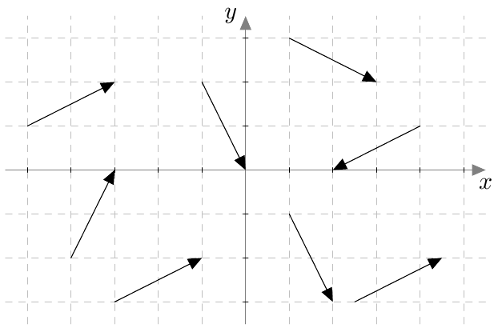
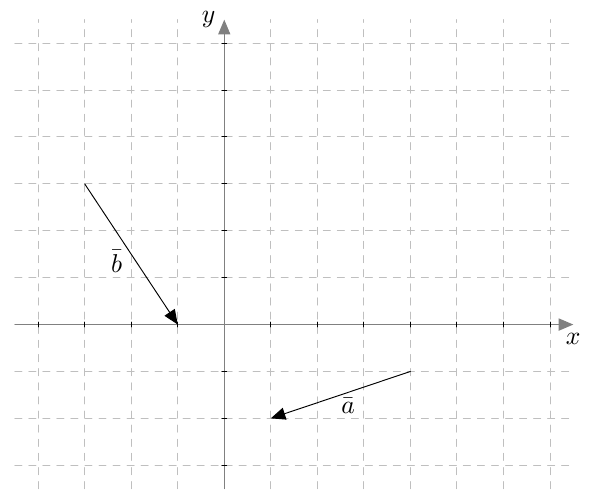
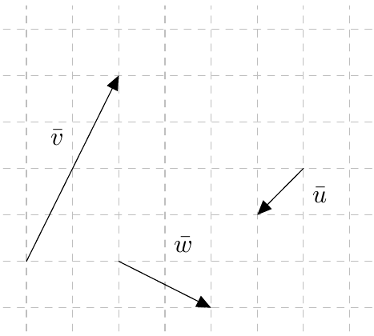
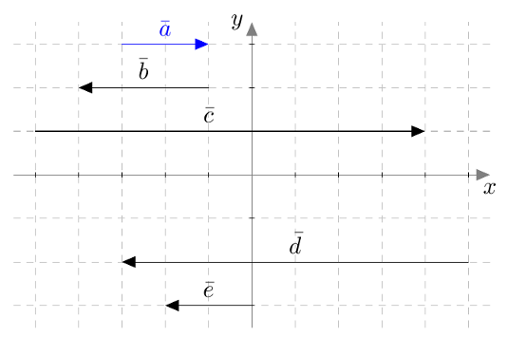
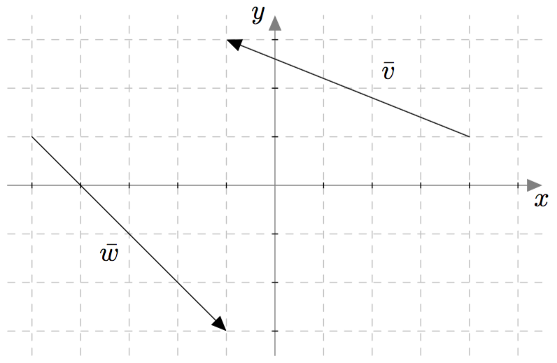
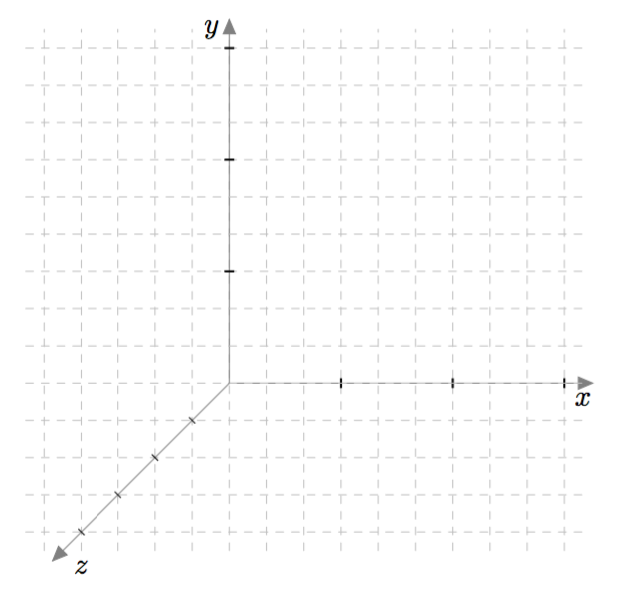
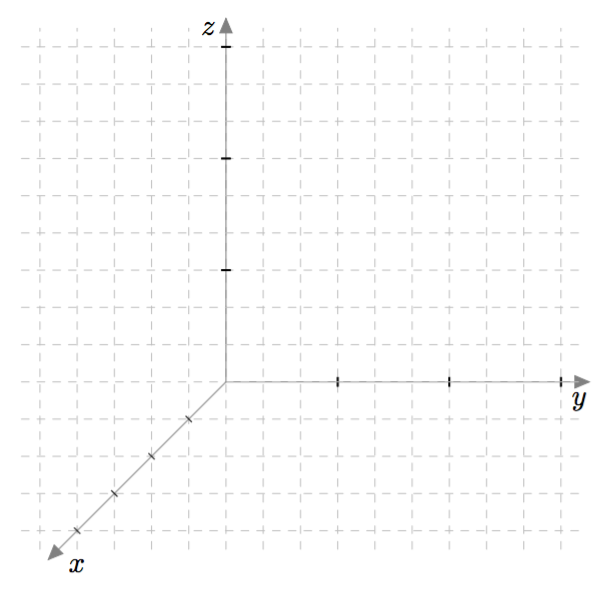
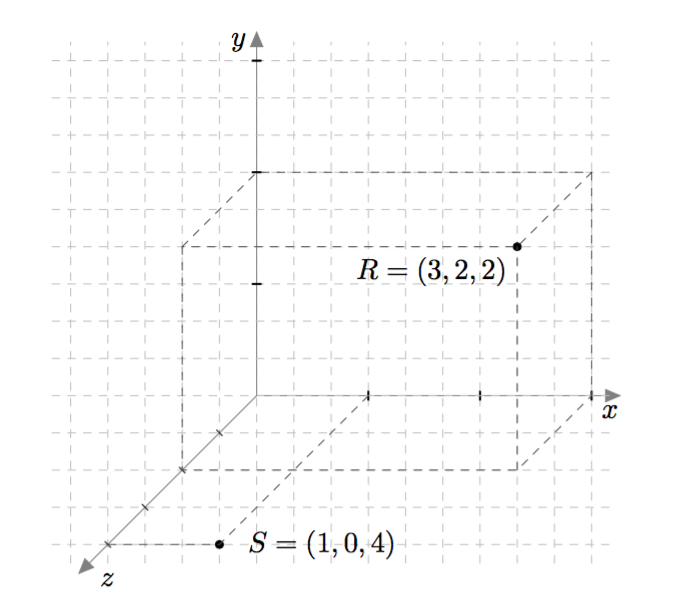
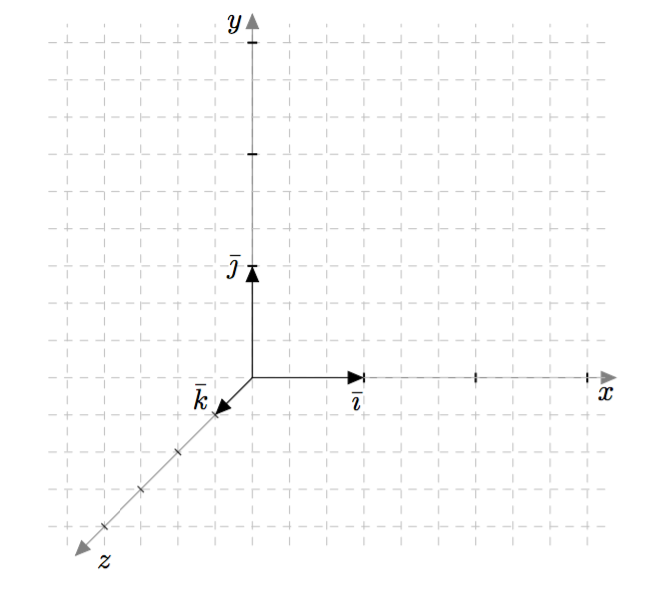
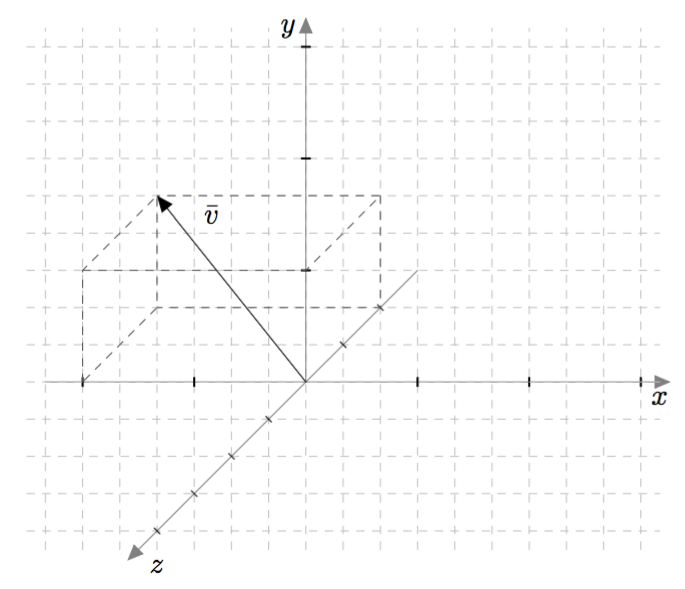
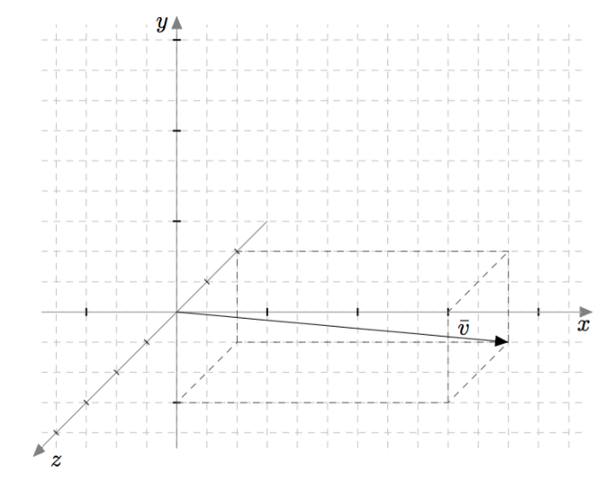
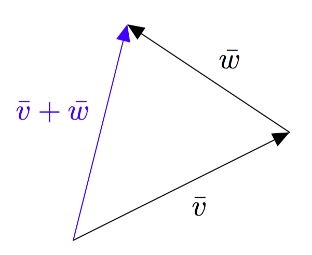
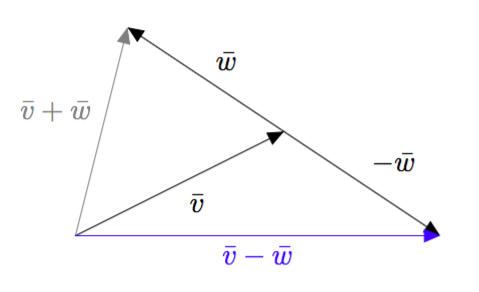
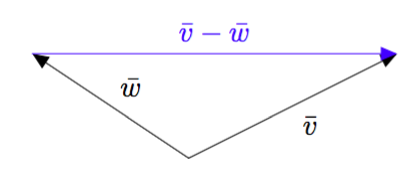
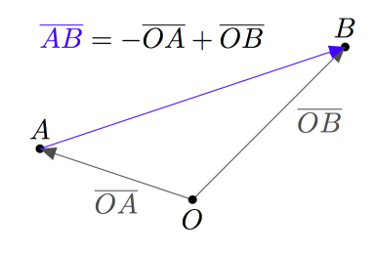
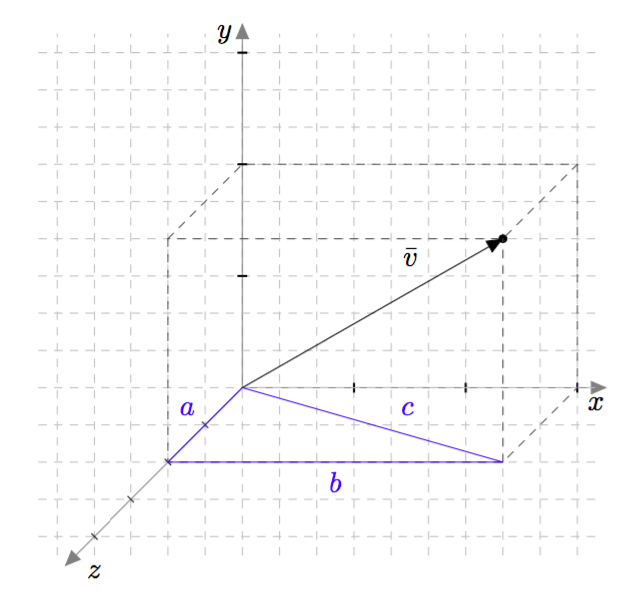
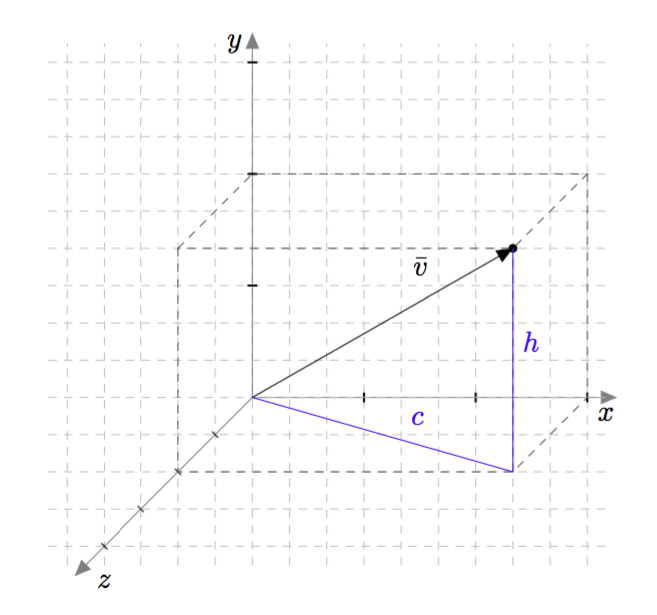
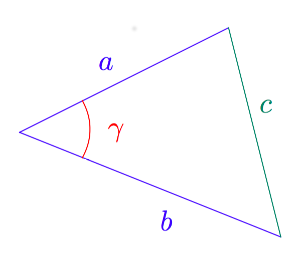
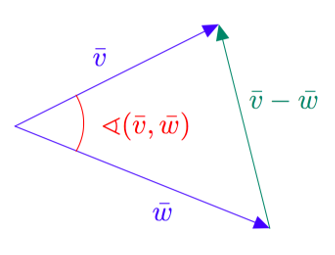
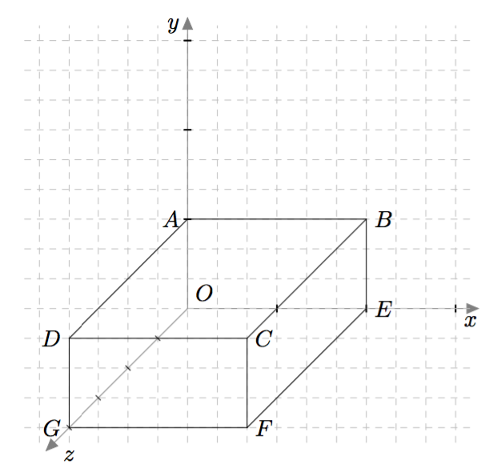
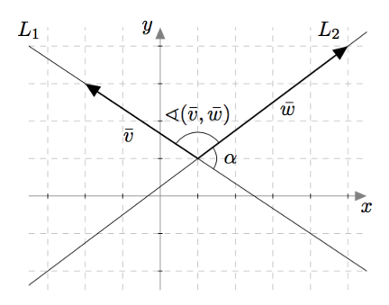
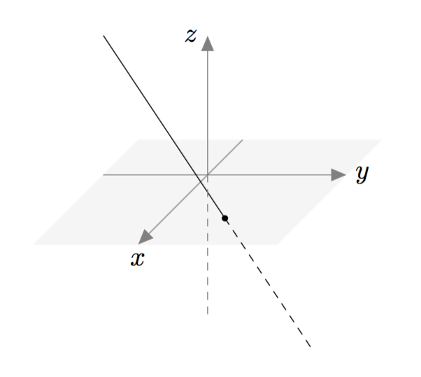
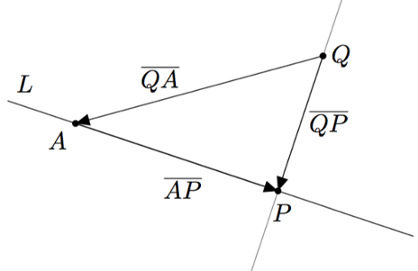
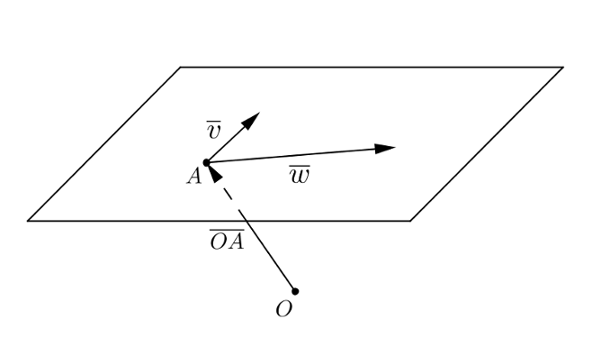
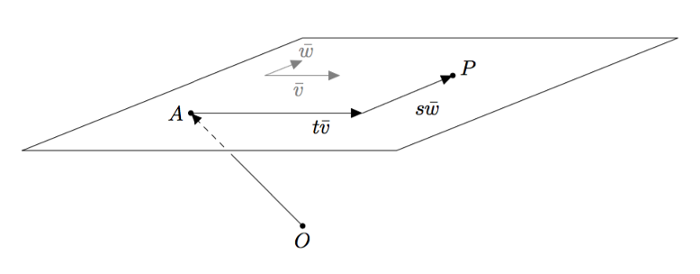
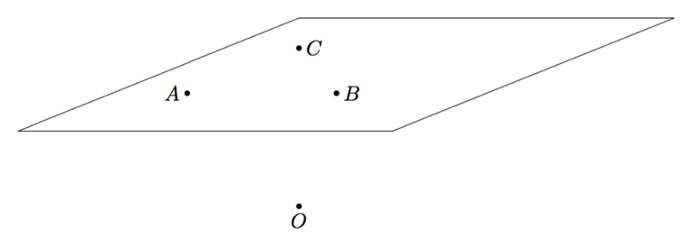
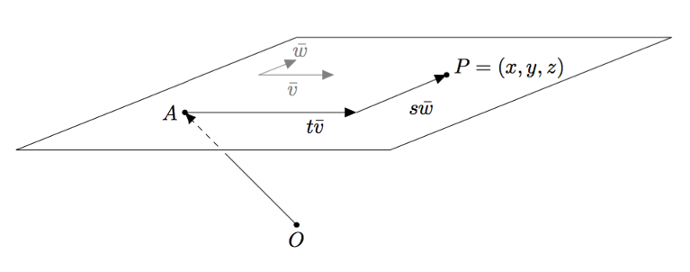
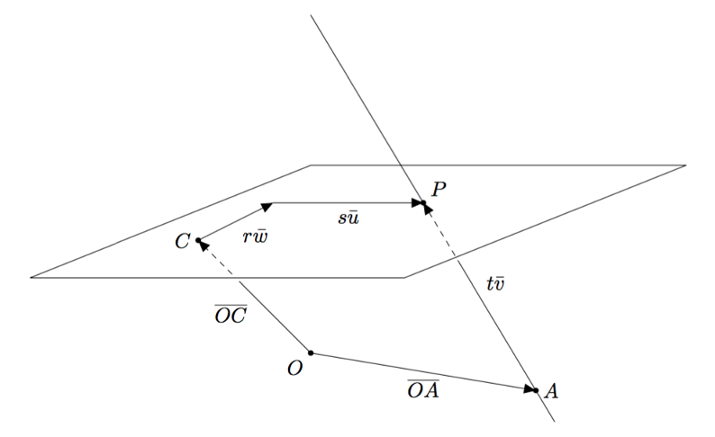
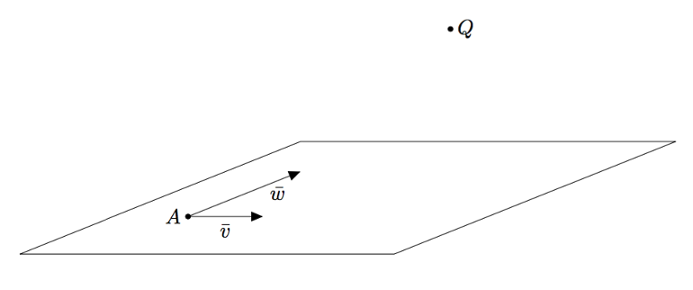
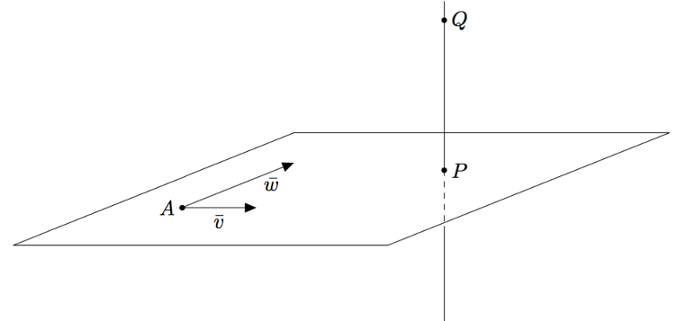
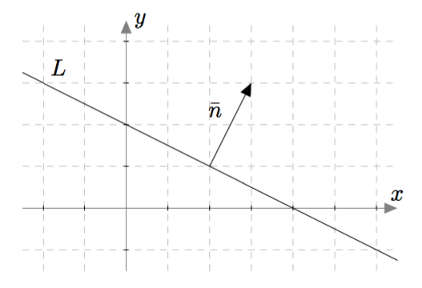
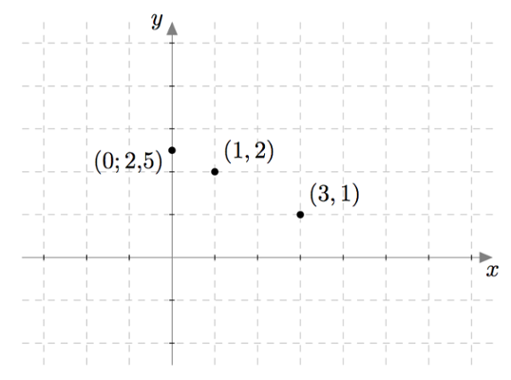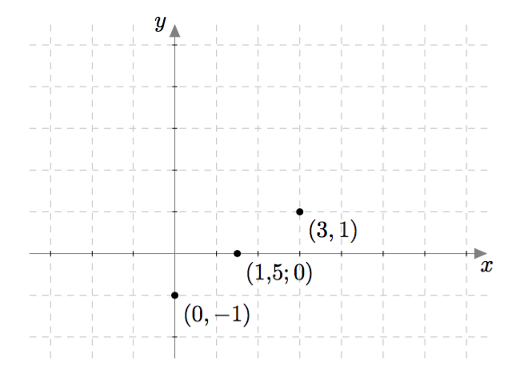Vektoreiden yhdensuuntaisuus määritellään $xyz$-koordinaatistossa samalla tavalla kuin $xy$-tasossa:
MÄÄRITELMÄ: YHDENSUUNTAISUUS
Vektorit $\vv$ ja $\vw$ ovat yhdensuuntaiset eli $\vv \parallel \vw$, jos ja vain jos $\vv=r\vw$ jollakin reaaliluvulla $r \neq 0$.
Vektoreiden yhdensuuntaisuuden tutkiminen johtaa usein yhtälöpariin tai yhtälöryhmään. Esimerkiksi jos halutaan määrittää vakio $t$ niin, että vektorit $\vv = 0{,}5\vi + t\vj + \vk$ ja $\vw = -\vi + 1{,}5\vj-2\vk$ ovat yhdensuuntaisia, on tutkittava yhtälöä $$\vv = r\vw.$$ Tämä yhtälö voidaan kirjoittaa muodossa $$0{,}5\vi + t\vj + \vk = r(-\vi + 1{,}5\vj-2\vk)$$ eli $$0{,}5\vi + t\vj + \vk = -r\vi + 1{,}5r\vj-2r\vk.$$ Vektoreiden samuuden määritelmän mukaan tämä yhtälö toteutuu, jos ja vain jos yhtälön eri puolilla olevat vektorit voidaan ilmaista samalla tavalla vektoreiden $\vi$, $\vj$ ja $\vk$ avulla eli $$ \left\{\begin{aligned} -r &= 0{,}5 \\ 1{,}5r &= t \\ -2r &= 1 \end{aligned}\right. $$ Ratkaistaan nyt tämä yhtälöryhmä eli etsitään kaikki sellaiset luvut $r$ ja $t$, joilla yhtälöryhmän kaikki yhtälöt toteutuvat.
Jos yhtälöryhmän ensimmäisen yhtälön molemmat puolet kerrotaan luvulla $-1$, saadaan yhtälö $$r = -0{,}5.$$ Se voidaan sijoittaa yhtälöryhmän toiseen yhtälöön, joka saadaan silloin kirjoitettua muodossa $$1{,}5\cdot (-0{,}5) = t.$$ Toisin sanottuna $$t = -0{,}75.$$ Tämä tarkoittaa, että yhtälöryhmän ainoa mahdollinen ratkaisu on $r = -0{,}5$ ja $t = -0{,}75$. Vielä on kuitenkin tarkistettava, että se todella on yhtälöryhmän ratkaisu. Tämä tehdään sijoittamalla nämä luvut alkuperäiseen yhtälöryhmään ja tarkistamalla, että kaikki yhtälöt toteutuvat: $$ \left\{\begin{aligned} -(-0{,}5) &= 0{,}5 \\ 1{,}5\cdot (-0{,}5) &= -0{,}75 \\ -2\cdot (-0{,}5) &= 1 \end{aligned}\right. $$ Kaikki yhtälöt toteutuvat, joten yhtälöryhmän $$ \left\{\begin{aligned} -r &= 0{,}5 \\ 1{,}5r &= t \\ -2r &= 1 \end{aligned}\right. $$ ratkaisu on $r = -0{,}5$ ja $t = -0{,}75$.
Yhtälö $$0{,}5\vi + t\vj + \vk = r(-\vi + 1{,}5\vj-2\vk)$$ siis toteutuu, jos ja vain jos $r = -0{,}5$ ja $t = -0{,}75$. Tästä voidaan päätellä, että vektorit $\vv = 0{,}5\vi + t\vj + \vk$ ja $\vw = -\vi + 1{,}5\vj-2\vk$ ovat yhdensuuntaisia, jos ja vain jos $t = -0{,}75$. Tällöin vektorit ovat vastakkaissuuntaisia, koska yhtälössä $\vv = r\vw$ esiintyvä kerroin $r$ on negatiivinen: $r = -0{,}5$.
Tutki, onko olemassa sellainen luku $t$, että vektorit $\vv$ ja $\vw$ ovat yhdensuuntaiset, jos
- $\vv = -\vi + 2\vj$ ja $\vw = 2\vi + t\vj$
- $\vv = 2\vi + 3\vj$ ja $\vw = t(\vi + \vj) - 3(3\vi +\vj)$.
Tarkista tuloksesi järkevyys hahmottelemalla kuva vektoreista $\vv$ ja $\vw$. Jos vektorit ovat yhdensuuntaiset, ovatko ne saman- vai vastakkaissuuntaiset?
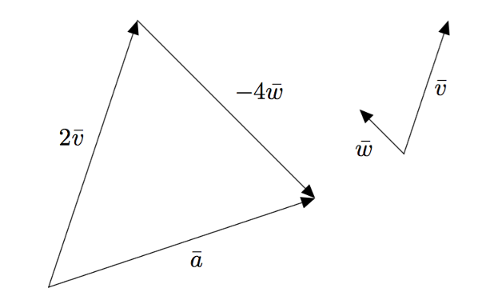
- $t = -4$, jolloin $\vw = -2\vv$ ja vektorit $\vv$ ja $\vw$ ovat vastakkaissuuntaiset.
- $t = 21$, jolloin $\vw = 6\vv$ ja vektorit $\vv$ ja $\vw$ ovat samansuuntaiset.
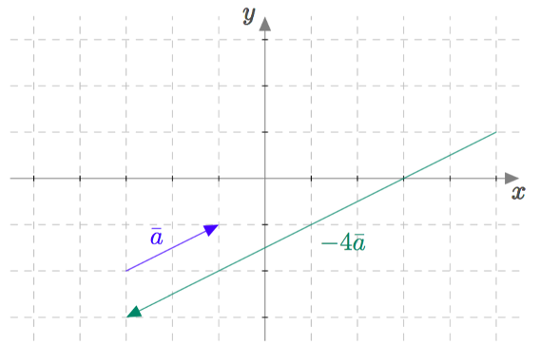
Määritä kaikki sellaiset luvut $t$, joilla vektorit $\vv = 8t\vi + (3t-6)\vj + (6t-4)\vk$ ja $\vw = 4\vi + 3\vj+4\vk$ ovat yhdensuuntaiset. Ovatko vektorit $\vv$ ja $\vw$ tällöin saman- vai vastakkaissuuntaiset?
$t = -2$, jolloin $\vv = -4\vw$ ja vektorit $\vv$ ja $\vw$ ovat vastakkaissuuntaiset.
Tutkitaan seuraavaksi yhtälöparia $$ \left\{\begin{aligned} x+2y &= 5 \\ 2x-3y &= 3. \end{aligned}\right. $$ Se voidaan ratkaista samaan tapaan kuin edellä tehtiin. Ratkaistaan ensin ylemmästä yhtälöstä toinen tuntematon, esimerkiksi $x$. Vähentämällä yhtälön $x + 2y = 5$ molemmilta puolilta $2y$ saadaan yhtälö $$x = 5-2y.$$ Se voidaan sijoittaa alempaan yhtälöön, joka saadaan silloin kirjoitettua muodossa $$2(5-2y) - 3y = 3.$$ Kerrotaan tämän yhtälön vasemmalla puolella sulut auki, jolloin yhtälö saadaan muotoon $$10-4y - 3y = 3.$$ Sieventämällä yhtälön vasen puoli saadaan se muotoon $$10-7y = 3.$$ Vähentämällä yhtälön molemmilta puolilta 10 saadaan uusi yhtälö $$-7y = -7.$$ Jakamalla tämän yhtälön molemmat puolet luvulla $-7$ saadaan $$y = 1.$$ Koska aiempien laskujen mukaan $x = 5-2y$, saadaan $$x = 5-2\cdot 1 = 5-2 = 3.$$ Tämä tarkoittaa, että yhtälöparin ainoa mahdollinen ratkaisu on $x = 3$ ja $y = 1$. Tarkistetaan vielä, että nämä luvut todella toteuttavat kummankin yhtälön: $$ \left\{\begin{aligned} 3+2\cdot 1 &= 3 + 2 = 5 \\ 2\cdot 3-3\cdot 1 &= 6-3 = 3. \end{aligned}\right. $$ Kaikki yhtälöt toteutuvat, joten yhtälöparin $$ \left\{\begin{aligned} x+2y &= 5 \\ 2x-3y &= 3. \end{aligned}\right. $$ ratkaisu on $x = 3$ ja $y = 1$.
Ratkaise yhtälöpari $$ \left\{\begin{aligned} 3x-3y &= 1 \\ x+3y &= 5. \end{aligned}\right. $$
$x = \frac{3}{2}\ $ ja $\ y = \frac{7}{6}$
Edellä tarkastellun yhtälöparin $$ \left\{\begin{aligned} x+2y &= 5 \\ 2x-3y &= 3. \end{aligned}\right. $$ ratkaisua voidaan havainnollistaa seuraavasti: Ensimmäinen yhtälö $x + 2y = 5$ voidaan kirjoittaa muodossa $2y = 5-x$ ja edelleen muodossa $$y = \frac{5-x}{2}.$$ Sen toteuttavia lukupareja $(x,y)$ on vaikka kuinka paljon, sillä luvuksi $x$ voidaan valita mikä tahansa reaaliluku ja sen jälkeen vastaava $y$:n arvo saadaan yllä olevasta yhtälöstä. Esimerkiksi jos $x = 0$, saadaan $$y = \frac{5}{2} = 2{,}5.$$ Jos $x = 1$, saadaan $$y = \frac{4}{2} = 2.$$ Jos $x = 3$, saadaan $$y = \frac{2}{2} = 1.$$ Lukuparit $(0;2{,}5)$, $(1,2)$ ja $(3,1)$ ovat esimerkkejä yhtälön $x + 2y = 5$ ratkaisuista ja niitä voidaan havainnollistaa pisteinä koordinaatistossa:
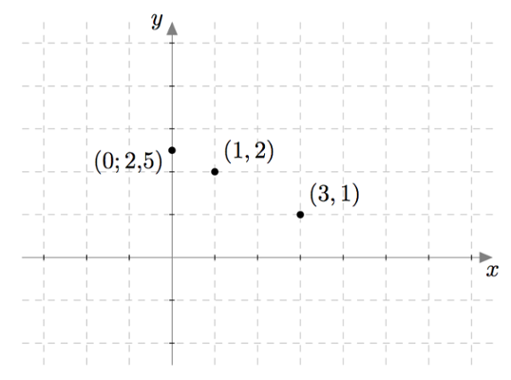
Jos kerätään yhteen kaikki yhtälön $x + 2y = 5$ ratkaisut eli lukuparit, jotka ovat muotoa $$\left(x,\frac{5-x}{2}\right)$$ muodostavat ne koordinaatistoon suoran $$y = \frac{5}{2}-\frac{1}{2}x.$$
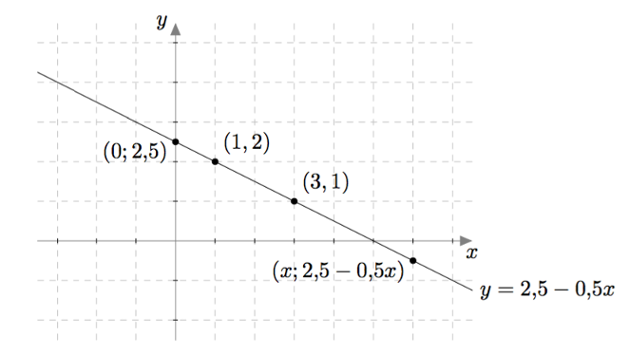
Toinen yhtälö $2x - 3y = 3$ voidaan kirjoittaa muodossa $-3y = 3-2x$ ja edelleen muodossa $$y = \frac{3-2x}{-3}.$$ Sen toteuttavia lukupareja $(x,y)$ on myös vaikka kuinka paljon, sillä luvuksi $x$ voidaan valita mikä tahansa reaaliluku ja sen jälkeen vastaava $y$:n arvo saadaan yllä olevasta yhtälöstä. Esimerkiksi jos $x = 0$, saadaan $$y = \frac{3}{-3} = -1.$$ Jos $x = 1{,}5$, saadaan $$y = \frac{0}{-3} = 0.$$ Jos $x = 3$, saadaan $$y = \frac{-3}{-3} = 1.$$ Lukuparit $(0,-1)$, $(1{,}5;0)$ ja $(3,1)$ ovat esimerkkejä yhtälön $2x - 3y = 3$ ratkaisuista ja niitä voidaan havainnollistaa pisteinä koordinaatistossa:
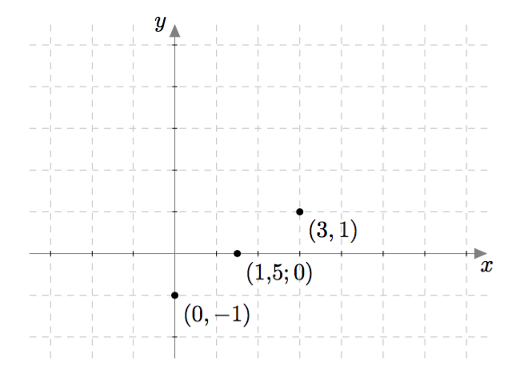
Jos kerätään yhteen kaikki yhtälön $2x - 3y = 3$ ratkaisut eli lukuparit, jotka ovat muotoa $$\left(x,\frac{3-2x}{-3}\right),$$ muodostavat ne koordinaatistoon suoran $$y = -1+\frac{2}{3}x.$$
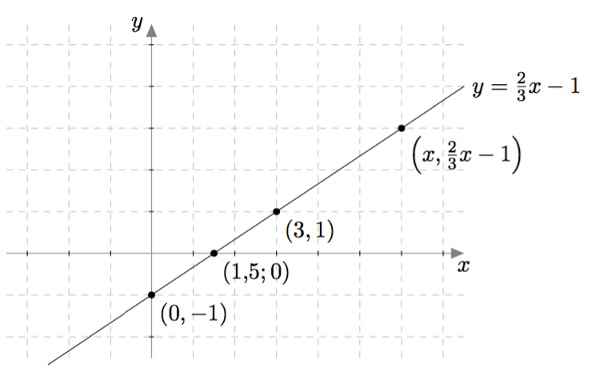
Yhtälöparin $$ \left\{\begin{aligned} x+2y &= 5 \\ 2x-3y &= 3. \end{aligned}\right. $$ ratkaisut ovat täsmälleen ne lukuparit $(x,y)$, jotka toteuttavat sekä yhtälön $x+2y = 5$ että yhtälön $2x-3y = 3$. Toisin sanottuna tutkittavan yhtälöparin ratkaisut ovat näitä yhtälöitä vastaavien suorien leikkauspisteet:
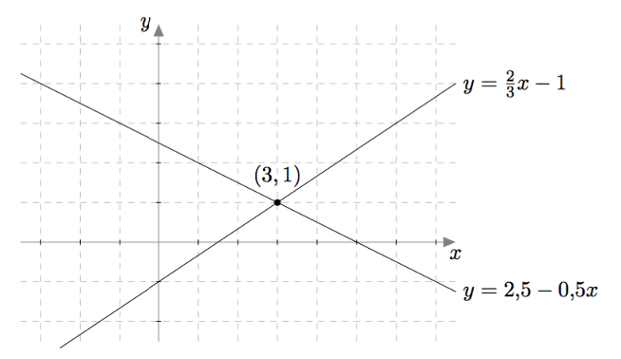
Yllä olevasta kuvasta havaitaan, että yhtälöparilla $$ \left\{\begin{aligned} x+2y &= 5 \\ 2x-3y &= 3. \end{aligned}\right. $$ on tasan yksi ratkaisu, joka määritettiin jo aikaisemmin laskemalla: $x = 3$ ja $y = 1$.
Edellisessä tehtävässä ratkaistiin yhtälöpari $$ \left\{\begin{aligned} 3x-3y &= 1 \\ x+3y &= 5. \end{aligned}\right. $$ Havainnollista ratkaisua piirtämällä koordinaatistoon yhtälöä $3x-3y = 1$ vastaava suora ja yhtälöä $x+3y = 5$ vastaava suora.
Pystyisitkö päättelemään pelkän piirroksen avulla, mitkä luvut toteuttavat tämän yhtälöparin?
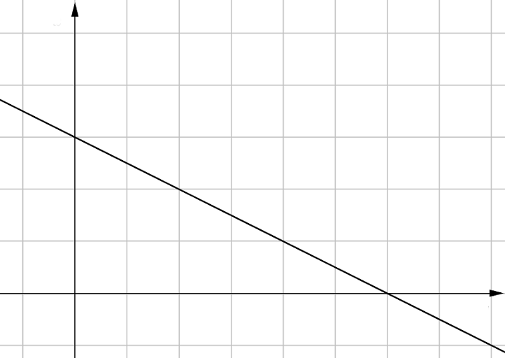
Yhtälöparin ratkaisujen lukumäärää voidaan siis tutkia graafisesti. Esimerkiksi yhtälöpari $$ \left\{\begin{aligned} -2x+y &= -3 \\ 4x-2y &= 3 \end{aligned}\right. $$ voidaan kirjoittaa myös muodossa $$ \left\{\begin{aligned} y &= 2x-3 \\ -2y &= -4x+3 \end{aligned}\right. $$ ja edelleen muodossa $$ \left\{\begin{aligned} y &= 2x-3 \\ y &= 2x-\frac{3}{2}. \end{aligned}\right. $$ Näitä yhtälöitä vastaavat suorat ovat yhdensuuntaiset, kuten alla olevasta kuvasta nähdään:
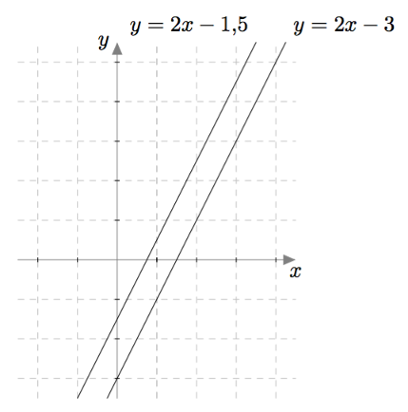
Tarkasteltavalla yhtälöparilla ei siis ole yhtään ratkaisua. Samaan tulokseen päädytään myös laskennallisesti: Yhtälöparin ensimmäinen yhtälö voidaan kirjoittaa muodossa $y = 2x-3$. Jos se sijoitetaan toiseen yhtälöön, saadaan yhtälö $$4x-2(2x-3) = 3.$$ Sieventämällä yhtälön vasenta puolta saadaan $$4x-4x+6 = 3$$ eli $$6 = 3.$$ Tämä yhtälö ei toteudu millään tuntemattomien $x$ ja $y$ arvoilla, joten yhtälöparilla ei ole yhtään ratkaisua.
Ratkaise yhtälöpari $$ \left\{\begin{aligned} 3x+2y &= 6 \\ 9x &= 27-6y. \end{aligned}\right. $$ Havainnollista ratkaisua piirtämällä. Pystyisitkö päättelemään pelkän piirroksen avulla, mitkä luvut toteuttavat tämän yhtälöparin?
Yhtälöparilla ei ole ratkaisua.
Edellä on tarkasteltu yhtälöpareja, jotka ovat muotoa $$ \left\{\begin{aligned} ax+by &= c \\ mx+ny &= k, \end{aligned}\right. $$ missä $a$, $b$, $c$, $m$, $n$ ja $k$ ovat reaalilukuja. Tällaisia yhtälöpareja sanotaan ensimmäisen asteen yhtälöpareiksi. Edellä nähtiin, että tällaisella ensimmäisen asteen yhtälöparilla voi olla tasan yksi ratkaisu tai ei yhtään ratkaisua riippuen siitä, onko yhtälöparia vastaavilla suorilla leikkauspiste vai ei. Näiden vaihtoehtojen lisäksi on vielä kolmaskin mahdollisuus: yhtälöparin kumpikin yhtälö voi vastata samaa suoraa. Tällöin yhtälöparilla on äärettömän paljon ratkaisuja, koska kyseisen suoran jokainen piste on yksi ratkaisu.
Tarkastele yhtälöparia $$ \left\{\begin{aligned} 2y &= 4x-6 \\ 2x-y &= 3. \end{aligned}\right. $$
- Piirrä yhtälöparin ensimmäistä yhtälöä vastaava suora koordinaatistoon.
- Piirrä yhtälöparin toista yhtälöä vastaava suora koordinaatistoon.
- Päättele piirroksesi avulla kolme erilaista ratkaisua yhtälöparille. Tarkista laskemalla, että ne todella ovat ratkaisuja.
- Tiedetään, että $(x,y)$ on yhtälöparin ratkaisu ja $x = 100$. Määritä $y$.
- Tiedetään, että $(x,y)$ on yhtälöparin ratkaisu ja $x = 111$. Määritä $y$.
- Millaista muotoa yhtälöparin ratkaisut $(x,y)$ ovat? Toisin sanottuna jos $x = t$, niin mikä on $y$? (Tässä $t$ on reaaliluku.)
-
-
-
- $y = 197$.
- $y = 219$.
- $(t,2t-3)$.
Yhtälöryhmiä, joissa yhtälöitä ja tuntemattomia on useampia, voidaan ratkaista samaan tapaan kuin edellä ratkaistiin kahden tuntemattoman yhtälöpareja. Esimerkiksi yhtälöryhmää $$ \left\{\begin{aligned} x-3y-2z &= 0 \\ -x+2y-\phantom{2}z &= -5 \\ 3x+4y+\phantom{2}z &= 1 \end{aligned}\right. $$ ratkaistaessa voidaan ensin ratkaista ylimmästä yhtälöstä $x$: $$x = 3y+2z.$$ Se voidaan sijoittaa kahteen alempaan yhtälöön: $$ \left\{\begin{aligned} -(3y+2z)+2y-z &= -5 \\ 3(3y+2z)+4y+z &= 1 \end{aligned}\right. $$ Kertomalla sulut auki yhtälöt saadaan muotoon $$ \left\{\begin{aligned} -3y-2z+2y-z &= -5 \\ 9y+6z+4y+z &= 1. \end{aligned}\right. $$ Sievennetään vielä yhtälöiden vasemmat puolet, jolloin ne näyttävät tältä: $$ \left\{\begin{aligned} -y-3z &= -5 \\ 13y+7z &= 1. \end{aligned}\right. $$ Koko yhtälöryhmä on siis tässä vaiheessa $$ \left\{\begin{aligned} x &= 3y+2z \\ -y-3z &= -5 \\ 13y+7z &= 1. \end{aligned}\right. $$ Ratkaistaan keskimmäisestä yhtälöstä $y$ muutaman välivaiheen kautta, jolloin saadaan $$y = 5-3z.$$ Tässä kannattaa itse miettiä kynän ja paperin kanssa, millaisia välivaiheita ratkaisussa oli. Sijoitetaan saatu $y$:n lauseke alimpaan yhtälöön: $$13(5-3z)+7z = 1.$$ Kertomalla sulut auki yhtälö saadaan muotoon $$65-39z+7z = 1.$$ Tästä saadaan ratkaistua $$-32z = -64$$ eli $$z = \frac{-64}{-32} = 2.$$ Koko yhtälöryhmä on tässä vaiheessa $$ \left\{\begin{aligned} x &= 3y+2z \\ y &= 5-3z \\ z &= 2. \end{aligned}\right. $$ Kun nyt $z$:n arvo tunnetaan, saadaan muut tuntemattomat ratkaistua sen avulla vaiheittain: $$ \left\{\begin{aligned} z &= 2 \\ y &= 5-3z \\ &= 5-3\cdot 2 \\ &= 5-6 \\ &= -1\\ x &= 3y+2z \\ &= 3\cdot(-1) + 2\cdot 2 \\ &= -3+4 \\ &= 1. \end{aligned}\right. $$ Nämä laskut osoittavat, että tarkastellulla yhtälöryhmällä on enintään yksi ratkaisu. Tarkistetaan vielä sijoittamalla, että kaikki yhtälöt todella toteutuvat, jos $x = 1$, $y = -1$ ja $z = 2$: $$ \left\{\begin{aligned} x-3y-2z &=1-3\cdot(-1)-2\cdot 2 \\ &= 1+3-4 \\ &= 4-4 \\ &=0 \\ -x+2y-\phantom{2}z &= -1 + 2\cdot(-1)-2 \\ &= -1-2-2 \\ &= -3-2 \\ &= -5 \\ 3x+4y+\phantom{2}z &= 3\cdot 1 + 4\cdot (-1) + 2 \\ &= 3-4+2 \\ &= -1 + 2 \\ &= 1 \end{aligned}\right. $$ Kaikki yhtälöt toteutuvat, joten yhtälöryhmän ratkaisu on $x = 1$, $y = -1$ ja $z = 2$.
- Ratkaise kynän ja paperin avulla yhtälöryhmä $$ \left\{\begin{aligned} x-2y+3z &= 5 \\ -x+2y-4z &= -4 \\ 6x-\phantom{2}y + 5z &= 10 \end{aligned}\right. $$
- Ratkaise a-kohdan yhtälöryhmä laskimen tai tietokoneen avulla. Katso tarvittaessa mallia tästä videosta.
- $x = 2$, $\ y = -3 \ $ ja $\ z = -1$.
Edellä opeteltiin ratkaisemaan yhtälöryhmiä niin sanotun sijoitusmenetelmän avulla. Yhtälöryhmiä voidaan ratkaista muillakin menetelmillä. Edellisen tehtävän yhtälöryhmä on esimerkki lineaarisesta yhtälöryhmästä, jollaisia voidaan ratkaista myös niin sanotun Gaussin eliminointimenetelmän avulla. Yhden ratkaisutavan hallitseminen kuitenkin riittää tällä kurssilla.