Yhdistetty funktio
Luvun tavoitteet
Tämän luvun tavoitteena on, että tunnet yhdistetyn funktion käsitteen ja sovellat sujuvasti yhdistetyn funktion derivointisääntöä. Osaat
- muodostaa yhdistetyn funktion
- tunnistaa yhdistetystä funktiosta ulko- ja sisäfunktion
- derivoida yhdistetyn funktion
- tutkia funktion kulkua soveltamalla yhdistetyn funktion derivointisääntöä ja MAA6-kurssissa oppimiasi asioita.
Yhdistetty funktio
Edellisessä luvussa tutkittiin erilaisten kertoimien vaikutusta sini- ja kosinifunktioiden kuvaajiin. Samalla nähtiin useita esimerkkejä niin sanotuista yhdistetyistä funktioista. Ne muodostuvat kahdesta funktiosta niin, että ensimmäisen funktion arvo syötetään samantien toiseen funktioon. Esimerkiksi funktio $$ h(x) = \sin 2x $$ saadaan yhdistämällä funktiot $f(x) = 2x$ ja $g(x) = \sin x$: $$ \textcolor{blue}{x} \mapsto \textcolor{red}{2x} \mapsto \sin \textcolor{red}{2x} $$ Tässä tapauksessa funktion $f$ arvo siis lasketaan ensin ja tulos syötetään funktioon $g$ muuttujan paikalle: $$ \textcolor{blue}{x} \mapsto \textcolor{red}{f(x)} \mapsto g(\textcolor{red}{f(x)}). $$ Sitä funktiota, jonka arvo lasketaan ensimmäisenä, sanotaan sisäfunktioksi. Tässä tapauksessa sisäfunktio on siis funktio $f(x) = 2x$. Nimitys juontaa juurensa siitä, että tämä funktio päätyy lopulta toisen funktion sisälle: lopputuloksena tässä tapauksessa on $g(\textcolor{red}{f(x)})$.
MÄÄRITELMÄ: YHDISTETTY FUNKTIO
Funktioista $f$ ja $g$ yhdistetty funktio tarkoittaa funktiota $h$, jonka arvo lasketaan sijoittamalla funktion $f$ arvo muuttujan paikalle funktioon $g$: $$ h(x) = g(f(x)). $$ Tässä funktio $f$ on sisäfunktio ja funktio $g$ on ulkofunktio.
Funktioista $f$ ja $g$ yhdistettyä funktiota merkintään $g \circ f$. Siis $$ (g \circ f)(x) = g(f(x)). $$
Yhdistetyn funktion merkinnässä esiintyä merkki $\circ$ luetaan "pallo": yhdistetyn funktion $g$-pallo-$f$ arvo kohdassa $x$ on funktion $g$ arvo kohdassa $f(x)$.
Yhdistetty funktio
Päättele, mikä on sisäfunktio $f(x)$ ja mikä on ulkofunktio $g(x)$, jos yhdistetylle funktiolle $h(x) = g(f(x))$ pätee
- $h(x) = \cos 3x$
- $h(x) = (x-1)^4$
- $h(x) = \sin^2\! x$
VASTAUS
- Sisäfunktio on $f(x) = 3x$ ja ulkofunktio on $g(x) = \cos x$: $$ \textcolor{blue}{x} \mapsto \textcolor{red}{3x} \mapsto \cos \textcolor{red}{3x} $$
- Sisäfunktio on $f(x) = x-1$ ja ulkofunktio on $g(x) = x^4$: $$ \textcolor{blue}{x} \mapsto \textcolor{red}{x-1} \mapsto (\textcolor{red}{x-1})^4 $$
- Sisäfunktio on $f(x) = \sin x$ ja ulkofunktio on $g(x) = x^2$: $$ \textcolor{blue}{x} \mapsto \textcolor{red}{\sin x} \mapsto (\textcolor{red}{\sin x})^2 = \sin^2\! x $$
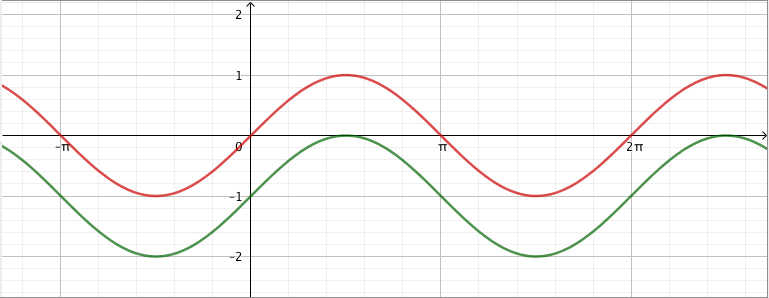
Tämän luvun alussa tarkasteltiin funktioista $f(x) = 2x$ ja $g(x) = \sin x$ yhdistettyä funktiota $(g\circ f)(x) = \sin 2x$. Alla on havainnollistettu kuvaajien avulla tämän yhdistetyn funktion muodostumista. Ensimmäisestä kuvaajasta voidaan lukea, mitä sisäfunktio tekee muuttujalle $x$. Toinen kuvaaja näyttää, mitä ulkofunktio tekee tulokselle $f(x)$.
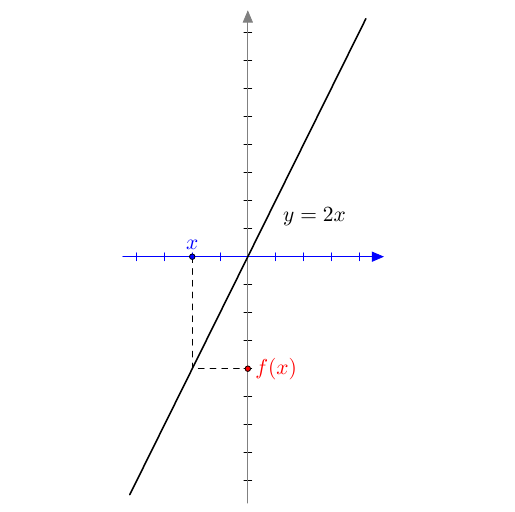
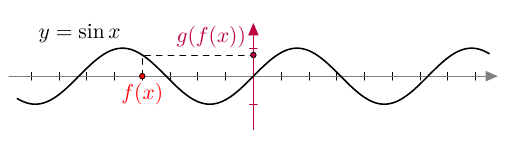
Kun nämä tiedot yhdistetään, saadaan hahmoteltua yhdistetyn funktion kuvaaja:
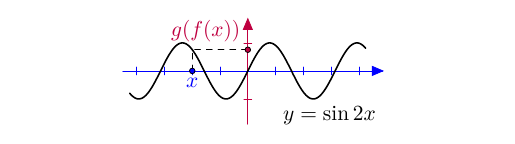
Tutkitaan, mitä tapahtuu, jos funktiot yhdistetään eri järjestyksessä. Otetaan sisäfunktioksi $g(x) = \sin x$ ja ulkofunktioksi $f(x) = 2x$. Alta ensimmäisestä kuvaajasta voidaan lukea, mitä sisäfunktio tekee muuttujalle $x$. Toinen kuvaaja näyttää, mitä ulkofunktio tekee tulokselle $g(x)$.

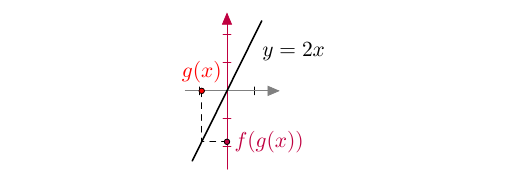
Tässä tapauksessa ulkofunktio siis kaksinkertaistaa sisäfunktion tuloksen. Yhdistetyn funktion lausekkeeksi saadaan $$ (f \circ g)(x) = f(g(x)) = f(\sin x) = 2\sin x. $$
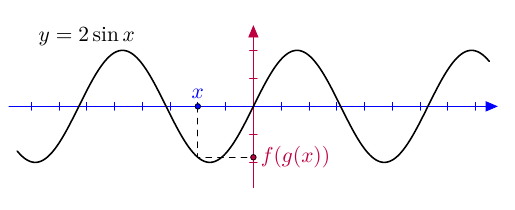
Havaitaan, että yhdistetyt funktiot $g\circ f$ ja $f \circ g$ ovat tässä tapauksessa eri funktiot. Kun funktioita yhdistetään, on siis oltava tarkkana funktioiden järjestyksen kanssa.
Yhdistetty funktio
Merkitään $f(x) = 2 - x$ ja $g(x) = \cos x$. Määritä yhdistetty funktio
- $g \circ f$
- $f \circ g$
VASTAUS
- \begin{align*} (g \circ f)(x) &= g(f(x)) \\ &= g(2-x) \\ &= \cos (2-x) \end{align*}
- \begin{align*} (f \circ g)(x) &= f(g(x)) \\ &= f(\cos x) \\ &= 2 - \cos x \end{align*}
Yhdistetty funktio
Merkitään $f(x) = x^2 - 4$ ja $g(x) = \dfrac{1}{x}$. Muodosta yhdistetty funktio ja päättele, mikä on sen määrittelyjoukko:
- $g \circ f$
- $f \circ g$
VASTAUS
- Yhdistetty funktio on \begin{align*} (g \circ f)(x) &= g(f(x)) \\ &= g(x^2 - 4) \\ &= \frac{1}{x^2 - 4}. \end{align*} Se on määritelty, jos ja vain jos $x\neq 2$ ja $x \neq -2$.
- Yhdistetty funktio on \begin{align*} (f \circ g)(x) &= f(g(x)) \\[2mm] &= f\left(\dfrac{1}{x}\right) \\[2mm] &= \left(\dfrac{1}{x}\right)^2 - 4 \\[2mm] &= \dfrac{1}{x^2} - 4. \end{align*} Se on määritelty, jos ja vain jos $x\neq 0$.
Seuraavassa tehtävässä tarkastellaan yhdistetyn funktion $f(x) = \sin kx$ jaksoa. Kertoimen $k$ vaikutusta sinifunktion jakson pituuteen on tutkittu jo aikaisemmin tehtävissä 2.8 ja 2.9.
Funktion F(X) = SIN KX jakso
Oletetaan, että $k > 0$. Osoita, että kaikilla muuttujan $x$ arvoilla pätee $$ f\!\left(x + \frac{2\pi}{k}\right) = f(x). $$
Vinkki: Sievennä lauseke $$f\!\left(x + \frac{2\pi}{k}\right)$$ mahdollisimman pitkälle. Muista teoreema 13.
VASTAUS
Tehtävän 3.4 avulla saadaan perusteltua seuraava teoreema. Lue teoreema perusteluineen huolellisesti ja mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Oletetaan, että $k > 0$. Yhdistettyjen funktioiden $f(x) = \sin kx$ ja $g(x) = \cos kx$ jakso on $$ \frac{2\pi}{k}. $$
Perustelu: Merkitään funktion $f$ jaksoa kirjaimella $a$.
- Funktion $f$ arvot toistuvat jakson välein: $f(x + a) = f(x)$ eli $$ \sin (kx + ka) = \sin kx. $$ Jos merkitään $z = kx$, yhtälö saadaan muotoon $$ \sin (z + ka) = \sin z. $$ Teoreeman 13 mukaan sinifunktion jakso on $2\pi$, joten $$ka \geq 2\pi$$ (huomaa, että voi olla $ka = 2\pi$ tai $ka = 4\pi$ tai $ka = 6\pi$ tai $\ldots$). Koska $k > 0$, seuraa tästä, että $$ a \geq \frac{2\pi}{k}. $$
- Tehtävässä 3.4 osoitettiin, että kaikilla muuttujan $x$ arvoilla pätee $$ f\left(x + \frac{2\pi}{k}\right) = f(x). $$ Funktion $f$ arvot toistuvat siis aina $\dfrac{2\pi}{k}$ välein, joten funktion $f$ jakso ei voi olla tätä suurempi: $$ a \leq \dfrac{2\pi}{k}. $$
Edellä on päätelty, että $$ \dfrac{2\pi}{k} \leq a \leq \dfrac{2\pi}{k}, $$ joten ainoaksi mahdollisuudeksi jää $$ a = \dfrac{2\pi}{k}. $$ Funktion $g$ jakson pituus perustellaan vastaavalla tavalla.
Seuraavissa tehtävissä harjoitellaan teoreeman 22 soveltamista.
Sinin ja kosinin jaksot
Määritä funktion $h$ arvojoukko ja jakson pituus, jos
- $h(x) = 4 \sin \dfrac{3x}{5}$
- $h(x) = -6 \cos \dfrac{\pi x}{2}$
VASTAUS
- Arvojoukko on $[-4,4]$ ja jakso on $\dfrac{10\pi}{3}$.
- Arvojoukko on $[-6,6]$ ja jakso on $4$.
Sinin ja kosinin jaksot
Tiedetään, että funktion $f(x) = a\sin kx$ jakson pituus on $3$ ja arvojoukko on väli $[-5,5]$. Lisäksi tiedetään, että $k > 0$. Määritä kertoimien $a$ ja $k$ arvot.
VASTAUS
$k = \dfrac{2\pi}{3}$ ja $a = 5$ tai $a = -5$
Annettu funktio voidaan usein tulkita monella eri tavalla yhdistetyksi funktioksi. Esimerkiksi funktio $$ f(x) = \frac{1}{9x^2 + 1} $$ voidaan esittää yhdistettynä funktiona monella eri tavalla riippuen siitä, mikä funktio valitaan sisäfunktioksi. Tätä havainnollistetaan seuraavassa tehtävässä.
Yhdistetty funktio
Tehtävänä on esittää funktio $$ f(x) = \frac{1}{9x^2 + 1} $$ yhdistettynä funktiona $f = u \circ s$. Mikä on ulkofunktio $u(x)$, jos sisäfunktio on
- $s(x) = 9x^2 + 1$
- $s(x) = 9x^2$
- $s(x) = 3x$
VASTAUS
- $u(x) = \dfrac{1}{x}$
- $u(x) = \dfrac{1}{x + 1}$
- $u(x) = \dfrac{1}{x^2 + 1}$
Yhdistetyn funktion derivaatta
Tässä kappaleessa tutkitaan, miten yhdistetyn funktion $g\circ f$ riippuu ulko- ja sisäfunktioiden derivaatoista. Aloitetaan tarkastelemalla yksittäistä esimerkkiä.
Yhdistetyn funktion derivaatta
Tutkitaan funktioita $f(x) = 2x^2$ ja $g(x) = 1 - x^3$.
- Määritä yhdistetty funktio $(g \circ f)(x)$ ja sievennä sen lauseke mahdollisimman pitkälle.
- Määritä a-kohdan funktion derivaattafunktio $(g \circ f)'(x)$.
Vinkki: kertaa tarvittaessa MAA6-kurssin teoreemat 7 ja 9. - Määritä derivaattafunktiot $f'(x)$ ja $g'(x)$.
- Määritä yhdistetty funktio $(g' \circ f)(x)$ ja sievennä sen lauseke mahdollisimman pitkälle.
Vinkki: huomaa, että kysymyksessä on funktiosta $f$ ja derivaattafunktiosta $g'$ muodostettu funktio. - Vertaa b-, c- ja d-kohtien tuloksia. Miten voit muodostaa yhdistetyn funktion derivaattafunktion $(g \circ f)'(x)$ c- ja d-kohtien tuloksista?
VASTAUS
- \begin{align*} (g \circ f)(x) &= g(f(x)) \\ &= g(2x^2) \\ &= 1-(2x^2)^3 \\ &= 1 - 8x^6 \end{align*}
- \begin{align*} (g \circ f)'(x) &= -8\cdot 6x^5 \\ &= -48x^5 \end{align*}
- $f'(x) = 4x$ ja $g'(x) = -3x^2$.
- \begin{align*} (g' \circ f)(x) &= g'(f(x)) \\ &= g'(2x^2) \\ &= -3(2x^2)^2 \\ &= -3\cdot 4x^4 \\ &= -12x^4 \end{align*}
- Havaitaan, että yhdistetyn funktion derivaattafunktio saadaan tulona $(g' \circ f)(x) \cdot f'(x)$ eli $$ (g \circ f)'(x) = g'(f(x)) \cdot f'(x). $$
Testataan edellisen tehtävän tulosta vielä toisessa tapauksessa. Oliko kysymyksessä vain sattuma vai ilmeneekö tässä jokin yleispätevä lainalaisuus?
Yhdistetyn funktion derivaatta
Tutkitaan funktioita $f(x) = x^2-x$ ja $g(x) = x^5$.
- Määritä yhdistetty funktio $(g \circ f)(x)$.
Vinkki: funktion lausekkeen sulkuja ei nyt kannata lähteä avaamaan. - Määritä a-kohdan funktion derivaattafunktio $(g \circ f)'(x)$.
Vinkki: kertaa tarvittaessa MAA6-kurssin teoreema 14. - Määritä derivaattafunktiot $f'(x)$ ja $g'(x)$.
- Määritä funktion $g$ derivaatan arvo kohdassa $f(x)$. Toisin sanottuna määritä $g'(f(x))$.
- Pitääkö tehtävän 3.8 havainto paikkansa tässäkin tapauksessa?
VASTAUS
- \begin{align*} (g \circ f)(x) &= g(f(x)) \\ &= g(x^2 - x) \\ &= (x^2 - x)^5 \end{align*}
- Funktion potenssin derivointisäännön avulla saadaan \begin{align*} (g \circ f)'(x) &= 5(x^2-x)^4(2x-1) \end{align*}
- $f'(x) = 2x-1$ ja $g'(x) = 5x^4$.
- \begin{align*} g'(f(x)) &= g'(x^2-x) \\ &= 5(x^2-x)^4 \end{align*}
- Tehtävän 3.8 havainto pitää paikkansa tässäkin tapauksessa: $$ (g \circ f)'(x) = g'(f(x)) \cdot f'(x). $$
Edellisen tehtävän havainto osoittautuu pitävän paikkansa kaikilla yhdistetyillä funktioilla. Seuraavassa teoreemassa tämä todistetaan tietynlaisille funktioille. Yleinen todistus vaatii keinoja, joihin perehdytään yliopistotasolla.
Lue teoreema ja sen perustelu huolellisesti ja mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Oletetaan, että funktiot $f$ ja $g$ ovat derivoituvia. Yhdistetyn funktion $g \circ f$ derivaatta kohdassa $x$ on ulkofunktion derivaatta kohdassa $f(x)$ kerrottuna sisäfunktion derivaatalla: $$ \mathop{\mathrm{D}} g(f(x)) = g'(f(x))f'(x). $$
Perustelu: Funktion $g \circ f$ erotusosamäärä kohdassa $a$ on $$ \frac{g(f(x)) - g(f(a))}{x-a}. $$ Tehdään lisäoletus, että kohdan $a$ läheisyydessä $f(x) \neq f(a)$. Huomaa, että esimerkiksi vakiofunktioille tämä oletus ei päde, minkä vuoksi tämä perustelu ei ole yleispätevä.
Lisäoletuksesta seuraa, että $f(x) - f(a) \neq 0$ ja erotusosamäärä voidaan laventaa lausekkeella $f(x) - f(a)$: \begin{align*} &\phantom{ {} = {} } \frac{g(f(x)) - g(f(a))}{x-a} \\[2mm] &= \frac{g(f(x)) - g(f(a))}{x-a} \cdot \frac{\textcolor{red}{f(x) - f(a)}}{\textcolor{red}{f(x) - f(a)}} \\[2mm] &= \frac{g(f(x)) - g(f(a))}{\textcolor{red}{f(x) - f(a)}} \cdot \frac{\textcolor{red}{f(x) - f(a)}}{x-a} \end{align*} Jälkimmäinen tulon tekijä on funktion $f$ erotusosamäärä kohdassa $a$: $$ \frac{\textcolor{red}{f(x) - f(a)}}{x-a} \xrightarrow[x\rightarrow a]{} f'(a) $$ Merkitään ensimmäisessä tulon tekijässä $y = f(x)$ ja $b = f(a)$, jolloin saadaan $$ \frac{g(f(x)) - g(f(a))}{\textcolor{red}{f(x) - f(a)}} = \frac{g(y) - g(b)}{y-b}. $$ Tämä on funktion $g$ erotusosamäärä kohdassa $b$: $$ \frac{g(y) - g(b)}{y-b} \xrightarrow[y \rightarrow b]{} g'(b). $$ Koska funktio $f$ on derivoituva, se on jatkuva ja $$ \lim_{x \rightarrow a} f(x) = f(a). $$ Tämä tarkoittaa, että jos $x \rightarrow a$, niin $y \rightarrow b$. Siten \begin{align*} &\phantom{ {} = {} } \frac{g(f(x)) - g(f(a))}{x-a} \\[2mm] &= \frac{g(f(x)) - g(f(a))}{\textcolor{red}{f(x) - f(a)}} \cdot \frac{\textcolor{red}{f(x) - f(a)}}{x-a} \\[2mm] &= \frac{g(y) - g(b)}{y-b} \cdot \frac{\textcolor{red}{f(x) - f(a)}}{x-a} \\[2mm] &\xrightarrow[x \rightarrow a]{} g'(b)f'(a) = g'(f(a))f'(a). \end{align*} Näin on osoitettu, että $$ (g \circ f)'(a) = g'(f(a))f'(a). $$
Yhdistetyn funktion derivointisäännön avulla voidaan derivoida monia trigonometrisia funktioita, joiden derivaattojen määrittäminen muilla tavoin on huomattavasti työläämpää.
Yhdistetyn funktion derivaatta
Tehtävänä on määrittää funktion $h(x) = \sin 2x$ derivaatta.
- Tulkitse funktio $h$ yhdistettynä funktiona $g \circ f$. Mikä on sisäfunktio $f(x)$? Entä ulkofunktio $g(x)$?
- Määritä derivaattafunktiot $f'(x)$ ja $g'(x)$.
- Määritä derivaattafunktion $g'$ arvo kohdassa $f(x)$. Toisin sanottuna määritä $g'(f(x))$.
- Muodosta derivaattafunktio $h'(x)$ teoreeman 23 avulla.
VASTAUS
- Sisäfunktio on $f(x) = 2x$ ja ulkofunktio on $g(x) = \sin x$.
- $f'(x) = 2$ ja $g'(x) = \cos x$.
- $g'(f(x)) = \cos 2x$
- Kysytty derivaattafunktio saadaan yhdistetyn funktion derivointisäännöllä: \begin{align*} h'(x) &= g'(f(x))f'(x) \\ &= (\cos 2x)\cdot 2 \\ &= 2\cos 2x \end{align*}
Yhdistetyn funktion derivaatta
Määritä seuraavat yhdistettyjen funktioiden derivaatat teoreeman 23 avulla:
- $\mathop{\mathrm{D}} \cos 3x$
- $\mathop{\mathrm{D}} \sin (\pi - x)$
- $\mathop{\mathrm{D}} \tan 4x$
VASTAUS
- $\mathop{\mathrm{D}} \cos 3x = -3\sin 3x$
- $\mathop{\mathrm{D}} \sin (\pi - x) = -\cos (\pi - x)$
- $\mathop{\mathrm{D}} \tan 4x = 4(1 + \tan^2\! 4x)$ tai $$\mathop{\mathrm{D}} \tan 4x = \dfrac{4}{\cos^2\! 4x}$$
Teoreeman 23 perustelussa tehtiin lisäoletus, että kohdan $a$ läheisyydessä $f(x) \neq f(a)$. Esimerkiksi vakiofunktioille tämä oletus ei päde. Perustelu ei siis ole yleispätevä, vaan se todistaa väitteen vain sellaisille funktioille, joilla lisäoletuksen ehto toteutuu. Seuraavassa tehtävässä tutkitaan, mitä tapahtuu, jos yhdistetyssä funktiossa sisäfunktiona on vakiofunktio.
Yhdistetyn funktion derivaatta
Tarkastellaan yhdistettyä funktiota $g \circ f$ tilanteessa, jossa sisäfunktiona on vakiofunktio $f(x) = 3$. Ulkofunktio voi tässä olla mikä tahansa funktio. Toisin sanottuna tarkastellaan tilannetta, jossa ulkofunktiosta $g$ ei ole tarkempaa tietoa.
- Muodosta yhdistetyn funktion $g \circ f$ lauseke ja sievennä se mahdollisimman pitkälle. Millainen funktio $g \circ f$ on?
- Päättele yhdistetyn funktion $g \circ f$ derivaatta a-kohdan avulla.
Vinkki: MAA6-kurssin teoreema 6. - Mikä on funktion $f$ derivaatta?
- Päättele c-kohdan avulla, mitä on $g'(f(x))f'(x)$. Vertaa tulosta b-kohdan tulokseen. Päteekö yhdistetyn funktion derivointisääntö tässä tapauksessa? Toisin sanottuna, saitko saman tuloksen kuin b-kohdassa?
VASTAUS
- $(g\circ f)(x) = g(f(x)) = g(3)$ kaikilla $x$, joten yhdistetty funktio on vakiofunktio. Sen arvoa ei kuitenkaan voi annettujen tietojen avulla päätellä. Arvo riippuu siitä, mikä on funktion $g$ arvo kohdassa 3.
- Vakiofunktion derivaatta on nollafunktio, joten $(g\circ f)'(x) = 0$.
- Funktio $f$ on vakiofunktio, joten $f'(x) = 0$.
- $g'(f(x))f'(x) = g'(3) \cdot 0 = 0$.
Tulos on sama kuin kohdassa (b), joten yhdistetyn funktion derivointisääntö $$ (g\circ f)'(x) = g'(f(x))f'(x) $$ pätee tässä tapauksessa.
Seuraavissa tehtävissä harjoitellaan vielä teoreeman 23 soveltamista.
Yhdistetyn funktion derivaatta
Jatkoa tehtävään 2.45. Sataman veden syvyys vaihtelee nousu- ja laskuveden myötä 12 tunnin jaksoissa. Syvyys on suurimmillaan 5,2 metriä ja pienimmillään 2,4 metriä. Veden syvyyttä (metreinä) voidaan kuvata funktiolla $$ f(t) = 3{,}8 + 1{,}4 \cos \left(\dfrac{\pi t}{6}\right). $$ Tässä ajanhetki $t = 0$ (tuntia) on valittu niin, että silloin vesi on korkeimmillaan. Millä nopeudella vedenpinta nousee tai laskee, kun nousuveden huipusta on kulunut
- yksi tunti
- 8 tuntia
- 9 tuntia?
VASTAUS
Derivaattafunktio on $$ f'(t) = -1{,}4 \cdot \frac{\pi}{6} \sin \left(\dfrac{\pi t}{6}\right). $$
- $f'(1) \approx -0{,}37$ eli vedenpinta laskee noin 37 cm tunnissa.
- $f'(8) \approx 0{,}63$ eli vedenpinta nousee noin 63 cm tunnissa.
- $f'(9) \approx 0{,}73$ eli vedenpinta nousee noin 73 cm tunnissa.
Yhdistetyn funktion derivaatta
Funktion $$ f(x) = 3 \sin \left(\frac{x}{2}\right) $$ kuvaajalle piirretään tangentti kohtaan $$x = \frac{8\pi}{3}.$$ Määritä tangentin yhtälö.
VASTAUS
Derivaattafunktion on $$ f'(x) = \frac{3}{2} \cos \left(\frac{x}{2}\right), $$ joten tangentin kulmakerroin on \begin{align*} f'\left(\frac{8\pi}{3}\right) &= \frac{3}{2} \cos \left(\frac{4\pi}{3}\right) \\[2mm] &= -\frac{3}{4} \end{align*} Funktion kuvaajan pisteen $y$-koordinaatti on \begin{align*} f\left(\frac{8\pi}{3}\right) &= 3 \sin \left(\frac{4\pi}{3}\right) \\[2mm] &= -\frac{3}{2}\sqrt{3} \end{align*} Tangentin yhtälö on $$ y - \left(-\frac{3}{2}\sqrt{3}\right) = -\frac{3}{4}\left(x - \frac{8\pi}{3}\right) $$ eli $$ y = -\frac{3}{4}x + 2\pi - \frac{3}{2}\sqrt{3}. $$
Funktion kulku
Tässä luvussa perehdytään erilaisiin tapoihin tutkia trigonometristen funktioiden kulkua. Päättelyssä voidaan tilanteesta riippuen hyödyntää sinin ja kosinin ominaisuuksia, yksikköympyrää tai derivaattaa.
Jos funktion lausekkeessa esiintyy vain yksittäinen sini tai kosini, voidaan funktion suurin ja pienin arvo selvittää sinin tai kosinin ominaisuuksien avulla. Tätä harjoitellaan seuraavassa tehtävässä.
Suurin ja pienin arvo
Tutkitaan funktiota $$ h(x) = \cos (3x) + 2. $$ Tehtävänä on selvittää sen suurin ja pienin arvo sekä jakso.
- Palauta mieleesi tavallisen kosinifunktion $f(x) = \cos x$ suurin ja pienin arvo. Mikä on tavallisen kosinifunktion jakso?
Vinkki: teoreema 14. - Tarkastellaan yhdistettyä funktiota $g(x) = \cos(3x)$. Mikä on sen suurin arvo? Entä pienin? Mikä on sen jakso?
Vinkki: tehtävä 2.15 ja teoreema 22. - Mikä on funktion $h(x) = \cos(3x) + 2$ suurin arvo? Entä pienin? Mikä on sen jakso?
Vinkki: tehtävä 2.16. - Piirrä funktioiden $f$, $g$ ja $h$ kuvaajat Geogebralla ja tarkista, että päättelysi ei ole ristiriidassa kuvaajien kanssa.
VASTAUS
- Tavallisen kosinifunktion $f(x) = \cos x$ suurin arvo on $1$ ja pienin arvo on $-1$. Sen jakso on $2\pi$.
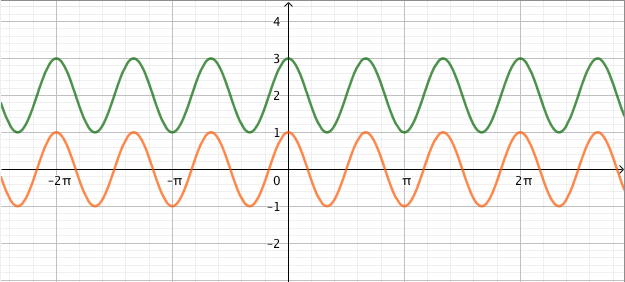
- Funktion $g(x) = \cos(3x)$ suurin arvo on $1$ ja pienin arvo on $-1$. Sisäfunktion kerroin 3 vaikuttaa vain jakson pituuteen, ei suurimpaan eikä pienimpään arvoon. Funktion $g$ jakso on $$ \frac{2\pi}{3}. $$
- Funktion $h(x) = \cos(3x) + 2$ suurin arvo on $$1 + 2 = 3$$ ja pienin arvo on $$-1 + 2 = 1.$$ Vakio $2$ vaikuttaa kuvaajan sijaintiin koordinaatistossa, mutta ei sen muotoon. Funktion $h$ jakso on siten sama kuin funktion $g$ jakso eli $$ \frac{2\pi}{3}. $$
- Tavallisen kosinifunktion kuvaaja:
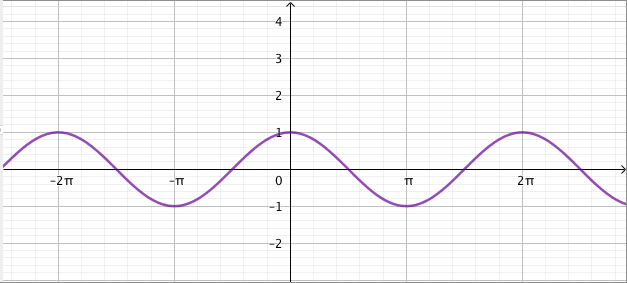
Funktioiden $g(x) = \cos(3x)$ ja $h(x) = \cos(3x) + 2$ kuvaajat:
Yksikköympyrän avulla sinin ja kosinin arvoja voidaan tarkastella vielä yksityiskohtaisemminkin. Seuraavat tehtävät havainnollistavat asiaa.
Funktion arvojoukko
Tutkitaan funktiota $$ g(x) = \sin \left(\dfrac{x}{6}\right) - 1, $$ missä $\pi < x < 7\pi$. Tehtävänä on selvittää funktion arvojoukko.
- Merkitään $$ z = \dfrac{x}{6}, $$ jolloin voidaan kirjoittaa $$g(z) = \sin(z) - 1.$$ Tehtävässä sanotaan, että $$\pi < x < 7\pi.$$ Päättele, millä välillä $z$ on.
- Selvitä yksikköympyrän avulla, mitä arvoja tavallinen sinifunktio $$f(z) = \sin z$$ saa, kun muuttuja $z$ on a-kohdassa päättelemälläsi välillä.
- Päättele b-kohdan avulla, mitä arvoja funktio $$g(z) = \sin(z) - 1$$ saa, kun muuttuja $z$ on a-kohdassa päättelemälläsi välillä.
- Mitä arvoja funktio $$g(x) = \sin \left(\dfrac{x}{6}\right) - 1$$ saa, kun $\pi < x < 7\pi$?
Vinkki: vertaa c-kohtaan.
VASTAUS
- Jos $\pi < x < 7\pi$, niin $$\dfrac{\pi}{6} < \dfrac{x}{6} < \dfrac{7\pi}{6}$$ eli $$\dfrac{\pi}{6} < z < \dfrac{7\pi}{6}.$$
- Kun $$\dfrac{\pi}{6} < z < \dfrac{7\pi}{6},$$ niin tavallinen sinifunktio $f(z) = \sin z$ saa arvot väliltä $$\left] -\frac{1}{2}, 1\right].$$ Tämä voidaan päätellä alla olevasta yksikköympyrästä ja siitä, että $$ \sin\left(\frac{7\pi}{6}\right) = -\dfrac{1}{2}. $$
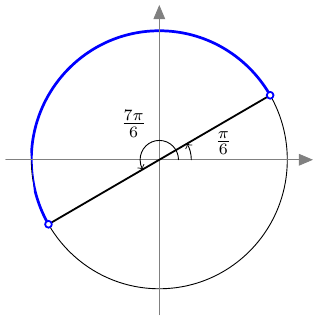
- Kun $$\dfrac{\pi}{6} < z < \dfrac{7\pi}{6},$$ niin funktio $g(z) = \sin (z) - 1$ saa arvot väliltä $$\left] -\frac{3}{2}, 0\right].$$
- Kun $\pi < x < 7\pi$, niin funktio \begin{align*} g(x) &= \sin \left(\dfrac{x}{6}\right) - 1 \end{align*} saa arvot väliltä $$\left] -\frac{3}{2}, 0\right].$$
Funktion kulku
Tutkitaan edelleen funktiota $$ g(x) = \sin \left(\dfrac{x}{6}\right) - 1, $$ missä $\pi < x < 7\pi$. Tehtävänä on selvittää, missä funktio on kasvava ja missä vähenevä.
- Merkitään $$ z = \dfrac{x}{6}, $$ jolloin voidaan kirjoittaa $$ g(z) = \sin(z) - 1. $$ Miten tämän funktion kuvaaja eroaa tavallisen sinifunktion $$f(z) = \sin z$$ kuvaajasta? Selitä omin sanoin. Voit piirtää kummankin funktion kuvaajat, jos haluat.
- Tehtävässä 3.16 pääteltiin, että kun $\pi < x < 7\pi$, niin $$\dfrac{\pi}{6} < z < \dfrac{7\pi}{6}.$$ Päättele yksikköympyrän avulla, missä tavallinen sinifunktio $$f(z) = \sin z$$ on kasvava ja missä vähenevä, kun $$\dfrac{\pi}{6} < z < \dfrac{7\pi}{6}.$$
- Päättele a- ja b-kohtien avulla, missä funktio $$ g(z) = \sin(z) - 1. $$ on kasvava ja missä vähenevä, kun $$\dfrac{\pi}{6} < z < \dfrac{7\pi}{6}.$$
- Millä välillä muuttuja $x$ on, kun funktio $g$ on kasvava? Entä millä välillä muuttuja $x$ on, kun funktio $g$ on vähenevä?
VASTAUS
- Funktion $g$ kuvaaja on koordinaatistossa yhden yksikön verra funktion $f$ kuvaajan alapuolella. Muuten kuvaajat ovat samanlaiset.
- Sinifunktio $f(z) = \sin z$ on kasvava, kun $$ \dfrac{\pi}{6} < z \leq \dfrac{\pi}{2}. $$ Alla olevasta yksikköympyrästä havaitaan, että kun kulma kasvaa tällä välillä, myös sinin arvot kasvavat.

Sinifunktio $f(z) = \sin z$ on vähenevä, kun $$ \dfrac{\pi}{2} \leq z < \dfrac{7\pi}{6}. $$ Yllä olevasta yksikköympyrästä havaitaan, että kun kulma kasvaa tällä välillä, niin sinin arvot pienenevät. - Funktio $$ g(z) = \sin(z) - 1. $$ on kasvava, kun $$ \dfrac{\pi}{6} < z \leq \dfrac{\pi}{2} $$ ja vähenevä, kun $$ \dfrac{\pi}{2} \leq z < \dfrac{7\pi}{6}. $$
- Funktio $g$ on kasvava, kun $$ \frac{\pi}{6} < \frac{x}{6} \leq \frac{\pi}{2} $$ eli $$ \pi < x \leq 3\pi. $$ Funktio $g$ on vähenevä, kun $$ \frac{\pi}{2} \leq \dfrac{x}{6} < \frac{7\pi}{6} $$ eli $$ 3\pi \leq x < 7\pi. $$
Jos funktio lausekkeessa esiintyy useampi erilainen sini tai kosini, funktion kulun tutkimiseen tarvitaan yleensä derivaattaa. Tarkastellaan esimerkiksi funktiota $$ f(x) = \sin x + \cos^2 x. $$ Aloitetaan määrittämällä tämän funktion jakso. Tarkastellaan aluksi jokaista yhteenlaskettavaa erikseen. Tiedetään, että sinifunktion $$ x \mapsto \sin x $$ jakso on $2\pi$. Yksikköympyrästä voidaan havaita, että kosinilla pätee yhtälö $$ \cos (x + \pi) = -\cos x. $$ Toiseen potenssiin korotus hävittää miinusmerkin, joten toiset potenssit ovat samat: $$ \cos^2 (x + \pi) = \cos^2 x. $$ Tästä voidaan päätellä, että funktion $$ x \mapsto \cos^2 x $$ jakso on $\pi$. Funktioiden kuvaajat tukevat tätä päättelyä:
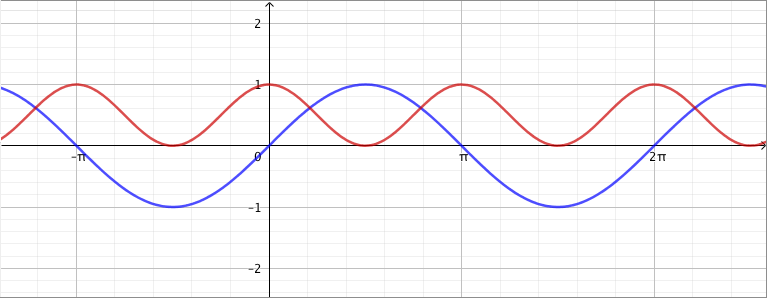
Sinifunktion jakso on siis pitempi ja sisältää tasan kaksi funktion $x \mapsto \cos^2 x$ jaksoa. Siten summafunktio $f$ ehtii sinin jakson aikana saada kaikki mahdolliset arvonsa. Tästä voidaan päätellä, että funktion $f$ jakso on $2\pi$. Kuva tukee johtopäätöstä:
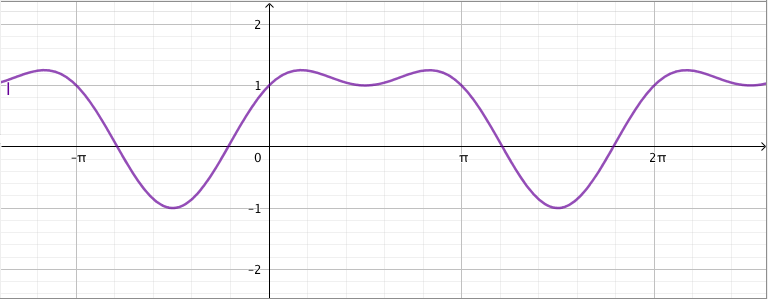
Funktion arvot toistuvat samanlaisina aina jakson välein. Tämän vuoksi riittää tarkastella suljettua väliä, jonka pituus on $2\pi$. Koska funktio on jatkuva, se saa suurimman ja pienimmän arvonsa tällaisen välin päätepisteissä tai derivaatan nollakohdissa.
Suurin ja pienin arvo
Jatketaan funktion $$ f(x) = \sin x + \cos^2 x $$ tarkastelua. Tehtävänä on määrittää sen suurin ja pienin arvo.
- Valitse jokin suljettu väli, jonka pituus on funktion $f$ jakso $2\pi$.
- Määritä derivaattafunktio $f'(x)$.
- Selvitä, mitä nollakohtia derivaattafunktiolla on a-kohdassa valitsemallasi välillä.
- Laske funktion arvo valitsemasi välin päätepisteissä ja välille osuvissa derivaatan nollakohdissa. Mikä on funktion suurin arvo? Entä pienin?
VASTAUS
- Väli voi olla esimerkiksi $[0, 2\pi]$.
- $f'(x) = \cos x - 2\cos x \sin x$
- Välillä $[0, 2\pi]$ derivaattafunktiolla on nollakohdat $$\dfrac{\pi}{6}, \ \dfrac{\pi}{2}, \ \dfrac{5\pi}{6} \ \text{ ja } \ \dfrac{3\pi}{2}.$$ Ne löydetään ratkaisemalla yhtälö $$ \cos x\, (1 - 2\sin x) = 0. $$
- Lasketaan arvot: \begin{align*} f\left(0\right) &= 1 \\[1mm] f\left(\frac{\pi}{6}\right) &= \frac{5}{4} \\[1mm] f\left(\frac{\pi}{2}\right) &= 1 \\[1mm] f\left(\frac{5\pi}{6}\right) &= \frac{5}{4} \\[1mm] f\left(\frac{3\pi}{2}\right) &= -1 \\[1mm] f\left(2\pi\right) &= 1 \end{align*} Funktion $f$ pienin arvo on $-1$ ja suurin arvo on $\dfrac{5}{4}$.
Suurin ja pienin arvo
Tarkastellaan funktiota $$ f(x) = \cos 2x - 4 \cos x. $$ Tehtävänä on määrittää sen suurin ja pienin arvo.
- Mikä on tavallisen kosinifunktion jakso? Entä mikä on funktion $x \mapsto \cos 2x$ jakso? Päättele näiden tietojen avulla, mikä on funktion $f$ jakso.
- Valitse jokin suljettu väli, jonka pituus on sama kuin funktion $f$ jakso.
- Määritä derivaattafunktio $f'(x)$. Selvitä, mitä nollakohtia derivaattafunktiolla on b-kohdassa valitsemallasi välillä.
Vinkki: nollakohtien ratkaisemisessa auttaa teoreema 17. - Mikä on funktion suurin arvo? Entä pienin?
- Tarkista päättelysi piirtämällä funktion $f$ kuvaaja esimerkiksi Geogebralla.
VASTAUS
- Kosinifunktion jakso on $2\pi$. Funktion $x \mapsto \cos 2x$ jakso on $$ \dfrac{2\pi}{2} = \pi. $$ Tämä sisältyy tasan kaksi kertaa kosinifunktion jaksoon, joten funktion $f$ jakso on sama kuin kosinifunktiolla eli $2\pi$.
- Väli voi olla esimerkiksi $[0, 2\pi]$.
- Derivaattafunktio on $$f'(x) = -2\sin 2x + 4\sin x.$$ Kaksinkertaisen kulman sinin kaavan avulla (teoreema 17) se saadaan muotoon $$ f'(x) = -4\sin x \cos x + 4\sin x. $$ Välillä $[0, 2\pi]$ derivaattafunktiolla on nollakohdat $0$, $\pi$ ja $2\pi$. Ne löydetään ratkaisemalla yhtälö $$ -4\sin x (\cos x - 1) = 0. $$
- Lasketaan arvot derivaatan nollakohdissa ja tarkasteluvälin päätepisteissä: \begin{align*} f\left(0\right) &= -3 \\[1mm] f\left(\pi\right) &= 5 \\[1mm] f\left(2\pi\right) &= -3 \end{align*} Funktion $f$ pienin arvo on $-3$ ja suurin arvo on $5$.
- Funktion $f$ kuvaaja:
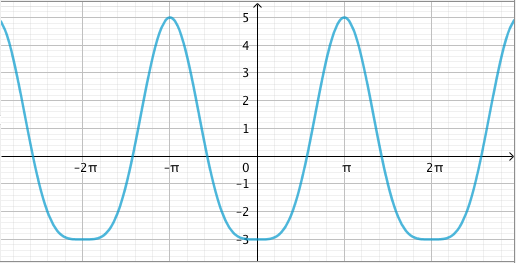
TEHTÄVÄSARJA II
Yhdistetty funktio
Muodosta lauseke yhdistetylle funktiolle $u \circ s$ ja sievennä se mahdollisimman pitkälle, jos
- $u(x) = (x-1)^2$ ja $s(x) = 1 + 2x$
- $u(x) = 1 + 2x$ ja $s(x) = (x-1)^2$
VASTAUS
- $u(s(x)) = 4x^2$
- $u(s(x)) = 2x^2 - 4x + 3$
Yhdistetty funktio
Päättele, mikä on sisäfunktio $s(x)$ ja mikä on ulkofunktio $u(x)$, jos yhdistetylle funktiolle $f = u\circ s$ pätee
- $f(x) = \dfrac{1}{\tan x}$
- $f(x) = \sin \left(\dfrac{x - \pi}{2}\right)$
- $f(x) = (2-x)^{10}$
VASTAUS
- $u(x) = \dfrac{1}{x}$ ja $s(x) = \tan x$
- $u(x) = \sin x$ ja $s(x) = \dfrac{x - \pi}{2}$
- $u(x) = x^{10}$ ja $s(x) = 2-x$
Yhdistetty funktio
Merkitään $f(x) = kx + 1$ ja $g(x) = 3x + k$. Määritä ne vakion $k$ arvot, joilla $$ (f\circ g)(x) = (g \circ f)(x). $$
VASTAUS
Yhtälö toteutuu, jos ja vain jos $k = -1$ tai $k = 2$.
Yhdistetty funktio
Muodosta yhdistetty funktio $g \circ f$, jos
- $f(x) = 2x - 1$ ja $g(x) = \dfrac{x+1}{2}$
- $f(x) = 4x + 3$ ja $g(x) = 0{,}25x - 0{,}75$.
Mitä huomaat?
Piirrä funktioiden $f$ ja $g$ kuvaajat samaan koordinaatistoon ja vertaa niitä suoraan $y = x$.
VASTAUS
- $(g\circ f)(x) = g(f(x)) = x$
- $(g\circ f)(x) = g(f(x)) = x$
Yhdistetyssä funktiossa funktiot $f$ ja $g$ kumoavat toistensa vaikutuksen ja tuloksena on sama muuttujan arvo, joka funktiolle alunperin syötettiin.
Sekä a- että b-kohdassa funktioiden $f$ ja $g$ kuvaajat ovat toistensa peilikuvia suoran $y = x$ suhteen.
Yhdistetty funktio
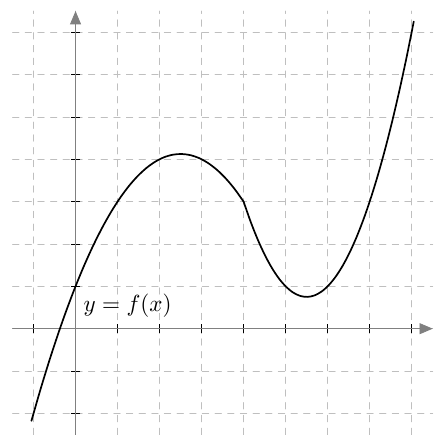
Määritä alla olevien kuvaajien avulla seuraavat yhdistetyn funktion $g \circ f$ arvot:
- $(g \circ f)(0)$
- $(g \circ f)(2)$
- $(g \circ f)(4)$
- $(g \circ f)(6)$
Kuvissa ruudukon ruudun sivun pituus on 1.
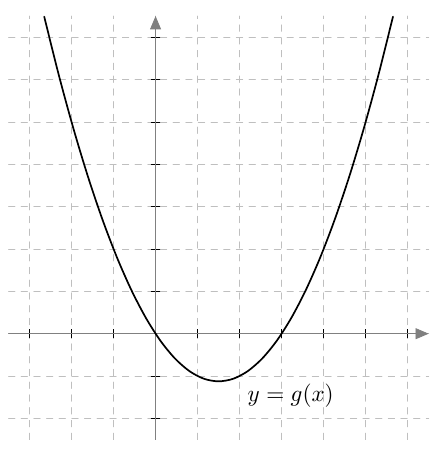
VASTAUS
- $g(f(0)) = g(1) = -1$
- $g(f(2)) = g(4) = 2$
- $g(f(4)) = g(3) = 0$
- $g(f(6)) = g(1) = -1$
Yhdistetty funktio
Määritä alla olevien kuvaajien avulla seuraavat yhdistetyn funktion $f \circ g$ arvot:
- $(f \circ g)(-2)$
- $(f \circ g)(0)$
- $(f \circ g)(1)$
- $(f \circ g)(4)$
Kuvissa ruudukon ruudun sivun pituus on 1.


VASTAUS
- $f(g(-2)) = f(5) = 1$
- $f(g(0)) = f(0) = 1$
- $f(g(1)) = f(-1) = -2$
- $f(g(4)) = f(2) = 4$
Yhdistetty funktio
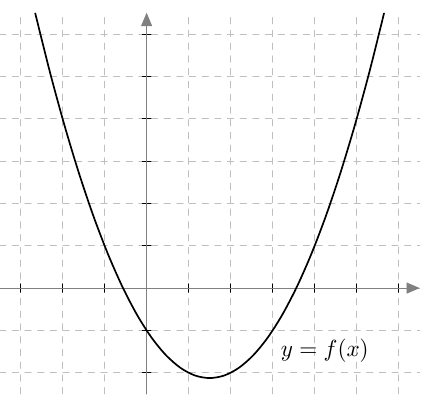
Alla on näkyvissä funktion $f$ kuvaaja. Hahmottele yhdistetyn funktion $g \circ f$ kuvaaja, jos
- $g(x) = -x$
- $g(x) = x + 3$
- $g(x) = \left|x\right|$
VASTAUS
- Kerroin $-1$ muuttaa funktion $f$ arvot vastaluvuikseen:
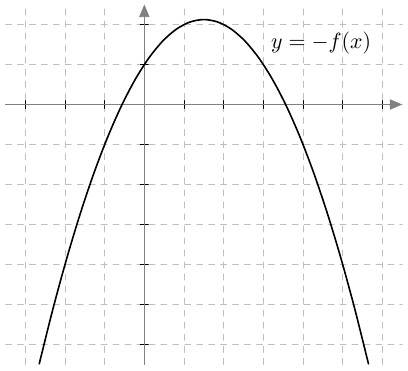
- Vakion lisääminen siirtää funktion $f$ kuvaajaa $y$-akselin suunnassa:
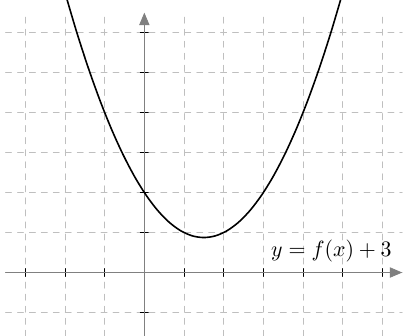
- Itseisarvo muuttaa funktion $f$ negatiiviset arvot vastaluvuikseen:
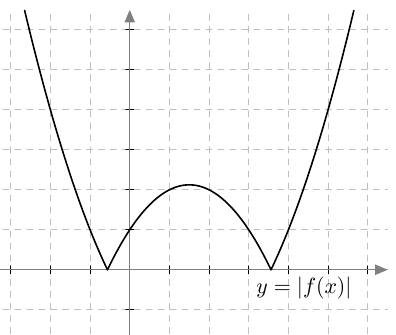
Yhdistetty funktio
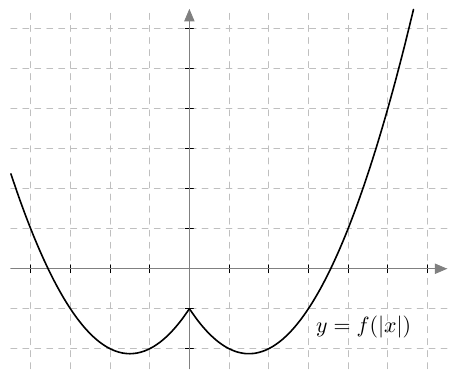
Alla on näkyvissä funktion $f$ kuvaaja. Hahmottele yhdistetyn funktion $f \circ s$ kuvaaja, jos sisäfunktio on
- $s(x) = -x$
- $s(x) = x - 1$
- $s(x) = \left|x\right|$

VASTAUS
- Sisäfunktion kerroin $-1$ peilaa funktion kuvaajan $y$-akselin suhteen:
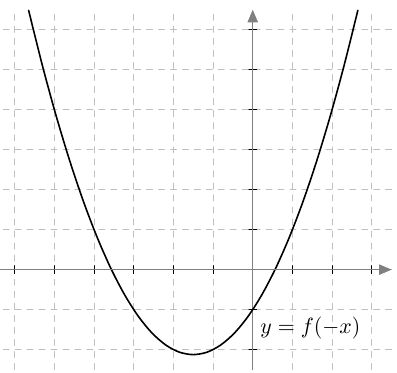
- Vakio sisäfunktiossa siirtää kuvaajaa $x$-akselin suunnassa:
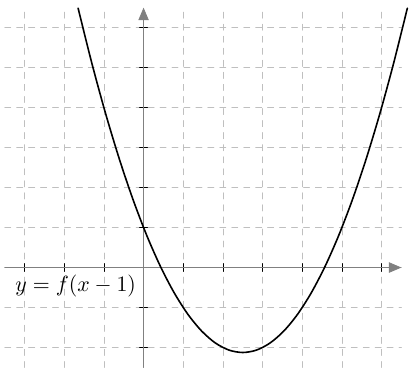
- Itseisarvo sisäfunktiossa tekee kuvaajasta symmetrisen $y$-akselin suhteen:
Yhdistetyn funktion derivaatta
Määritä funktion $f$ derivaattafunktio, jos
- $f(x) = \left(\dfrac{x}{x+1}\right)^3$
- $f(x) = \cos x^2$
VASTAUS
- $f'(x) = \dfrac{3x^2}{(x+1)^4}$
- $f'(x) = -2x\sin x^2$
Yhdistetyn funktion derivaatta
Tutkitaan funktion $f(x) = \sin 2x$ derivaattafunktiota.
- Määritä derivaattafunktio $f'(x)$ yhdistetyn funktion derivointisäännön avulla.
- Muokkaa funktion $f$ lauseketta kaksinkertaisen kulman kaavan avulla. Määritä sen jälkeen derivaattafunktio $f'(x)$ tulon derivointisäännön avulla.
Vinkki: kaksinkertaisen kulman kaava löytyy edellisestä luvusta teoreemasta 17 ja tulon derivointisääntö puolestaan MAA6-kurssin teoreemasta 13. - Vertaa a- ja b-kohdan tuloksia. Ovatko ne samat?
- Mille kaavalle saat uuden perustelun a- ja b-kohtien avulla?
VASTAUS
- $f'(x) = 2\cos 2x$
- $f(x) = 2\sin x\cos x$, joten derivaattafunktioksi saadaan $f'(x) = 2\cos^2\! x - 2\sin^2\! x$.
- Tulokset ovat samat, koska kysymyksessä on funktion $f$ derivaattafunktio vain eri tavoin määritettynä.
- Saadaan yhtälö $$ 2\cos 2x = 2\cos^2\! x - 2\sin^2\! x, $$ josta seuraa kaksinkertaisen kulman kosinin kaava $$ \cos 2x = \cos^2\! x - \sin^2\! x. $$
Yhdistetyn funktion derivaatta
Osoita, että funktio $f$ on kaikkialla aidosti kasvava, jos
- $f(x) = x + \sin x\cos x$
- $f(x) = 3x + \sin 2x - 4\sin x$
Vinkki: Kertaa tarvittaessa MAA6-kurssin teoreema 10. Kohdassa (b) myös tämän kurssin teoreemoista 7 ja 17 on apua.
VASTAUS
- Derivaattafunktio on \begin{align*} f'(x) &= 1 - \sin^2\! x + \cos^2\! x \\ &= \cos^2\! x + \cos^2\! x \\ &= 2\cos^2\! x. \end{align*} Havaitaan, että sen arvot ovat epänegatiiviset ja se saa arvon nolla vain yksittäisissä kohdissa. (Huomaa lyhennysmerkintä: $\cos^2\! x = (\cos x)^2$.)
- Derivaattafunktio on \begin{align*} f'(x) &= 3 + 2\cos 2x - 4\cos x \\ &= 3 + 2(\cos^2\! x - \sin^2\! x) - 4\cos x \\ &= 3 + 2\cos^2\! x - 2(1 -\cos^2\! x) - 4\cos x \\ &= 3 + 2\cos^2\! x - 2 + 2\cos^2\! x - 4\cos x \\ &= 4\cos^2\! x - 4\cos x + 1 \\ &= (2\cos\! x - 1)^2 \end{align*} Havaitaan, että sen arvot ovat epänegatiiviset ja se saa arvon nolla vain yksittäisissä kohdissa.
Yhdistetyn funktion derivaatta
Määritä funktion $f(x) = x - \sin 2x$ derivaattafunktion nollakohdat.
VASTAUS
Derivaattafunktio on $$f'(x) = 1 - 2\cos 2x.$$ Sen nollakohdat ovat $$\dfrac{\pi}{6} + n\cdot \pi$$ ja $$- \dfrac{\pi}{6} + n\cdot \pi,$$ missä $n$ on kokonaisluku.
Yhdistetyn funktion derivaatta
Derivoi funktio $f$, jos
- $f(x) = \cos^2 3x$
- $f(x) = \sin \dfrac{x}{2}$
VASTAUS
- $f'(x) = -6\cos 3x \sin 3x$
- $f'(x) = \dfrac{1}{2}\cos \dfrac{x}{2}$
Yhdistetyn funktion derivaatta
Pisteeseen, jossa funktion $$ f(x) = 2\tan x + \sin 6x - 4\cos x $$ kuvaaja leikkaa $y$-akselin, piirretään kuvaajan tangetti ja normaali. Määritä tangetin ja normaali yhtälöt.
Vinkki: kertaa tarvittaessa MAA3-kurssin teoreema 11.
VASTAUS
Tangentin yhtälö on $y = 8x - 4$. Normaalin yhtälö on $$ y = -\frac{1}{8}x - 4. $$
Yhdistetyn funktion derivaatta
Tarkastellaan funktiota $$ f(x) = a \sin x + b \cos 2x. $$ Määritä vakioiden $a$ ja $b$ arvot niin, että funktio $f$ toteuttaa ehdot $$ f\left(\frac{\pi}{6}\right) = 1 $$ ja $$ f''\left(\frac{\pi}{6}\right) = 1. $$ Vinkki: huomaa, että jälkimmäinen ehto koskee funktion $f$ toista derivaattaa, joka löydetään derivoimalla derivaattafunktio.
VASTAUS
$a = \dfrac{10}{3}$ ja $b = -\dfrac{4}{3}$
Yhdistetyn funktion derivaatta
Merkitään $$ f(x) = 4\cos 2x - 3\sin^2\! x. $$ Laske $$ f'\left(\frac{2\pi}{3}\right). $$
VASTAUS
Yhdistetyn funktion derivaatta
Määritä funktion $$ f(x) = (3x-7)\sin 3x + \cos 3x $$ suurin ja pienin arvo välillä $[0, \pi]$.
Vinkki: kertaa tarvittaessa MAA6-kurssin teoreema 12.
Vastaus
Suurin arvo on $$ f\left(\frac{\pi}{2}\right) = 7 - \frac{3\pi}{2}. $$ Pienin arvo on $$ f\left(\frac{\pi}{6}\right) = \frac{\pi}{2} - 7. $$
Yhdistetyn funktion derivaatta
Määritä kaikki funktion $$ f(x) = \cos \left(\frac{1-x}{x}\right) $$ derivaattafunktion nollakohdat.
Vastaus
$x = \dfrac{1}{1 + n\pi}$, missä $n$ on kokonaisluku.
TEHTÄVÄSARJA III
- Laske funktion $f(x) = \sin 3x$ derivaatan tarkka arvo kohdassa $x = \frac{\pi}{9}$
- Määritä ne reaaliluvut $x$, joilla funktion $f(x) = \cos\left(\frac{\pi}{2} - x\right)$ derivaatta on $\sin x$.
[Pitkä K2013/2a & S1999/4a]
Vastaus
- $f'\left(\frac{\pi}{9}\right) = 3\cos \frac{\pi}{3} = \frac{3}{2}$
- $x = \dfrac{\pi}{4} + n \cdot \pi$, missä $n$ on kokonaisluku
Määritä funktion $$ f(x) = \cos x - \frac{1}{2}\cos 2x $$ suurin ja pienin arvo. Missä pisteissä suurin arvo saavutetaan?
[Pitkä S2010/7]
Vastaus
Derivaattafunktion nollakohdat ovat $x = n \cdot \pi$ ja $$ x = \pm\frac{\pi}{3} + n \cdot 2\pi, $$ missä $n$ on kokonaisluku. Funktion suurin arvo on $\frac{3}{4}$ ja se saavutetaan kohdissa $$ x = \pm\frac{\pi}{3} + n \cdot 2\pi, $$ missä $n$ on kokonaisluku. Pienin arvo on $-\frac{3}{2}$.
Määritä funktion $$ f(x) = \frac{5}{4 + 3\cos 2x} $$ suurin ja pienin arvo reaalilukujen joukossa. Millä argumentin arvoilla nämä saadaan?
[Pitkä K2001/6]
Vastaus
Suurin arvo on $5$ ja se saavutetaan kohdissa $\frac{\pi}{2} + n \cdot \pi$, missä $n$ on kokonaisluku.
Pienin arvo on $\frac{5}{7}$ ja se saavutetaan kohdissa $n \cdot \pi$, missä $n$ on kokonaisluku.
Huom. tehtävän voi ratkaista myös päättelemällä ilman derivaattaa, koska tiedetään, että kosinin arvot ovat aina välillä $[-1,1]$.
Puistossa on kaksi toisiaan vastaan kohtisuoraa käytävää sekä koirien suosima puu, jonka etäisyys toisesta käytävästä on 60 m, toisesta 100 m. Käytävien väliin on muodostunut lyhin mahdollinen suora oikopolku, joka sivuaa puuta. Minkä kulman tämä oikopolku muodostaa puuta lähempänä olevan käytävän kanssa? Anna vastaus kahden merkitsevän numeron tarkkuudella.
[Pitkä S1990/8b]
Vastaus
Polun pituus saadaan funktiosta $$ f(x) = \frac{60}{\sin x} + \frac{100}{\cos x}, $$ missä $x$ on kysytty kulma (välillä $\left[0, \frac{\pi}{2}\right]$). Derivaattafunktio on \begin{align*} f'(x) &= \frac{5\sin x}{\cos^2\! x} - \frac{3\cos x}{\sin^2\! x}. \end{align*} Sen nollakohdat löydetään ratkaisemalla yhtälö $$ \frac{\sin^3\! x}{\cos^3\! x} = \frac{3}{5} $$ eli yhtälö $$ \tan^3\! x = \frac{3}{5}. $$ Välillä $\left[0, \frac{\pi}{2}\right]$ on yksi nollakohta $x \approx 0{,}70$ (radiaania). Kulkukaavion avulla havaitaan, että tämä on minimikohta. Kysytty kulma on siis noin 40 astetta.
Määritä funktion $$ f(x) = (1-\cos^3\!x)^3 $$ suurin ja pienin arvo
- päättelemällä kosinin ominaisuuksien avulla
- derivaatan avulla.
Vastaus
Suurin arvo on 8 ja pienin arvo on 0.
- Idea: Kosinin saa arvot välillä $[-1,1]$, joten $1 - \cos^3\! x$ saa arvot välillä $[0, 2]$. Kysytty suurin arvo on siten $2^3 = 8$ ja pienin arvo on $0$.
- Derivaattafunktio on $$ f'(x) = 3(1-\cos^3\!x)^2 \cdot (-3\cos^2\! x) \cdot (-\sin x). $$ Sillä on nollakohdat $n \cdot \pi$ ja $$ \frac{\pi}{2} + n \cdot \pi, $$ missä $n$ on kokonaisluku.
Funktion $f$ arvot toistuvat $2\pi$:n jaksoissa, joten suurin ja pienin arvo löydetään laskemalla funktion arvot kohdissa $x = 0$, $x = \frac{\pi}{2}$, $x = \pi$ ja $x = \frac{3\pi}{2}$.
Kourua pitkin valuu $0{,}2 \text{ m}^3/\text{min }$ seulottua hiekkaa ympyräpohjaisen kartion muotoiseen kasaan. Hiekkakasan korkeuden kasvaessa myös pohjaympyrän halkaisija $d$ kasvaa niin, että se on koko ajan 50 % kasan korkeutta suurempi. Tehtävänä on selvittää, millä nopeudella hiekkakasan korkeus kasvaa hetkellä, jolloin sen korkeus on 1,5 metriä.
- Piirrä tilanteesta mallikuva ja muodosta yhtälö, joka kertoo, miten pohjaympyrän halkaisija $d$ riippuu kasan korkeudesta $h$.
- Muodosta yhtälö ympyräpohjaisen kartion tilavuudelle ja muokkaa sitä niin, että siinä esiintyy vain tilavuus $V$, korkeus $h$ sekä vakioita.
Vinkki: kertaa tarvittaessa MAA3-kurssin teoreema 25. - Hiekkakasan tilavuus ja korkeus riippuvat kumpikin ajasta eli ne ovat ajan funktioita $V(t)$ ja $h(t)$. Derivoimalla b-kohdassa johtamasi tilavuuden lausekkeen saat lausekkeen tilavuuden muutosnopeudelle $V'(t)$.
Vinkki: Nyt tarvitset yhdistetyn funktion derivointisääntöä (teoreema 23). - Selvitä c-kohdan yhtälön avulla, millä nopeudella hiekkakasan korkeus kasvaa hetkellä, jolloin sen korkeus on 1,5 metriä.
Vastaus
- $d = 1{,}5h$
- $V = \dfrac{3\pi h^3}{16}$
- $V'(t) = \dfrac{3\pi \cdot 3 (h(t))^2 \cdot h'(t)}{16}$
- \begin{align*} h'(t) &= \dfrac{16V'(t)}{9\pi (h(t))^2} \\[2mm] &= \dfrac{16 \cdot 0{,}2 \text{ m}^3/\text{min}}{9\pi \cdot (1{,}5 \text{ m})^2} \\[2mm] &\approx 0{,}050 \text{ m/min} \end{align*}
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

