MAY1 - Luvut ja yhtälöt
Moduulin tavoitteet ja keskeiset sisällöt
Matematiikan asema aikamme kulttuurissa edellyttää valmiutta ymmärtää, hyödyntää ja tuottaa matemaattisesti esitettyä tietoa. Sillä on merkittävä tai ratkaiseva rooli muun muassa tieteissä, teknologiassa, taloudessa, yrittäjyydessä, terveydenhuollossa ja turvallisuudessa. Matematiikan opiskelun tehtävänä on tutustuttaa sinut matemaattisen ajattelun malleihin sekä matematiikan perusideoihin ja rakenteisiin, opettaa sinua käyttämään puhuttua ja kirjoitettua matematiikan kieltä sekä kehittää laskemisen, ilmiöiden mallintamisen ja ongelmien ratkaisemisen taitojasi.
Syksystä 2016 lukion matematiikan opiskelu alkaa pitkän ja lyhyen oppimäärän yhteisellä moduulilla. Matematiikan yhteinen moduuli avaa näköaloja matematiikan moninaiseen merkitykseen ihmiselle ja yhteiskunnalle sekä sen ainutlaatuiseen ja kiehtovaan olemukseen tieteenalana. Tässä moduulissa sinulla on tilaisuus vahvistaa pohjaa matematiikan opinnoillesi ja nähdä matematiikka hyödyllisenä ja käyttökelpoisena selitettäessä ja hallittaessa muun muassa yhteiskunnan, talouden ja luonnon tapahtumia ja tilanteita.
Moduulin tavoitteena on, että
- kertaat prosenttilaskennan periaatteet
- osaat käyttää verrannollisuutta ongelmanratkaisussa
- syvennät murtolukujen laskutoimitusten osaamistasi
- kertaat potenssin laskusäännöt
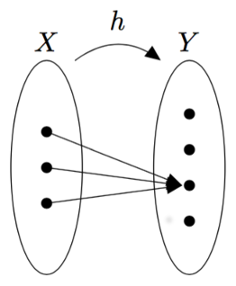
- vahvistat ymmärrystäsi funktion käsitteestä
- ymmärrät yhtälön ja yhtälöparin ratkaisemisen periaatteet
- opit käyttämään ohjelmistoja funktion kuvaajan piirtämisessä, havainnoinnissa ja yhtälöiden ratkaisemisessa.
Keskeiset sisällöt
- lukujoukot ja peruslaskutoimitukset
- luvun vastaluku, käänteisluku ja itseisarvo
- prosenttilaskenta
- potenssin laskusäännöt (eksponenttina kokonaisluku)
- suoraan ja kääntäen verrannollisuus
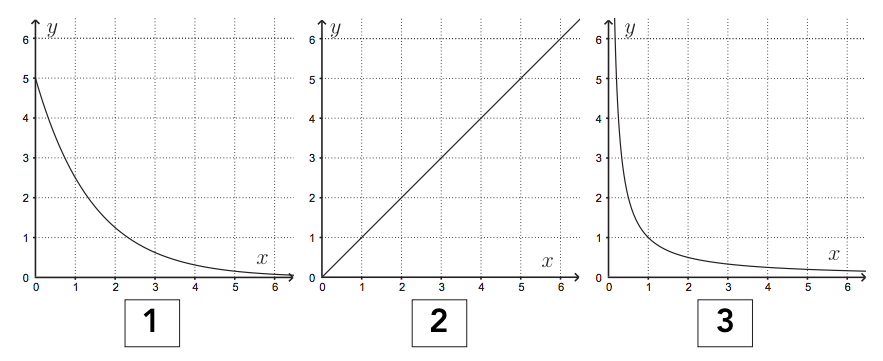
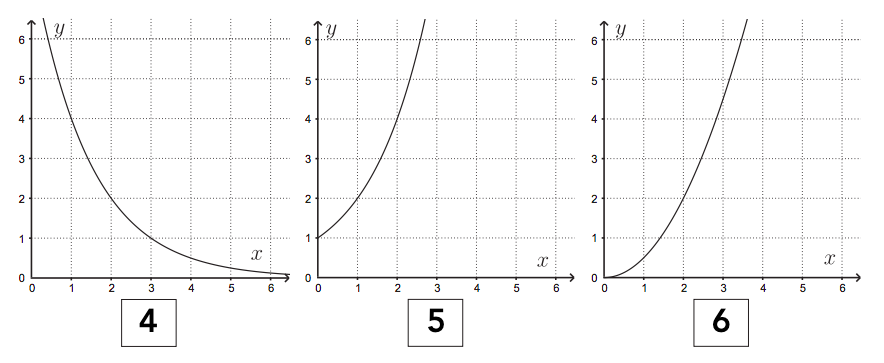
- funktio, kuvaajan piirto ja kuvaajan tulkinta
- ensimmäisen asteen yhtälön ratkaiseminen
- yhtälöpari
- neliö- ja kuutiojuuri
- potenssifunktio ja potenssiyhtälö (asteluvut 2 ja 3)
Opiskeluohjeita
Kurssimateriaali on jaettu viiteen lukuun: Luvut ja laskutoimitukset, Potenssi, Funktiot ja yhtälöt, Yhtälöpari ja verrannollisuus sekä Prosenttilaskenta.
Pääajatus kurssimateriaalissa on, että matematiikkaa oppii parhaiten tekemällä matematiikkaa. Näin ollen se on kirjoitettu niin, että teet tehtäviä käytännössä koko ajan. Jokainen luku sisältää kolme eri tehtäväsarjaa. Ensimmäisen tehtäväsarjan tehtävät ovat teorian seassa. Tarkoitus on, että etenet materiaalissa tekemällä jokaisen näistä tehtävistä. Voit hyvin tehdä tehtäviä yhdessä kaverin kanssa ja voit kysyä opettajalta heti, jos et ymmärrä jotain asiaa. Asia voi olla jokin tietty tehtävä, teoriassa oleva virke tai esimerkiksi vieras matemaattinen symboli. Pääasia on, että sinä itse teet tehtävät ja ymmärrät, mitä teet. Tämän tehtäväsarjan jälkeen kyseisen luvun teoria on käsitelty ja on aika harjoitella ja syventää juuri opittua. Ennen tätä opettaja pitää ehkä yhteisen opetustuokion tai -keskustelun, jossa pohditaan yhdessä luvun keskeisiä asioita tai työskentelyssä esiin tulleita haastavia kohtia. Mahdollisen opetustuokion jälkeen jatka harjoittelua luvun lopussa olevien kahden tehtäväsarjan tehtävien avulla. Luonnollisesti mitä enemmän harjoittelet, sitä paremmaksi tulet. Kun olet valmis, tee luvun lopussa oleva(t) itsearviointitesti(t). Niiden tarkoitus on kertoa sinulle, oletko ymmärtänyt luvun olennaiset asiat ja kehittää samalla oman oppimisesi arviointia, joka on tärkeä tulevaisuuden taito. Testeissä pärjääminen ei vielä tarkoita, että osaat luvun asiat esimerkiksi kiitettävällä tasolla, vaan testit keskittyvät vahvan perusosaamisen tutkimiseen. Ennen siirtymistä seuraavaan lukuun opettaja haluaa ehkä vielä koota luvussa opittuja asioita sekä antaa palautetta oppimisesta ja sen etenemisestä yhteisessä opetuskeskustelussa.
Matematiikan merkityksestä yhteiskunnalle ja yksilölle
Olet opiskellut matematiikkaa koko perusopetuksen ajan, joten nyt lukion matematiikan opiskelun alussa on hyvä hetki pohtia, miksi sitä opiskellaan. Oletkin saattanut pohtia sitä ystäväsi, opettajasi tai vanhempiesi kanssa. Kysymys on saattanut liittyä johonkin tiettyyn matematiikan tunneilla käsiteltyyn aiheeseen tai koko oppiaineeseen. En tiedä, mihin johtopäätökseen mahdollisesti tulit, mutta kuten hyvät kysymykset usein ovat, niihin voi olla vaikeaa vastata.
Voidaan tokki sanoa, että matematiikkaa opiskellaan, jotta sitä voitaisiin soveltaa jossakin ilmeisessä arkisessa toiminnassa kuten kaupankäynnissä, tilastojen tekemisessä tai fysikaalisten ilmiöiden mallintamisessa. Voidaan myös sanoa, että jotakin tiettyä matematiikan aihetta opiskellaan, koska sitä mahdollisesti tarvitaan tulevissa opinnoissa. Haastavaksi vastaamisen tekee se, että matematiikka sisältyy niin erottumattomana osana meidän yhteiskuntaamme ja kulttuuriimme, että emme aina oikein edes huomaa, miten sitä hyödynnetään ympärillämme. Eläimet eivät tarvitse matematiikkaa selvitäkseen hengissä, joten välttämätöntä ihmiskunnan selviämiselle matematiikka ei ole, mutta nykyisenkaltaiselle yhteiskunnalle matematiikka on elintärkeätä.
Tarkastellaan esimerkiksi lukuja. Tähtiteteen professori Tapani Markkanen on todennut, että
"lukukäsitteen synty on sekä ihmislajin että yksilön kannalta mullistavimpia edistysaskeleita."
Miksi luvut ovat Markkasen mielestä ihmiskunnalle niin tärkeitä?
Pohdi parin kanssa, minkälainen ihmiskunta olisi, jos se ei osaisi käsitellä lukumääriä luvuilla. Voisimmeko äänestää? Tietäisimmekö ikämme?
Edellisen tehtävän pohdinnan kautta ehkä huomaat, että matematiikkaa lukujen muodossa on ihmisten luomassa yhteiskunnassa kaikkialla. Vaikka päällisin puolin luvut vaikuttavatkin melko yksinkertaiselta ihmismielen keksinnöltä, niin matematiikan kehitys on vuosituhansien saatossa on puskenut ymmärrystämme lukujen moninaisuudesta eteenpäin.
Kokonaisluvut ovat hyviä lukumäärien laskemiseen, mutta kun halutaan verrata esimerkiksi lukumääriä toisiinsa, huomataan, etteivät ne pelkästään riitä. Esimerkiksi kuinka moninkertaisesti Ronaldo (35) teki maaleja verrattuna Messiin (26) La Ligassa kaudella 2015-2016? Tämän ratkaisemiseen tarvitaan matemaattisia keksintöjä, laskutoimituksia, ja vastaukseksi saatu luku $\frac{35}{26}$ on luku yhden ja kahden välissä, eli se ei ole kokonaisluku. Meidän yhteiskunnassamme murtoluvut ja niillä laskeminen opitaan perusopetuksessa, mutta ihmiskunnalle niiden kehittäminen on ollut suurten ponnistuksien ja oivalluksien tulos.
Murtolukujakin monimukaisempiin lukuihin olet myös törmännyt perusopetuskessa. Yläkoulun matematiikasta muistat ehkä Pythagoraan lauseen, joka sanoo, että suorakulmaisen kolmion kateettien pituuksien $a$ ja $b$ suhde hypotenuusan pituuteen $c$ on $$a^2 + b^2 = c^2.$$
Ehkä sinulle heräsi yläkoulussa kysymys, miksi tällaistakin pitäisi osata. Yksinkertainen vastaus olisi se, että sen avulla pystytään laskemaan erilaisten suorakulmaisten kolmioiden sivujen pituuksia. Tämä on merkittävä syy ja osoittaa Pythagoraan lauseen voiman, sillä se pätee kaikkiin suorakulmaisiin kolmioihin. Tämä on kuitenkin vain pintaraapaisu.
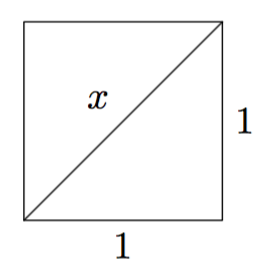
Yksi ihmismieltä askarruttanut arvaamaton tulos Pythagoraan lauseesta saadaan, kun laitetaan $a$:n ja $b$:n tilalle luku 1. Huomaat, että $c$ saa hyvin oudon arvon. Tämä arvo on esimerkki irrationaaliluvusta, luvusta joka ei ole murtoluku, eli sitä ei voi esittää kahden kokonaisluvun suhteena. Tämän antiikin kreikkalaiset pystyivät todistamaan, ja se saatetaan myös todistaa kurssissa MAA11. Kesti jokunen tuhat vuotta, kunnes äärettömyydestä ja äärettömistä joukoista ymmärrettiin matemaattisesti niin paljon, että 1800-luvulla pystyttiin todistamaan, että näitä irrationaalilukuja on tietyssä mielessä enemmän kuin rationaalilukuja. Kuten matematiikan professori Olli Martio on todennut:
"Muutaman tuhannen vuoden takaiset matematiikan tulokset, kuten suorakulmaista kolmiota koskeva Pythagoraan lause, muodostavat edelleen ihmiskunnan kulttuuriperinnön kivijalan."
Edellä puhuttiin todistamisesta. Pythagoraan lauseen tunsivat viimeistään pythagoralaiset noin 500 e.a.a., mutta mistä tiedämme, että se tosiaan pätee kaikille suorakulmaisille kolmioille? Pystymme todistamaan Pythagoraan lauseen todeksi ja olet ehkä nähnyt erilaisia todistuksia sille.
Olemme tottuneita hyödyntämään monia tosina pitämiämme matematiikan tuloksia. Ne erottaa mielipiteistä tai luuloista se, että ne voidaan todistaa paikkaansa pitäviksi. Todistaminen ei aina ole kovin yksinkertaista. Jos olet esimerkiksi alakoulussa oppinut jakamaan lukuja jakokulmassa, et todennäköisesti vielä ole nähnyt todistusta sille, että jakokulma todellakin toimii. Todistus vaatii tiedon jakoyhtälön totuudesta, jota tutkitaan esimerkiksi kurssilla MAA11 tai yliopiston ensimmäisillä algebran kursseilla.
Monia matemaattisia totuuksia ei olla vielä löydetty. Matemaatikot eri puolilla maailmaa työskentelevät paraikaa lukemattomien matemaattisten ongelmien parissa, etsien niiden totuutta. Yksi maailman tunnetuimmista matemaattisista ongelmista oli, onko olemassa positiiviset kokonaisluvut $a$, $b$ ja $c$, jotka toteuttavat Pythagoraan lauseen yhtälöä muistuttavan yhtälön $$a^n + b^n = c^n,$$
jos $n$ on lukua 2 suurempi luonnollinen luku. Kysymyksen esitti antiikin kreikkalainen matemaatikko Diofantos ja ranskalainen matemaatikko Pierre Fermat kirjoitti 1600-luvulla löytäneensä vastauksen. Hänen vastaustaan ei kuitenkaan koskaan löydetty.
Kului yli 300 vuotta ja useiden aikansa nerokkaimpien matemaatikoiden yrityksiä kunnes brittiläinen matemaatikko Andrew Wiles selvitti tämän Fermat'n suureksi lauseeksi kutsutun ongelman. Vastaus on, että sellaista lukua $n$ ei ole olemassa. Tämän selvittämiseksi Wiles joutui kehittämään runsaasti uutta matemaattista teoriaa.
Ratkaisematon ongelma
Etsi yksi matemaattinen ongelma, jota ihmiskunta ei vielä ole pystynyt ratkaisemaan. Sinun ei tarvitse kokonaan ymmärtää mistä ongelmassa on kyse, mutta yritä selittää se ystävällesi niin hyvin kuin pystyt.
Vinkki
Laita hakukoneeseen “Luettelo ratkaisemattomista matemaattisista ongelmista”.
Sinulle on ehkä kerrottu, että matematiikan opiskelu harjaannuttaa ajattelun taitoa. Tämä ei luonnollisesti ole matematiikan erityisoikeus, vaan eri oppiaineet harjaannuttavat erilaisia ajattelun taitoja. Kuten yllä on pohdittu, voidaan kuitenkin sanoa, että ihmiskunnan kehityksen kannalta matemaattisen ajattelun merkitys on ollut merkittävä.
Matematiikka on aikojen saatossa kehittynyt monitahoiseksi tieteeksi. Kansainvälisessä luokittelussa matematiikka on jaettu noin 50 pääryhmään ja nämä edelleen aliryhmiin. Kussakin näistä on omat avoimet ongelmansa, joita matemaatikot ympäri maailmaa yrittävät ratkaista. Esimerkiksi algebra tutkii laskutoimituksia, geometria ja logiikka todistamista sekä matematiikan perusteita.
Akateemikko Olli Lehto on todennut:
"Pohjimmaltaan paljolti matematiikkaan perustuva luonnontieteellis-teknologinen tieto on edellytyksenä menestymiseen taloudellisessa kilpailussa, se on pohjana yhteiskuntaa ohjaaville poliittisille päätöksille, ja sitä tarvitaan kestävän kehityksen turvaamisessa."
Kuka tietää mikä matematiikan ja matemaattisen ajattelun muoto seuraavaksi mullistaa yhteiskuntaamme!





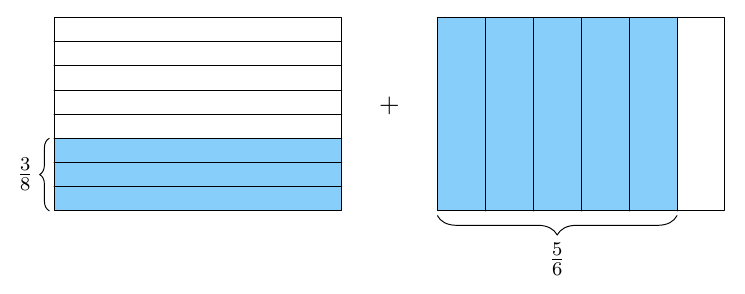
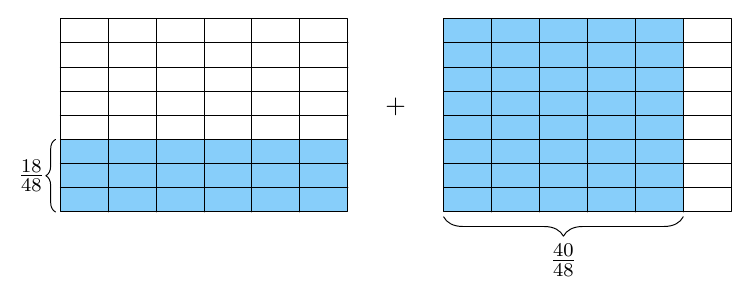
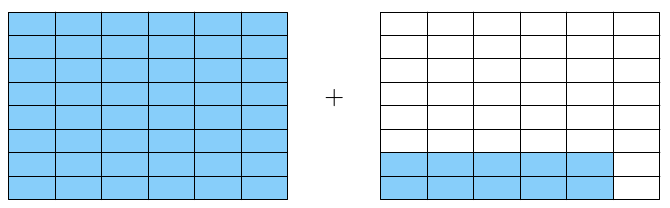
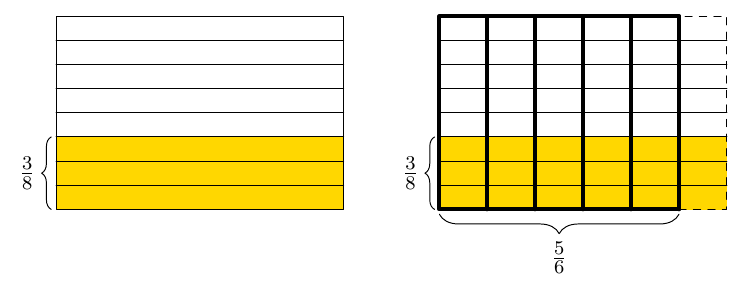
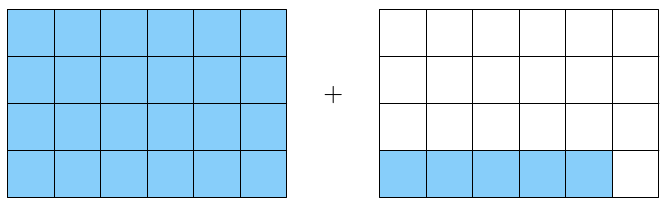 Tulos voidaan siis ilmoittaa supistetussa muodossa \begin{align*} \dfrac{3}{8} + \frac{5}{6} &= \dfrac{58}{48} \\[2mm] &=\dfrac{2\cdot 29}{2 \cdot 24} \\[2mm] &=\dfrac{29}{24} \end{align*} Luku $29$ ei ole jaollinen millään ykköstä suuremmalla luvulla paitsi itsellään, joten supistamista ei voi jatkaa tämän pidemmälle.
Tulos voidaan siis ilmoittaa supistetussa muodossa \begin{align*} \dfrac{3}{8} + \frac{5}{6} &= \dfrac{58}{48} \\[2mm] &=\dfrac{2\cdot 29}{2 \cdot 24} \\[2mm] &=\dfrac{29}{24} \end{align*} Luku $29$ ei ole jaollinen millään ykköstä suuremmalla luvulla paitsi itsellään, joten supistamista ei voi jatkaa tämän pidemmälle. 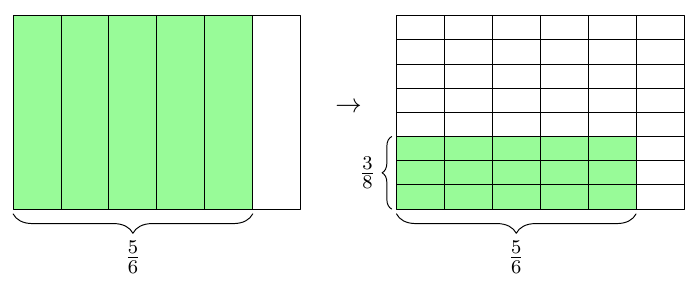
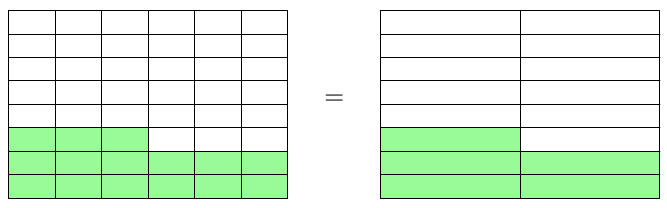
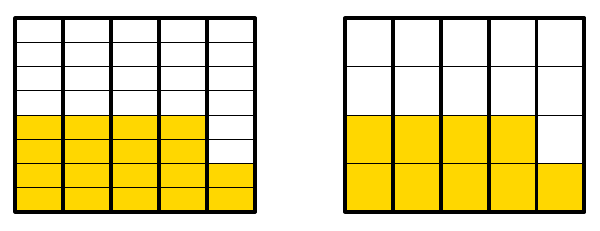
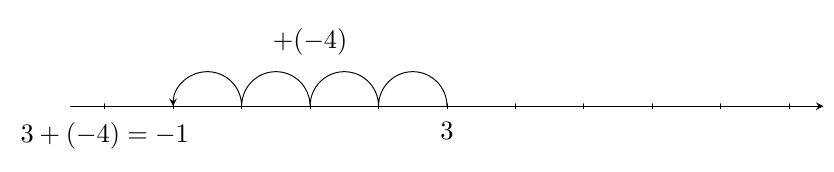
 Laskutoimitusta $5 : 2$ voidaan havainnollistaa kahdella tavalla:
Laskutoimitusta $5 : 2$ voidaan havainnollistaa kahdella tavalla: