Funktio
Luvun tavoitteet
Tämän luvun tavoitteena on, että tunnet funktion käsitteen ja osaat piirtää ja tulkita funktioiden kuvaajia. Osaat
- tunnistaa, onko sääntö funktio, ja päätellä, mikä on funktion määrittelyehto
- määrittää funktion arvon tietyssä kohdassa kuvaajasta päättelemällä, käsin laskemalla ja laskimen avulla
- lukea kuvaajasta funktion nollakohdat sekä sen, missä funktion arvot ovat positiivisia ja missä negatiivisia
- piirtää laskimella funktion kuvaajan
- tunnistaa ensimmäisen asteen polynomifunktion kuvaajan ominaisuuksia funktion lausekkeesta
- tunnistaa eksponentti- ja logartimifunktioiden kuvaajat.
Funktio
Tässä luvussa tutustutaan funktion käsitteeseen. Sen avulla voidaan mallintaa ja tutkia erilaisten mitattavissa olevien asioiden välisiä riippuvuuksia, kuten esimerkiksi pyöräilijän tiettynä aikana kulkeman matkan riippuvuutta pyöräilijän vauhdista tai työntekijän maksamien verojen määrän riippuvuutta työntekijän tuloista.
Funktio on siis jonkinlainen sääntö, joka kertoo, miten jokin asia liittyy toiseen. Ennen kuin sovimme tarkemmin, mitä funktion käsitteellä tarkoitetaan, tutkitaan seuraavissa tehtävissä muutamien erilaisten sääntöjen ominaisuuksia.
Erilaisia sääntöjä
Tutkitaan sääntöä $f$, joka liittää jokaiseen luonnolliseen lukuun sen numeroiden summan. Siis esimerkiksi lukuun $156$ sääntö $f$ liittää luvun $1 + 5 + 6 = 12$. Tämä voidaan merkitä $$f(156) = 1 + 5 + 6 = 12.$$
- Minkä luvun sääntö $f$ liittää lukuun $389$? Toisin sanottuna, mikä on $f(389)$?
- Minkä luvun sääntö $f$ liittää lukuun $106\,437$? Toisin sanottuna, mikä on $f(106\,437)$?
- Onko olemassa jokin luonnollinen luku, jonka tapauksessa säännön $f$ antamaa tulosta ei voida laskea? Selitä omin sanoin.
- Onko olemassa jokin luonnollinen luku, johon sääntö $f$ liittää useita eri lukuja? Selitä omin sanoin.
VASTAUS
- $f(389) = 3 + 8 + 9 = 20$
- $f(106\,437) = 21$
- Tällaista lukua ei ole olemassa, sillä luvun numeroiden summa voidaan aina laskea.
- Tällaista lukua ei ole olemassa, sillä olipa alkuperäinen luku mikä tahansa, sen numeroiden summasta tulee aina yksi tulos.
Erilaisia sääntöjä
Tutkitaan sääntöä $g$, joka liittää jokaiseen kaksinumeroiseen luonnolliseen lukuun sen numeroiden erotuksen käänteisluvun. Siis esimerkiksi lukuun $36$ sääntö $g$ liittää luvun $$\frac{1}{3-6} = \frac{1}{-3} = -\frac{1}{3}.$$ Tämä voidaan merkitä $$g\left(36\right) = \frac{1}{3-6} = -\frac{1}{3}.$$
- Minkä luvun sääntö $g$ liittää lukuun $94$? Toisin sanottuna, mikä on $g(94)$?
- Minkä luvun sääntö $g$ liittää lukuun $77$? Toisin sanottuna, mikä on $g(77)$?
- Onko olemassa jokin kaksinumeroinen luonnollinen luku, jonka tapauksessa säännön $g$ antamaa tulosta ei voida laskea? Selitä omin sanoin.
- Onko olemassa jokin kaksinumeroinen luonnollinen luku, johon sääntö $g$ liittää useita eri lukuja? Selitä omin sanoin.
VASTAUS
- $g(94) = \dfrac{1}{9-4} = \dfrac{1}{5}$
- $g(77)$ ei ole määritelty, sillä murtoluvun nimittäjäksi tulisi nolla eikä nollalla jakamista ole määritelty.
- Esimerkiksi 77.
- Tällaista lukua ei ole olemassa, sillä jos tulos voidaan laskea, se on aina jokin tietty luku.
Erilaisia sääntöjä
Tutkitaan sääntöä $h$, joka liittää jokaiseen murtolukumuodossa kirjoitettuun rationaalilukuun sen osoittajan ja nimittäjän summan. Siis esimerkiksi lukuun $\frac{42}{105}$ sääntö $h$ liittää luvun $42 + 105 = 147$. Tämä voidaan merkitä $$h\left(\frac{42}{105}\right) = 42 + 105 = 147.$$
- Minkä luvun sääntö $h$ liittää lukuun $\frac{2}{4}$? Toisin sanottuna, mikä on $h\left(\frac{2}{4}\right)$?
- Minkä luvun sääntö $h$ liittää lukuun $\frac{1}{2}$? Toisin sanottuna, mikä on $h\left(\frac{1}{2}\right)$?
- Onko olemassa jokin rationaaliluku, jonka tapauksessa säännön $h$ antamaa tulosta ei voida laskea? Selitä omin sanoin.
- Onko olemassa jokin rationaaliluku, johon sääntö $h$ liittää useita eri lukuja? Selitä omin sanoin.
VASTAUS
- $h\left(\frac{2}{4}\right) = 2 + 4 = 6$
- $h\left(\frac{1}{2}\right) = 1 + 2 = 3$
- Tällaista lukua ei ole olemassa, sillä olipa kysymyksessä mikä tahansa rationaaliluku, se voidaan kirjoittaa murtolukumuodossa ja laskea osoittajan ja nimittäjän summa.
- Esimerkiksi luku 0,5 voidaan kirjoittaa murtolukumuodossa eri tavoin: $0{,}5 = \frac{1}{2} = \frac{2}{4}$. Säännön $h$ antama tulos riippuu murtoluvun esitysmuodosta kuten kohdista (a) ja (b) nähdään.
Edellisissä tehtävissä tutkittiin erilaisia sääntöjä, jotka kaikki liittivät tietyn joukon lukuihin toisia lukuja. Sellaista sääntöä, joka liittää tietyn joukon jokaiseen alkioon täsmälleen yhden alkion, sanotaan funktioksi.
MÄÄRITELMÄ: FUNKTIO
Funktio joukosta $X$ joukkoon $Y$ tarkoittaa sääntöä, joka liittää joukon $X$ jokaiseen alkioon täsmälleen yhden alkion joukosta $Y$.
Tässä esiintyvä joukko $X$ on funktion määrittelyjoukko eli lähtöjoukko ja joukko $Y$ on funktion maalijoukko.
Funktio
Tarkastele vielä tehtävien 1-3 sääntöjä $f$, $g$ ja $h$.
- Onko sääntö $f$ funktio? Selitä omin sanoin.
- Onko sääntö $g$ funktio? Selitä omin sanoin.
- Onko sääntö $h$ funktio? Selitä omin sanoin.
- Valitse säännöistä $f$, $g$ ja $h$ yksi, joka on funktio. Mikä on sen määrittelyjoukko? Entä minkä lukujoukon voi valita sen maalijoukoksi? Keksi kaksi erilaista vaihtoehtoa maalijoukoksi.
VASTAUS
- Sääntö $f$ on funktio, sillä se liittää jokaiseen luonnolliseen lukuun täsmälleen yhden luonnollisen luvun.
- Sääntö $g$ ei ole funktio, sillä esimerkiksi lukuun 11 se ei liitä mitään.
- Sääntö $h$ ei ole funktio, sillä se liittää esimerkiksi lukuun $0{,}5$ eri lukuja riippuen siitä, millaisessa murtolukumuodossa luku $0{,}5$ esitetään.
- Funktion $f$ määrittelyjoukko on luonnollisten lukujen joukko. Maalijoukko voi olla luonnollisten lukujen joukko tai jokin laajempi lukujoukko, esimerkiksi kokonaislukujen tai reaalilukujen joukko.
Funktio
Tarkastele alla olevia kuvia, joissa on kuvattu säännöt $\alpha$, $f$, $g$, $\beta$ ja $h$. Mitkä näistä säännöistä ovat funktioita joukosta $X$ joukkoon $Y$? Perustele omin sanoin.
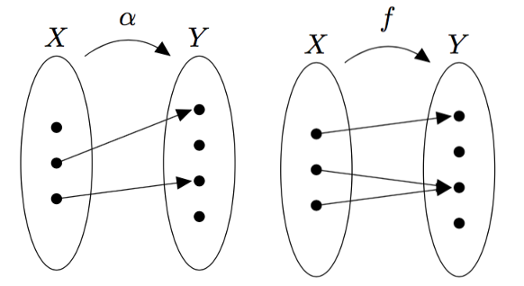
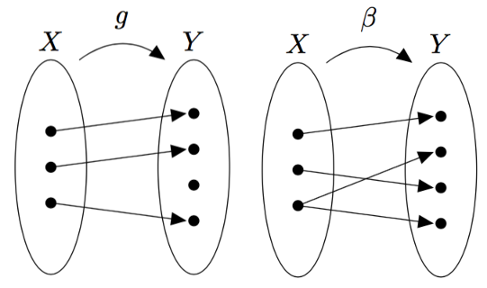
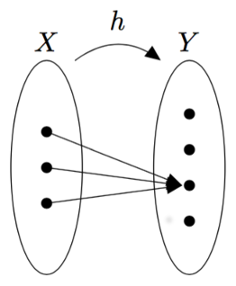
VASTAUS
Säännöt $f$, $g$ ja $h$ ovat funktioita joukosta $X$ joukkoon $Y$, sillä ne liittävät jokaiseen joukon $X$ alkioon täsmälleen yhden alkion joukosta $Y$.
Sääntö $\alpha$ ei ole funktio joukosta $X$ joukkoon $Y$, sillä joukossa $X$ on alkio, johon sääntö $\alpha$ ei liitä yhtään joukon $Y$ alkiota.
Sääntö $\beta$ ei ole funktio joukosta $X$ joukkoon $Y$, sillä joukossa $X$ on alkio, johon sääntö $\beta$ liittää useamman kuin yhden joukon $Y$ alkion.
Joskus funktion sääntö voidaan ilmaista lausekkeen avulla. Esimerkiksi merkintä $$f(x) = 2x + 1$$ ilmaisee sen, että funktio $f$ liittää lukuun $x$ luvun $2x + 1$. Funktio $f$ siis kertoo luvun $x$ kahdella ja lisää tulokseen luvun $1$.
Funktion arvon laskeminen
Tarkastellaan funktiota $h(x) = -x^2-3x+1$.
- Laske funktion $h$ arvo kohdassa $x = 2$. Toisin sanottuna laske, mitä on $h(2)$.
- Kaksi opiskelijaa laski funktion $h$ arvon kohdassa $x = -4$. Opiskelija A laski seuraavasti: \begin{align*} h(-4) &= --4^2-3\cdot -4 + 1 \\ &= +4^2 + 12 + 1 \\ &= 16 + 12 + 1 = 29. \end{align*} Opiskelija B puolestaan laski näin: \begin{align*} h(-4) &= -(-4)^2 - 3\cdot (-4) + 1 \\ &= -16+12 + 1 = -3. \end{align*} Kumman lasku oli oikein?
- Laske funktion $h$ arvo kohdassa $x = -\frac{1}{2}$.
VASTAUS
- $h(2) = -9$
- Opiskelijan B lasku oli oikein. Huomaa sulkujen vaikutus.
- $h\left(-\frac{1}{2}\right) = \frac{9}{4}$
Koordinaatiston pisteet
Piirrä vihkoosi samanlainen koordinaatisto kuin alla ja merkitse siihen pisteet $(2,-1)$, $(-3,0)$, $(5,2)$, $(-4,1)$, $(1,0)$, $(6,3)$, $(-5,2)$, $(0,1)$, $(3,0)$, $(-6,3)$, $(-2,-1)$, $(4,1)$ ja $(-1,0)$. Millainen kuvio koordinaatistoon syntyy?
Monia funktioita voidaan havainnollistaa piirtämällä funktion kuvaaja koordinaatistoon. Jotta kuvaaja voidaan piirtää, täytyy tietää, mitä arvoja funktio saa muuttujan eri arvoilla. Kuvaajaa piirrettäessä muuttujan arvot luetaan vaaka-akselilta ($x$-akselilta) ja funktion arvot pystyakselilta ($y$-akselilta).
Funktion arvon laskeminen ja funktion kuvaaja
Tutkitaan vielä funktiota $f$, jolla $$f(x) = 2x + 1.$$
- Täydennä alla oleva taulukko:
Muuttujan arvo Funktion arvo $x$ $f(x) = 2x + 1$ $1$ $f(1) = $ $7$ $0$ $-6$ $a$ $b$ - Mikä seuraavista on funktion $f$ kuvaaja? Käytä päättelyssä apuna taulukkoa, jonka täydensit a-kohdassa.
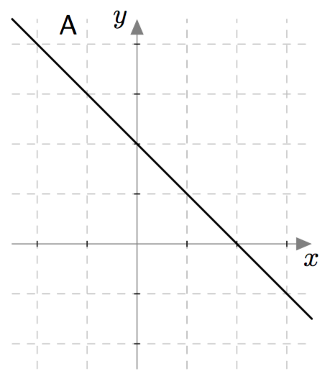
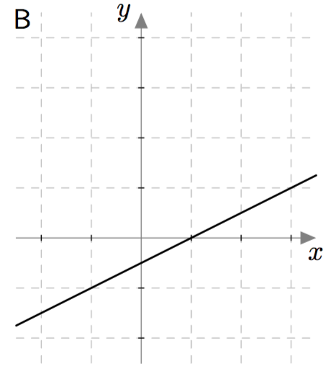
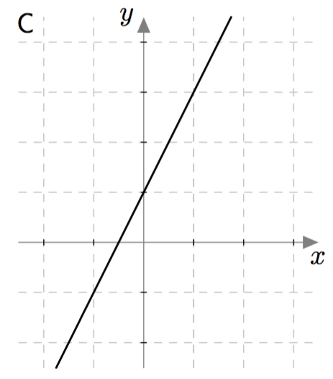
- Päättele kuvaajan avulla, millä muuttujan $x$ arvolla funktio $f$ saa arvon $0$. Toisin sanottuna etsi sellaiset luvut $x$, joilla $f(x) = 0$.
VASTAUS
- Kuvaaja on vaihtoehto C.
- $f(x) = 0$, jos ja vain jos $x = -0{,}5$.
Edellä tarkasteltu funktio $f$ on määritelty kaikilla reaaliluvuilla. Se tarkoittaa, että funktion $f$ arvo voidaan laskea, olipa muuttujan $x$ arvo mikä tahansa reaaliluku. Esimerkiksi jos $x = 135{,}8642$, on funktion $f$ arvo \begin{align*} f(135{,}8642) &= 2\cdot 135{,}8642 + 1 \\ &= 272{,}7284. \end{align*} On olemassa myös sellaisia funktiota, joiden arvo ei joidenkin muuttujan arvojen tapauksessa ole määritelty. Esimerkiksi funktion $$g(x) = \frac{1}{x-2}$$ arvo ei ole määritelty, jos $x = 2$, sillä nimittäjä on tällöin nolla. Tässä tilanteessa sanotaan, että funktio $g$ ei ole määritelty kohdassa $x = 2$. Funktion yhteyteen on hyvä liittää tieto siitä, millä muuttujan arvoilla funktio on määritelty: $$g(x) = \frac{1}{x-2}, \quad \text{ missä } x \neq 2.$$
Funktion määrittelyehto
Millä reaaliluvuilla seuraavat funktiot ovat määriteltyjä? Kirjoita jokaiselle funktiolle määrittelyehto.
- $f(x) = \dfrac{4}{x}$
- $g(x) = \dfrac{-12}{x+9}$
- $h(x) = \dfrac{6x+5}{2x-8}$
VASTAUS
- $x \neq 0$
- $x \neq -9$
- $x \neq 4$
Funktion kuvaaja
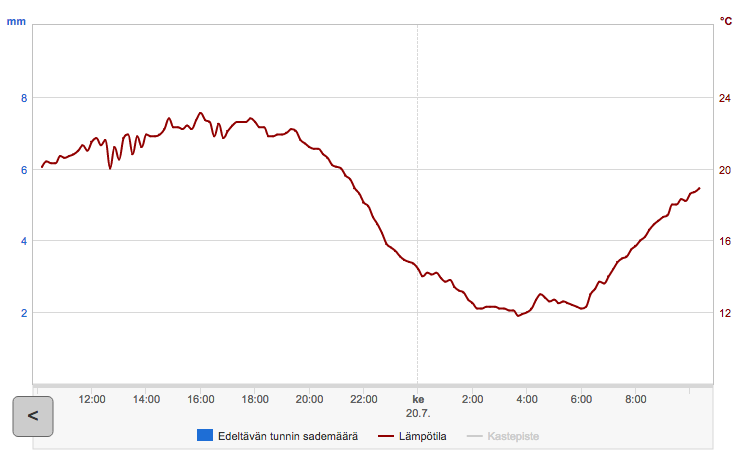
Funktion kuvaajan avulla voidaan tehdä päätelmiä sellaisissakin tilanteissa, joissa funktion esittäminen lausekkeen avulla on hankalaa. Esimerkiksi alla olevasta kuvassa on näkyvissä lämpötila ajan funktiona Ilmatieteen laitoksen Kumpulan havaintoasemalla Helsingissä (kuvankaappaus Ilmatieteenlaitoksen sivuilta).
Funktion kuvaajan tulkinta
Tarkastele yllä olevaa kuvaajaa, joka esittää lämpötilaa ajan funktiona.
- Mikä on ollut vuorokauden korkein lämpötila? Milloin se on saavutettu?
- Mikä on ollut vuorokauden matalin lämpötila? Milloin se on saavutettu?
- Millä aikavälillä lämpötila on ollut yli 20 astetta?
- Millä aikavälillä lämpötila on ollut alle 16 astetta?
VASTAUS
- Korkein lämpötila on ollut noin 23 astetta ja se on saavutettu noin klo 16.
- Matalin lämpötila on ollut noin 12 astetta ja se on saavutettu noin klo 4.
- Noin klo 10-21.
- Noin klo 23-8.30.
Funktion kuvaajan pisteen $y$-koordinaatti ilmaisee aina funktion arvon kyseisessä kohdassa. Esimerkiksi alla olevassa kuvassa funktion $f$ kuvaaja kulkee pisteen $(1,3)$ kautta. Tästä voidaan päätellä, että funktion $f$ arvo kohdassa $x = 1$ on $f(1) = 3$.
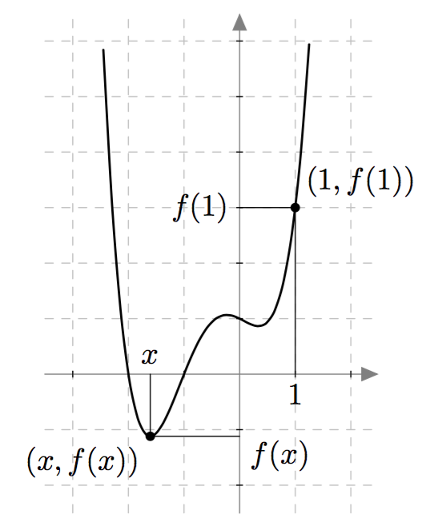
Funktion arvon lukeminen kuvaajasta
Alla on funktion $f$ kuvaaja. Päättele sen avulla vastaukset seuraaviin kysymyksiin:
- Minkä arvon funktio saa kohdassa $x = -1$?
- Mitä on $f(0)$?
- Mitä on $f(2)$? Saako funktio $f$ tämän arvon jossain muussakin kohdassa kuin kohdassa $x = 2$?

VASTAUS
- Kohdassa $x = -1$ funktio saa arvon $0$.
- $f(0) = -1$
- $f(2) = 3$ ja funktio saa saman arvon myös kohdassa $x = -2$.
Edellisen tehtävän funktion kuvaaja leikkaa $x$-akselin kohdassa $x = -1$ ja kohdassa $x = 1$. Näissä kohdissa kuvaajan pisteen $y$-koordinaatti on siis $0$. Nämä kohdat, joissa funktion arvo on $0$, on nimetty funktion nollakohdiksi:
MÄÄRITELMÄ: FUNKTION NOLLAKOHTA
Funktion $f$ nollakohta tarkoittaa sellaista muuttujan $x$ arvoa, jolla funktio saa arvon nolla eli $f(x) = 0$.
Funktion nollakohta
Alla on näkyvissä funktioiden $f$, $g$ ja $h$ kuvaajat. Millä näistä funktioista
- on tasan yksi nollakohta?
- on useita nollakohtia?
- ei ole yhtään nollakohtaa?
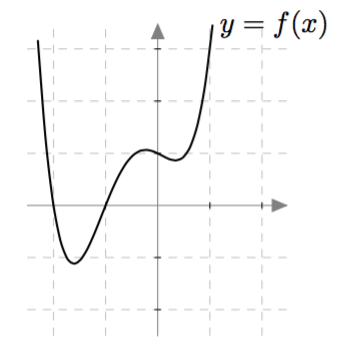
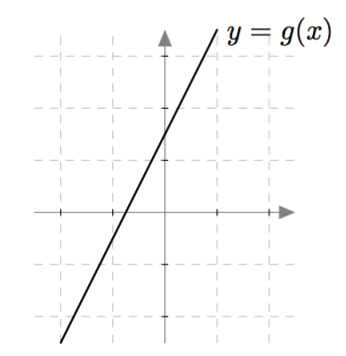
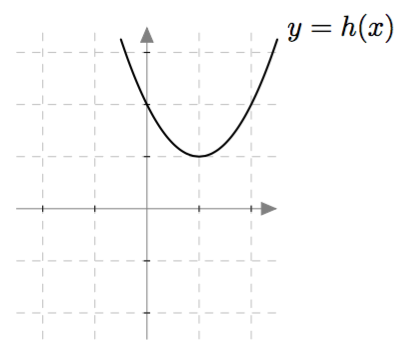
VASTAUS
- Funktiolla $g$ on tasan yksi nollakohta.
- Funktiolla $f$ on useita nollakohtia, tarkemmin sanottuna kaksi nollakohtaa.
- Funktiolla $h$ ei ole yhtään nollakohtaa.
Funktion kuvaajan tulkinta
Alla on funktion $g$ kuvaaja. Päättele sen avulla vastaukset seuraaviin kysymyksiin:
- Millä muuttujan $x$ arvolla funktio saa arvon $-2$?
- Onko funktiolla yksi tai useampia nollakohtia? Mitä ne ovat?
- Millä muuttujan $x$ arvolla $g(x) = 6$?
- Millä muuttujan $x$ arvoilla funktio $g$ saa arvon $g(4)$?
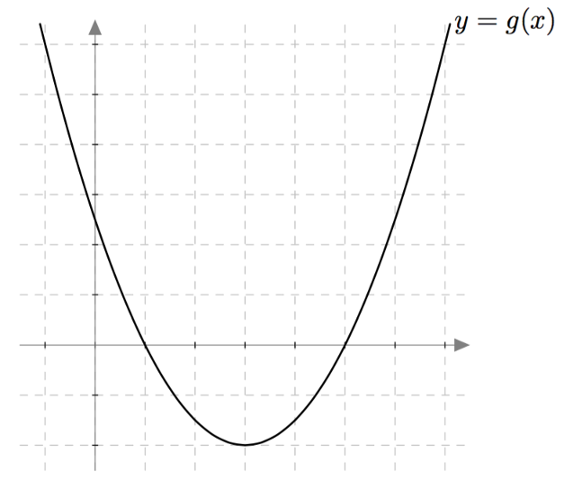
VASTAUS
- Arvolla $x = 3$.
- Kaksi nollakohtaa: $x_1 = 1$ ja $x_2 = 5$.
- $g(x) = 6$, jos ja vain jos $x = -1$ tai $x = 7$.
- Jos ja vain jos $x = 4$ tai $x = 2$.
Lukusuoran välejä ja niiden yhdistelmiä voidaan ilmaista merkkien $<$ (pienempi kuin), $>$ (suurempi kuin), $\leq$ (pienempi tai yhtä suuri kuin) ja $\geq$ (suurempi tai yhtä suuri kuin) avulla seuraavaan tapaan:
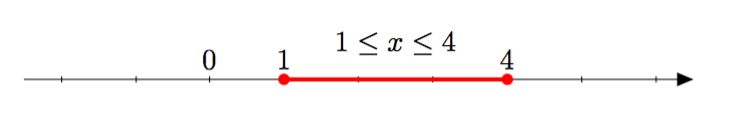


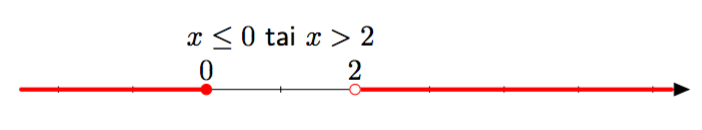
Lukusuoran välit
Havainnollista piirroksella lukusuoran välejä tai niiden yhdistelmiä
- $-2 < x \leq 1$
- $x < -3$
- $x < 2$ tai $x > 4$.
- Selitä omin sanoin, miksi ehdossa "$x \leq 0$ ja $x > 3$" ei ole järkeä.
Funktion kuvaajan tulkinta
Tarkastele alla olevaa funktion $f$ kuvaajaa. Millä muuttujan $x$ arvoilla
- funktio saa arvon nolla, eli $f(x)=0$
- funktion arvot ovat positiivisia eli $f(x)>0$
- funktion arvot negatiivisia eli $f(x)<0$?
Anna vastaus edellä harjoiteltuja lukusuoran välin merkintöjä käyttäen tai selitä omin sanoin.

VASTAUS
- Arvolla $x = 1{,}5 = \frac{3}{2}$.
- Jos ja vain jos $x$ on välillä $\left] \frac{3}{2}, \infty \right[$ eli $x > 1{,}5$.
- Jos ja vain jos $x$ on välillä $\left] -\infty, \frac{3}{2} \right[$ eli $x < 1{,}5$.
Funktion kuvaajan tulkinta
Tarkastele alla olevaa funktion $f$ kuvaajaa. Millaisia arvoja funktio saa eli mitä voit sanoa luvusta $f(x)$, jos
- $-1\leq x\leq 2$
- $x>0$
- $x\leq 1$?
Anna vastaus edellä harjoiteltuja lukusuoran välin merkintöjä käyttäen tai selitä omin sanoin.

VASTAUS
- Funktion arvot ovat välillä $[-5,1]$ eli $-5 \leq f(x) \leq 1$.
- Funktion arvot ovat välillä $\pa -3, \infty \pe$ eli $f(x) > -3$.
- Funktion arvot ovat välillä $\pa -\infty, -1]$ eli $f(x) \leq -1$.
Funktioiden arvoja voi vertailla piirtämällä niiden kuvaajat samaan koordinaatistoon kuten alla olevassa kuvassa. Siitä nähdään esimerkiksi, että funktiot $f$ ja $g$ saavat saman arvon kohdassa $a \approx 3{,}4$ ja tämä arvo on $f(a) = g(a) \approx 5$.
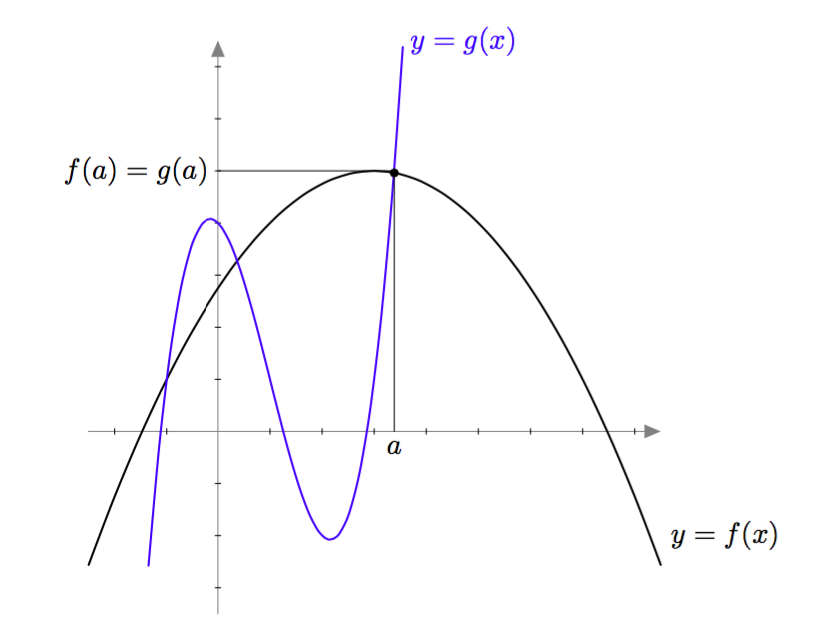
Funktioiden kuvaajien vertailu
Tarkastele edelleen yllä olevaa kuvaa, jossa näkyvät funktioiden $f$ ja $g$ kuvaajat.
- Saavatko funktiot $f$ ja $g$ saman arvon jossain muussakin kohdassa kuin kohdassa $x = a$? Missä?
- Kumpi funktioista saa suuremman arvon kohdassa $x = 0$?
- Kumpi funktioista saa suuremman arvon kohdassa $x = 1$?
- Selitä omin sanoin, miten kuvaajista näkyy se, että jollakin muuttujan $x$ arvolla funktion $g$ arvot ovat pienempiä kuin funktion $f$ arvot eli $g(x) < f(x)$.
VASTAUS
- Funktiot $f$ ja $g$ saavat saman arvon myös kohdissa $x \approx -1{,}1$ ja $x \approx 0{,}5$.
- Funktio $g$.
- Funktio $f$.
Seuraavien tehtävien avulla harjoitellaan funktion kuvaajan piirtämistä laskimella.
Funktion kuvaajan piirtäminen laskimella
Perehdy oman teknisen apuvälineesi käyttöön esimerkiksi opetus.tv:n opetusvideoiden avulla. Ne löytyvät osoitteesta opetus.tv -> työkalut -> valitse oma laskimesi -> funktiot ja kuvaajat. Harjoittele oman laitteesi käyttöä tekemällä seuraavaa:
- Piirrä funktion $f(x)=2x-1$ kuvaaja.
- Määritä kuvaajasta funktion $f$ nollakohta tai nollakohdat.
- Määritä laskimen laskinsovelluksen puolella funktion arvo, kun $x=4$.
- Piirrä samaan kuvaan funktion $g(x)=-x^2+4x+2$ kuvaaja.
- Määritä piirtämäsi kuvan avulla ne kohdat, joissa funktiot $f$ ja $g$ saavat saman arvon. Luettele kaikki tällaiset kohdat sekä niitä vastaavat funktioiden arvot.
- Määritä laskinsovelluksen avulla avulla ne kohdat, joissa funktiot $f$ ja $g$ saavat saman arvon, eli ratkaise yhtälö $f(x)=g(x)$. Saatko saman tuloksen kuin edellisessä kohdassa?
- Määritä funktioiden $f$ ja $g$ leikkauspisteiden $y$-koordinaatit määrittämällä jommankumman funktion arvo edellisessä kohdassa selvitetyillä muuttujan $x$ arvoilla.
VASTAUS
- Yksi nollakohta $x = \frac{1}{2}$.
- $f(4) = 7$
- Funktiot saavat saman arvon, jos ja vain jos $x = -1$ tai $x = 3$. Arvot: $f(-1) = -3$ ja $f(3) = 5$.
- Leikkauspisteet ovat $(-1,-3)$ ja $(3,5)$.
Funktion kuvaajan piirtäminen laskimella
- Piirrä funktion $f(x)=\sqrt{x}$ kuvaaja.
- Millaisia arvoja funktio $f$ saa?
- Millä muuttujan $x$ arvoilla funktio on määritelty, eli millaisilla luvuilla $x$ funktion kuvaaja on näkyvissä?
VASTAUS
- Funktion arvot ovat välillä $[0, \infty\pe$.
- Funktio on määritelty, jos $x \geq 0$.
Erilaisia funktioita
Funktioita voidaan luokitella eri tavoin. Voidaan esimerkiksi puhua polynomifunktioista, juurifunktioista, murtofunktioista, trigonometrisistä funktioista, eksponentti- ja logaritmifunktioista ja niin edelleen. Tiettyyn luokkaan kuuluvien funktioiden lausekkeet muistuttavat yleensä toisiaan ja niiden kuvaajissa on samoja piirteitä. Tässä kappaleessa tutkitaan kuvaajien avulla erityyppisten funktioiden ominaisuuksia.
Ensimmäiseksi tutkitaan niin sanottujen ensimmäisen asteen polynomifunktioiden ominaisuuksia.
MÄÄRITELMÄ: ENSIMMÄISEN ASTEEN POLYNOMIFUNKTIO
Funktiota $f$, joka on muotoa $f(x) = ax+b$, missä $a\neq 0$, sanotaan ensimmäisen asteen polynomifunktioksi.
Ensimmäisen asteen polynomifunktio
- Piirrä laskimellasi samaan kuvaan funktioiden $f(x)=0{,}5x + 1$, $g(x) = 2x+1$ ja $h(x) = -x+1$ kuvaajat.
- Mitä yhteistä näiden funktioiden kuvaajilla on? Entä mitä eroa niillä on?
- Kaikki tämän tehtävän funktiot ovat muotoa $x \mapsto ax +1$ eli ne kertovat muuttujaa $x$ jollakin luvulla $a$ ja lisäävät tulokseen luvun $1$. Miten luku $1$ näkyy funktioiden kuvaajissa?
- Pystytkö päättelemään kuvaajaa piirtämättä, millä korkeudella funktio $k(x) = x+4$ leikkaa $y$-akselin?
Ensimmäisen asteen polynomifunktio
- Piirrä laskimellasi samaan kuvaan funktioiden $f(x)=2x - 1$, $g(x) = 2x$ ja $h(x) = 2x+2$ kuvaajat.
- Mitä yhteistä näiden funktioiden kuvaajilla on? Entä mitä eroa niillä on?
- Kaikki tämän tehtävän funktiot ovat muotoa $x \mapsto 2x + b$ eli ne kertovat muuttujan $x$ kahdella ja lisäävät tulokseen luvun $b$. Miten kerroin $2$ näkyy funktioiden kuvaajissa?
Ensimmäisen asteen polynomifunktio
- Piirrä laskimellasi samaan kuvaan funktioiden $f(x)=-2x$ ja $g(x) = 2x$ kuvaajat.
- Mitä yhteistä näiden funktioiden kuvaajilla on? Entä mitä eroa niillä on?
- Miten voit päätellä kuvaajaa piirtämättä, onko funktion $h(x) = -3x+4$ kuvaaja nouseva vai laskeva suora?
Ensimmäisen asteen polynomifunktio
Selitä omin sanoin, miten voit päätellä ensimmäisen asteen polynomifunktion $f(x) = ax+b$ lausekkeesta,
- onko funktion kuvaaja nouseva vai laskeva suora
- miten jyrkästi kuvaaja nousee tai laskee
- missä kohdassa kuvaaja leikkaa $y$-akselin.
Voit tutkia edellisten tehtävien tuloksia tai piirtää vielä lisää ensimmäisen asteen polynomifunktioiden kuvaajia laskimellasi.
Piirtämällä paljon tietyntyyppisten funktioiden kuvaajia saa käsityksen siitä, miltä niiden kuvaajat yleensä näyttävät. Siitä on hyötyä, jos joutuu luonnostelemaan tai piirtämään tällaisen funktion kuvaajan kynän ja paperin avulla ilman laskinta tai tietokonetta.
Kuvaajan piirtäminen käsin
Tehtävänä on piirtää funktion $f(x) = -x+3$ kuvaaja ilman teknisiä apuvälineitä välillä $-3 \leq x \leq 6$.
- Määritä jokin kuvaajan piste esimerkiksi laskemalla funktion $f$ arvo jossakin kohdassa välillä $-3 \leq x \leq 6$ tai muuten päättelemällä (voit hyödyntää edellisten tehtävien havaintoja).
- Pystytkö piirtämään kuvaajan a-kohdan tiedon perusteella? Jos et, määritä jokin toinen kuvaajan piste samaan tapaan.
- Pystytkö piirtämään kuvaajan a- ja b-kohtien perusteella? Määritä tarvittaessa lisää kuvaajan pisteitä kunnes pystyt piirtämään kuvaajan koko välillä $-3 \leq x \leq 6$.
Seuraavassa tehtävässä piirretään erilaisten eksponenttifunktioiden kuvaajia. Eksponenttifunktioiden avulla voidaan mallintaa ja analysoida esimerkiksi sähkövirtapiirejä, aineen radioaktiivista hajoamista, kappaleen jäähtymistä, tietynlaisten kemiallisten reaktioiden nopeutta, populaatioiden koon kasvua, tautien leviämistä, pääoman karttumista korkonkorkolaskennassa, pyramidihuijauksia ja niin edelleen.
Eksponenttifunktio
- Piirrä laskimellasi samaan kuvaan funktioiden $f(x)=2^x$, $g(x) = 3^x$ ja $h(x) = 0{,}5^x$ kuvaajat.
- Mitä yhteistä näiden funktioiden kuvaajilla on? Entä mitä eroa niillä on? Tutki erityisesti kohtaa $x = 0$.
- Selitä omin sanoin, miten kantaluku $a$ vaikuttaa eksponenttifunktion $F(x) = a^x$ kuvaajan ulkonäköön.
Seuraavassa tehtävässä piirretään erilaisten logaritmifunktioiden kuvaajia. Logaritmifunktioiden avulla voidaan mallintaa äänenvoimakkuutta, maanjäristyksiä, liuoksen happamuutta tai emäksisyyttä ja niin edelleen.
Logaritmifunktio
- Piirrä laskimellasi samaan kuvaan funktioiden $f(x)=\log_2(x)$, $g(x) = \log_3(x)$ ja $h(x) = \log_{10}(x)$ kuvaajat.
- Mitä yhteistä näiden funktioiden kuvaajilla on? Entä mitä eroa niillä on? Tutki erityisesti kohtaa $x = 1$.
Logaritmifunktio ja eksponenttifunktio
- Piirrä laskimellasi samaan kuvaan funktioiden $f(x)=\log_2(x)$, $g(x) = 2^x$ ja $h(x) = x$ kuvaajat.
- Vertaa logaritmifunktion ja eksponenttifunktion kuvaajien sijaintia suhteessa kuvassa näkyvään suoraan. Mitä havaitset? Miten peili liittyy tähän tilanteeseen?
- Tee vastaava piirros kuin a-kohdassa mutta vaihda kantaluvuksi luku $3$. Havaitsetko saman ilmiön kuin b-kohdassa?
TEHTÄVÄSARJA II
Funktion määritelmä
Palauta mieleesi funktion käsitteen määritelmä ja päättele sen avulla, mitkä alla olevista kuvista voivat esittää jonkin funktion kuvaajaa välillä $-2 \leq x \leq 2$. Perustele jokaisen kuvan kohdalla omin sanoin, onko kysymyksessä funktion kuvaaja vai ei.
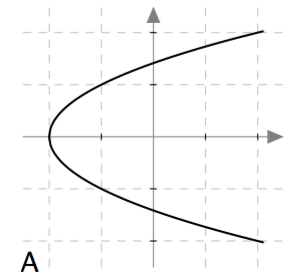
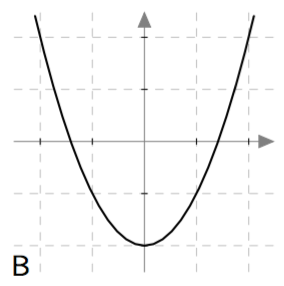
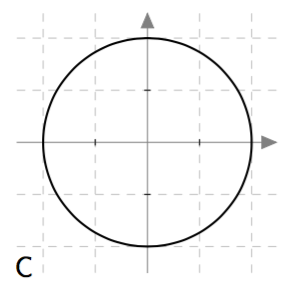
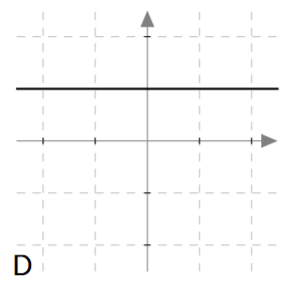
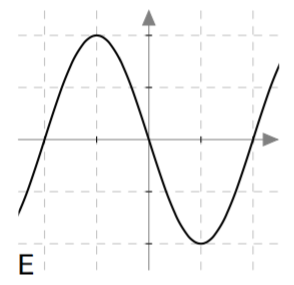
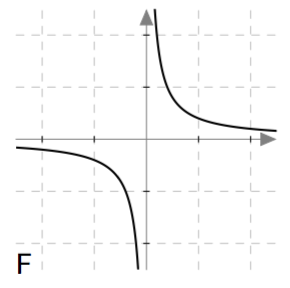
Vastaus
Funktion kuvaajaa välillä $-2 \leq x \leq 2$ voivat esittää vaihtoehdot B, D ja E. Vaihtoehdot A, C, ja F eivät esitä välillä $-2 \leq x \leq 2$ määriteltyä funktiota.
Funktion kuvaajan tulkinta
Alla on erään funktion $f$ kuvaaja. Päättele sen avulla vastaukset seuraaviin kysymyksiin:
- Mikä on funktion $f$ arvo kohdassa $x=5$?
- Mitä on $f(0)$?
- Onko funktiolla $f$ nollakohta tai nollakohtia? Jos on, mitä ne ovat?
- Millä muuttujan $x$ arvoilla funktion $f$ arvot ovat positiiviset?
- Millä muuttujan $x$ arvoilla funktion $f$ arvot ovat negatiiviset?
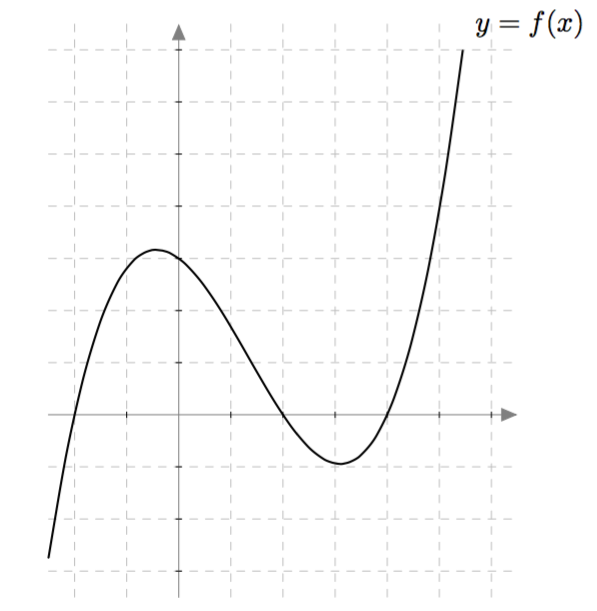
Vastaus
- $4$
- $f(0) = 3$
- Nollakohdat ovat $x = -2$, $x = 2$ ja $x = 4$.
- $-2 < x < 2$ tai $x > 4$
- $x < -2$ ja $2 < x < 4$
Funktion arvot ja funktion nollakohdat
Tutkitaan funktiota $f$, jolle $f(x) = \dfrac{x^2-3x-4}{x+2}$.
- Määritä laskemalla funktion arvot $\ f(2) \ $ ja $\ f(6)$.
- Päättele funktion $\ f$ lausekkeesta, mikä on sen määrittelyehto eli millä muuttujan arvoilla funktion arvon laskeminen on mahdollista.
- Piirrä funktion $\ f$ kuvaaja laskimella ja päättele seuraavien kohtien vastaukset kuvaajan avulla.
- Mikä on funktion $\ f$ arvo kohdassa nolla? Saako funktio tämän arvon jossain muussakin kohdassa?
- Onko funktiolla $\ f$ nollakohtia? Jos on, mitä ne ovat?
Vastaus
- $-\frac{3}{2}$
- $x \neq -2$
- $f(0) = -2$, myös kohdassa $x = 1$
- Kaksi nollakohtaa: $x = -1$ ja $x = 4$.
Funktion arvot ja funktion kuvaaja
Piirrä funktion $$g(x) = -\dfrac{1}{2}x^2+2x+2$$ kuvaaja laskimella välillä $-3 \leq x \leq 7$. Päättele kuvaajan avulla, missä kohdassa funktio $g$ saa arvon
- $2$
- $4$
- $6$.
- Mikä on funktion $g$ suurin arvo? Millä muuttujan $x$ arvolla funktio saa tämän arvon?
Vastaus
- $x = 0$ ja $x = 4$
- $x = 2$
- Ei millään
- Suurin arvo on $4$, kohdassa $x = 2$.
Funktion arvot ja funktion kuvaaja
Tutkitaan funktiota $f$, jolle $f(x) = -x^2-3x+4$.
- Laske funktion $f$ arvo kohdassa $x = -2$.
- Päättele edellisen kohdan tuloksen avulla, onko piste $(-2,5)$ funktion $f$ kuvaajalla, sen yläpuolella vai sen alapuolella.
- Piirrä funktion $f$ kuvaaja laskimella ja tarkista sen avulla, päädyitkö edellisessä kohdassa oikeaan johtopäätökseen.
Vastaus
- $f(-2) = 6$
- Kuvaajan alapuolella.
Funktion määrittelyjoukko ja funktion kuvaaja
Tutkitaan funktiota $h$, jolle $$h(x) = 2x + \dfrac{4}{1-x}.$$
- Päättele funktion $h$ lausekkeesta, mikä on sen määrittelyehto eli millä muuttujan arvoilla funktion arvon laskeminen on mahdollista.
- Piirrä funktion $h$ kuvaaja laskimella.
- Määritä kuvaajan avulla funktion $h$ nollakohdat.
- Määritä kuvaajan avulla funktion $h$ arvo kohdassa nolla. Saako funktio $h$ tämän arvon jossain toisessakin kohdassa? Missä?
Vastaus
- $x \neq 1$
- Kaksi nollakohtaa: $x = -1$ ja $x = 2$.
- $f(0) = 4$; funktio saa saman arvon myös kohdassa $x = 3$.
Funktion kuvaajan tulkinta
Oheisessa kuviossa on erään funktion $f(x)$ kuvaaja. Määritä kuvaajan avulla ne muuttujan $x$ arvot, joille $-2 \leq x \leq 4$ ja
- $f(x)=1$
- $f(x) \leq 0$.
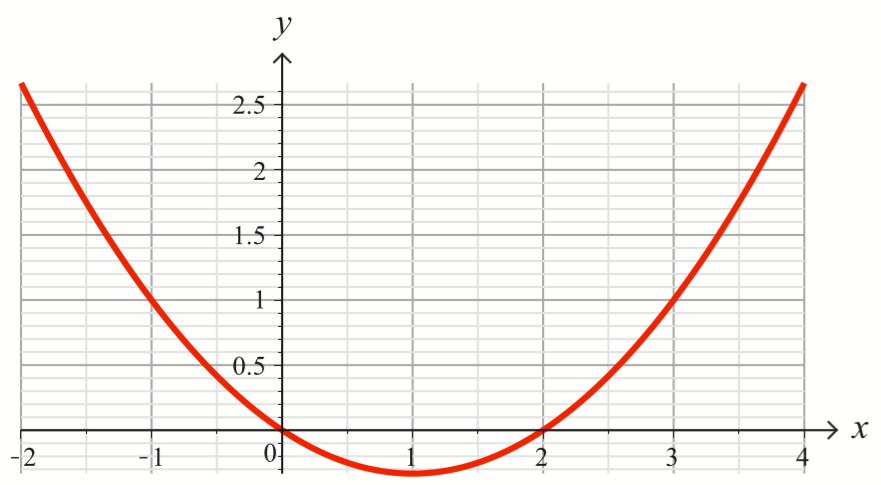
Vastaus
- Kaksi kohtaa: $x = -1$ ja $x = 3$
- $0 \leq x \leq 2$
Funktion kuvaajan tulkinta
Alla olevaan kuvaan on piirretty funktioiden $f(x) = 0{,}5x$ ja $g = -0{,}25x^2 + 2$ kuvaajat. Päättele niiden avulla vastaukset seuraaviin kysymyksiin:
- Missä kohdissa funktiot $f$ ja $g$ saavat saman arvon?
- Mitkä ovat yhtälön $0{,}5x = -0{,}25x^2+2$ ratkaisut?
- Millä muuttujan arvoilla funktio $g$ saa suurempia arvoja kuin funktio $f$?
- Mitkä luvut toteuttavat epäyhtälön $-0{,}25x^2+2 > 0{,}5x$?
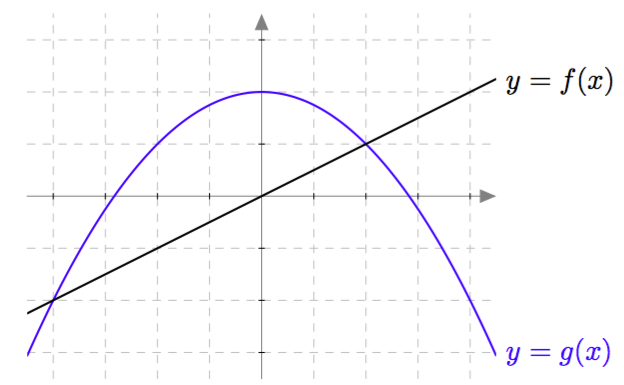
Vastaus
- Kaksi kohtaa: $x = -4$ ja $x = 2$
- $x = -4$ tai $x = 2$
- $-4 < x < 2$
- $-4 < x < 2$
Funktion kuvaajan tulkinta
Tutkitaan yhtälöä $0{,}25x-1{,}5 = 3-2^x$.
- Muodosta lausekkeet funktioille $f$ ja $g$ niin, että saat kirjoitettua tutkittavan yhtälön muodossa $f(x) = g(x)$.
- Piirrä funktioiden $f$ ja $g$ kuvaajat samaan koordinaatistoon laskimella.
- Päättele kuvaajan avulla, onko yhtälöllä $0{,}25x-1{,}5 = 3-2^x$ ratkaisua. Jos ratkaisuja on olemassa, mitä ne ovat?
Vastaus
- Esimerkiksi $f(x) = 0{,}25x - 1{,}5$ ja $g(x) = 3-2^x$
- $x = 2$
Funktio
Mittausten perusteella erään bussilinjan matka-ajan riippuvuutta ruuhkasta kuvaa funktio $f(x) = 0{,}0005x^2+0{,}01x+18$, missä $x$ on reitin vilkkaimpaan risteykseen saapuvien ajoneuvojen määrä yhden minuutin aikana. (Funktion arvo ilmaisee matka-ajan minuutteina.)
- Piirrä funktion $f$ kuvaaja välillä $0 \leq x \leq 200$ laskimellasi tai esimerkiksi Wolfram|Alphalla. Wolfram|Alphalla piirtäminen onnistuu komennolla plot $\ f(x) = 0{,}0005x^2+0{,}01x+18$, $\ x\ $ from 0 to 200.
- Päättele kuvaajasta, kuinka monta autoa risteykseen saa enintään saapua, jotta matka-aika olisi alle 30 minuuttia. Tarkenna kuvaa tarvittaessa pienentämällä tarkasteluväliä.
- Määritä laskemalla, miten paljon matka-aika pitenee, jos risteykseen minuutin aikana saapuvien autojen määrä kasvaa viidestäkymmenestä sataan.
Vastaus
- Noin 145 autoa.
- 4 min 15 s.
Funktio
Kun seurattiin paistolämpömittarin lukemia, havaittiin, että paistin sisälämpötila nousi koko ajan tasaisesti siten, että neljässä minuutissa lämpötila kohosi 2 ${}^\circ$C. Kun paisti laitettiin uuniin, lämpömittarin lukema oli 35 ${}^\circ$C.
- Muodosta lauseke funktiolle $f(t)$, joka kuvaa paistin sisälämpötilaa ajan $t$ funktiona.
- Piirrä funktion $f$ kuvaaja välillä $0 \leq t \leq 80$ laskimellasi tai esimerkiksi Wolfram|Alphalla.
- Keittokirjan mukaan paisti on kypsä, kun sen sisälämpötilan on 60 ${}^\circ$C. Päättele piirtämäsi kuvaajan avulla, kuinka kauan paistin kypsennys kestää. (Pienennä väliä $0 \leq t \leq 80$ tarvittaessa saadaksesi tarkemman tuloksen.)
- Jos paisti laitettiin uuniin klo 16, mihin aikaan se on valmis?
Vastaus
- $f(t) = 35 + 0{,}5t$
- 50 min
- 16:50
Ensimmäisen asteen polynomifunktio
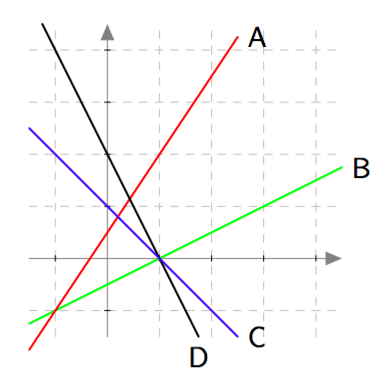
Yllä olevassa kuvassa on joidenkin ensimmäisen asteen polynomifunktioiden kuvaajia. Täydennä alla oleva taulukko liittämällä kuhunkin funktioon sen kuvaaja.
| Funktio | Kuvaaja |
|---|---|
| $\ f(x) = 0{,}5x-0{,}5 \ $ | |
| $g(x) = 1{,}5x+0{,}5$ | |
| $h(x) = -2x+2$ | |
| $k(x) = -x+1$ |
Vastaus
| Funktio | Kuvaaja |
|---|---|
| $\ f(x) = 0{,}5x-0{,}5 \ $ | B |
| $g(x) = 1{,}5x+0{,}5$ | A |
| $h(x) = -2x+2$ | D |
| $k(x) = -x+1$ | C |
Ensimmäisen asteen polynomifunktio
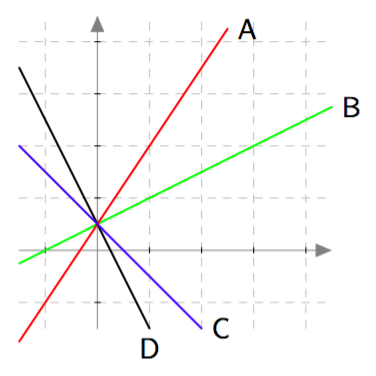
Yllä olevassa kuvassa on joidenkin ensimmäisen asteen polynomifunktioiden kuvaajia. Täydennä alla oleva taulukko liittämällä kuhunkin funktioon sen kuvaaja.
| Funktio | Kuvaaja |
|---|---|
| $\ f(x) = -x+0{,}5 \ $ | |
| $g(x) = -2x+0{,}5$ | |
| $\ h(x) = 0{,}5x+0{,}5 \ $ | |
| $k(x) = 1{,}5x+0{,}5$ |
Vastaus
| Funktio | Kuvaaja |
|---|---|
| $\ f(x) = 0{,}5x-0{,}5 \ $ | C |
| $g(x) = 1{,}5x+0{,}5$ | D |
| $h(x) = -2x+2$ | B |
| $k(x) = -x+1$ | A |
TEHTÄVÄSARJA III
Kahden sähköyhtiön A ja B hinnoittelu perustuu kiinteään kuukausittaiseen perusmaksuun, johon lisätään sähkön kulutuksen mukainen lisämaksu. Yhtiöiden tarjoamat hinnat selviävät alla olevasta taulukosta.
| Yhtiö | Perusmaksu €/kk | Yksikköhinta snt/kWh |
|---|---|---|
| A | 4,02 | 6,62 |
| B | 3,75 | 7,99 |
- Muodosta lausekkeet $a(x)$ ja $b(x)$ kummankin yhtiön tarjoaman sähkön kokonaishinnalle, kun sähköä kuluu $x$ kWh ja aikavälinä on yksi kuukausi.
- Kuinka suuri täytyisi sähkönkulutuksen olla kuukausittain, jotta kokonaishinnat olisivat samat?
- Kuinka suuri on sähkön kokonaishintojen välinen ero vuoden aikana, jos sähköä kuluu 2 000 kWh vuodessa?
Vastaus
- $a(x) = 0{,}0662x + 4{,}02$ ja $b(x) = 0{,}0799x + 3{,}75$
- 50 min
- 16:50
Ravintoliuoksessa kasvatettavan bakteeripopulaation yksilömäärä $N(t)$ kasvaa eksponentiaalisen mallin $N(t) = 1000 \cdot 1{,}25^t$ mukaisesti, kun aika $t$ ilmoitetaan tunteina.
- Mikä on populaation koko 24 tunnin kuluttua? Anna vastaus tuhannen bakteerin tarkkuudella.
- Kuinka monta prosenttia populaatio kasvaa jokaisen tunnin aikana?
- Kuinka monta tuntia kestää, että populaation koko ylittää miljoonan? Vihje: hyödynnä laskinta yhtälön ratkaisemisessa.
Vastaus
- Noin $212\,000$ yksilöä
- 25 %
- 31 tuntia
Erästä tuotetta myydään päivittäin 55 kappaletta, kun sen hinta on 35 euroa. Hinnan laskemisen on todettu vaikuttavan päivämyyntiin niin, että yhden euron alennus lisää aina menekkiä viidellä kappaleella.
- Mikä on päivittäisen myynnin kokonaisarvo, kun yhden tuotteen hinta on 35 euroa?
- Jos hintaa lasketaan $x$ euroa, kuinka monta kappaletta tuotetta myydään?
- Muodosta lauseke funktiolle $f(x)$, joka ilmaisee myynnin kokonaisarvon tilanteessa, jossa hintaa on laskettu $x$ euroa.
- Millä muuttujan $x$ arvoilla funktio $f$ on määritelty?
- Piirrä funktion $f$ kuvaaja välillä $5 \leq x \leq 20$ laskimellasi tai esimerkiksi Wolfram|Alphalla. Wolfram|Alphalla piirtäminen onnistuu esimerkiksi komennolla plot $f(x) = x+1$, $x$ from 5 to 20 (muuta funktion lauseke oikeaksi).
- Päättele kuvaajan avulla, kuinka paljon hintaa pitää alentaa, jotta päivittäisen myynnin kokonaisarvo on mahdollisimman suuri.
- Mikä tuotteen hinnaksi kannattaa valita, jos haluaa mahdollisimman suuren myynnin kokonaisarvon? Mikä tämä kokonaisarvo on?
Vastaus
- 1925 euroa
- $55 + 5x$
- $f(x) = (55 + 5x)(35-x)$
- $0 \leq x \leq 35$
- 12 euroa
- 23 euroa, 2645 euroa.
Joen rannalla oleva suorakulmion muotoinen alue aidataan kolmelta sivulta 100 m pitkällä köydellä.
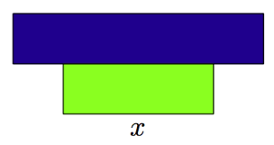
- Jos rannan suuntaisen sivun pituus on $x$, mikä on kahden muun sivun pituus?
- Muodosta lauseke funktiolle $A(x)$, joka ilmaisee aidatun alueen pinta-alan rannan suuntaisen sivun pituuden $x$ funktiona.
- Millä muuttujan $x$ arvoilla funktio $A(x)$ on määritelty?
- Piirrä funktion $A$ kuvaaja laskimellasi tai esimerkiksi Wolfram|Alphalla.
- Päättele kuvaajan avulla, kuinka pitkäksi rannan suuntainen sivu pitää valita, jotta aidatun alueen pinta-ala olisi mahdollisimman suuri.
- Mikä on aidatun alueen suurin mahdollinen pinta-ala?
Vastaus
- $\frac{100-x}{2}$
- $A(x) = \frac{100x-x^2}{2}$
- $0 < x < 100$
- 50 m
- 1250 m$^2$
Neliön muotoisen levyn sivun pituus on 300 mm. Levystä leikataa kuvion mukaisesti nurkat pois ja levy taitetaan laatikoksi, jossa ei ole kantta.
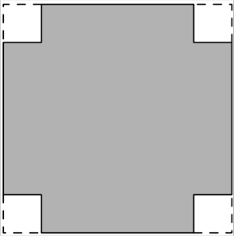
- Askartele paperista malli laatikolle.
- Esitä syntyneen laatikon tilavuus $V$ pois leikatun nurkkapalan sivun pituuden $h$ funktiona eli määritä $V(h)$.
- Millä muuttujan $h$ arvoilla funktio $V(h)$ on määritelty?
- Piirrä funktion $V(h)$ kuvaaja laskimella tai esimerkiksi Wolfram|Alphalla.
- Päättele kuvaajan avulla, kuinka suuri pituuden $h$ on oltava, jotta saadaan tilavuudeltaan mahdollisimman suuri laatikko.
- Laske funktion $V(h)$ avulla, mikä suurin mahdollinen tilavuus on. Anna vastaus kuutiodesimetreinä (dm$^3$) eli litroina (l). Selvitä tarvittaessa netistä, miten tilavuuden yksiköt mm$^3$, cm$^3$ ja dm$^3$ liittyvät toisiinsa.
Vastaus
- $V(h) = h\cdot (300-h)^2$
- $0 < h < 150$
- 100 mm
- 4 dm$^3$ eli 4 litraa.
Funktion määrittelyehto
Keksi esimerkki funktiosta, jonka määrittelyehto on
- $x \neq 1$
- $x \neq -9$
- $x \neq 2$ ja $x \neq 5$.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

