Rationaalifunktiot
Luvun tavoitteet
Tämän luvun tavoitteena on, että käsittelet sujuvasti rationaalilausekkeita ja sovellat tätä taitoa rationaaliyhtälöiden ja -epäyhtälöiden ratkaisemiseen sekä rationaalifunktioiden tutkimiseen. Osaat
- sieventää murto- ja rationaalilausekkeita
- ratkaista rationaaliyhtälön ja -epäyhtälön
- selvittää rationaalifunktion nollakohdat sekä kohdat, joissa rationaalifunktio ei ole määritelty
- laatia rationaalifunktion merkkikaavion
- tutkia, onko rationaalifunktiolla tietyssä kohdassa raja-arvo, ja määrittää raja-arvon, jos se on olemassa.
Murto- ja rationaalilausekkeet
Murtolauseke tarkoittaa kahden polynomin osamäärää. Esimerkiksi lausekkeet $$\frac{4x-1}{7-x^2} \quad \text{ ja } \quad \frac{9}{y^3+5y}$$ ovat murtolausekkeita. Murtolausekkeita voidaan käsitellä samoilla säännöillä kuin murtolukuja. Tässä kappaleessa palautetaan mieleen murtolukujen laskusäännöt ja harjoitellaan soveltamaan niitä murtolausekkeisiin.
Murtolukuja ja -lausekkeita voidaan sieventää supistamalla. Supistaminen onnistuu, jos sekä osoittaja että nimittäjä voidaan muuttaa tulomuotoon ja niistä löytyy yhteinen tekijä: $$ \frac{30}{21} = \frac{3\cdot 10}{3\cdot 7} = \frac{10}{7} $$ Murtolausekkeiden tapauksessa tulomuotoon muuttaminen saattaa vaatia yhteisen tekijän erottamisen sekä osoittajassa että nimittäjässä: $$ \frac{8x+4}{6x^2+3x} = \frac{4(2x+1)}{3x(2x + 1)} = \frac{4}{3x} $$ Tässä osoittajan termeillä oli yhteinen tekijä $4$, ja nimittäjän termeillä oli yhteinen tekijä $3x$. Kun osoittaja ja nimittäjä kirjoitettiin tulomuotoon, nähtiin molemmissa tekijänä myös lauseke $2x+1$. Se voitiin supistaa pois.
Murtolausekkeiden supistaminen
Tehtävänä on supistaa murtolauseke $$\dfrac{18x + 30}{12x}$$
- Kirjoita osoittaja tulomuodossa erottamalla mahdollisimman suuri yhteinen tekijä.
- Nimittäjä on jo valmiiksi tulo. Onko osoittajassa ja nimittäjässä jokin yhteinen tekijä? Supista se pois. Tarkista, jäikö osoittajaan ja nimittäjään vielä jokin yhteinen tekijä ja supista tarvittaessa uudestaan.
- Miltä tehtävän murtolauseke näyttää, kun se on supistettu mahdollisimman yksinkertaiseen muotoon?
VASTAUS
- $6(3x+5)$
- Osoittajassa ja nimittäjässä on molemmissa tekijänä luku 6.
- $\dfrac{3x+5}{2x}$
Murtolausekkeiden supistaminen
Tehtävänä on supistaa murtolauseke $$\dfrac{4x-7x^2}{9x}$$
- Kirjoita osoittaja tulomuodossa erottamalla yhteinen tekijä.
- Nimittäjä on jo valmiiksi tulo. Onko osoittajassa ja nimittäjässä jokin yhteinen tekijä? Supista se pois. Tarkista, jäikö osoittajaan ja nimittäjään vielä jokin yhteinen tekijä ja supista tarvittaessa uudestaan.
- Miltä tehtävän murtolauseke näyttää, kun se on supistettu mahdollisimman yksinkertaiseen muotoon?
VASTAUS
- $x(4-7x)$
- Osoittajassa ja nimittäjässä on molemmissa tekijänä $x$.
- $\dfrac{4-7x}{9}$
Murtolausekkeiden supistaminen
Tehtävänä on supistaa murtolauseke $$\dfrac{4x+2}{14x + 7}$$
- Kirjoita osoittaja tulomuodossa erottamalla mahdollisimman suuri yhteinen tekijä.
- Kirjoita nimittäjä tulomuodossa erottamalla mahdollisimman suuri yhteinen tekijä.
- Onko osoittajassa ja nimittäjässä jokin yhteinen tekijä? Supista se pois. Tarkista, jäikö osoittajaan ja nimittäjään vielä jokin yhteinen tekijä ja supista tarvittaessa uudestaan.
- Miltä tehtävän murtolauseke näyttää, kun se on supistettu mahdollisimman yksinkertaiseen muotoon?
VASTAUS
- $2(2x+1)$
- $7(2x+1)$
- Osoittajassa ja nimittäjässä on molemmissa tekijänä $2x+1$.
- $\dfrac{2}{7}$
Murtolukujen tapauksessa luvun ja sen vastaluvun osamäärä on helppo tunnistaa. Esimerkiksi $$\frac{\phantom{-}3}{-3} = -1.$$ Murtolausekkeiden tapauksessa vastaava tilanne voi näyttää esimerkiksi tältä: $$ \frac{x-8}{8-x} $$ Osoittajaa sieventämällä nähdään, että se on nimittäjän vastalauseke: \begin{align*} x-8 &= -8 + x \\ &=-1 \cdot (8-x). \end{align*} Osoittaja ja nimittäjä voidaan muuttaa tulomuotoon ja sen jälkeen supistaa yhteinen tekijä pois: $$ \frac{x-8}{8-x} = \frac{-1 \cdot (8-x)}{\phantom{-}1 \cdot (8-x)} = \frac{-1}{\phantom{-}1} = -1 $$
Murtolausekkeiden supistaminen
Kirjoita tässäkin tehtävässä kaikki välivaiheet huolellisesti näkyviin. Muista muuttaa osoittaja ja nimittäjä tulomuotoon ennen supistamista.
- Supista murtolauseke $$\dfrac{6-x}{x-6}$$
- Supista murtolauseke $$\dfrac{\phantom{-}5x+4}{-5x-4}$$
VASTAUS
- $-1$
- $-1$
MAA2-kurssilla johdetut summan ja erotuksen tulon sekä binomien neliöiden muistikaavat ovat välillä tarpeen murtolausekkeiden supistamisessa.
Murtolausekkeiden supistaminen
Tehtävänä on supistaa murtolauseke $$\dfrac{x^2-25}{9x + 45}$$
- Kirjoita osoittaja tulomuodossa sopivan muistikaavan avulla. Kertaa tarvittaessa muistikaavat MAA2-kurssin luvun 3 teoreemasta 3.
- Kirjoita nimittäjä tulomuodossa erottamalla mahdollisimman suuri yhteinen tekijä.
- Onko osoittajassa ja nimittäjässä jokin yhteinen tekijä? Supista se pois. Tarkista, jäikö osoittajaan ja nimittäjään vielä jokin yhteinen tekijä ja supista tarvittaessa uudestaan.
- Miltä tehtävän murtolauseke näyttää, kun se on supistettu mahdollisimman yksinkertaiseen muotoon?
VASTAUS
- $(x+5)(x-5)$
- $9(x+5)$
- Osoittajassa ja nimittäjässä on molemmissa tekijänä $x+5$.
- $\dfrac{x-5}{9}$
Ennen yhteen- ja vähennyslaskuja murtoluvut täytyy laventaa samannimisiksi. Laventaminen tarkoittaa, että osoittaja ja nimittäjä kerrotaan samalla luvulla. Tällöin murtoluvusta tulee eri näköinen mutta sen suuruus ei muutu. Esimerkiksi $$ \frac{1}{2} = \frac{6\cdot 1}{6 \cdot 2} = \frac{6}{12}. $$ Kun kaksi murtolukua lavennetaan samannimisiksi, yksi varma keino on laventaa ne toistensa nimittäjillä seuraavaan tapaan: \begin{align*} \frac{4}{\textcolor{blue}{5}} - \frac{3}{\textcolor{red}{7}} &= \frac{\textcolor{red}{7}\cdot 4}{\textcolor{red}{7}\cdot \textcolor{blue}{5}} - \frac{\textcolor{blue}{5}\cdot 3}{\textcolor{blue}{5}\cdot \textcolor{red}{7}} \\[2mm] &= \frac{28}{35} - \frac{15}{35} \\[2mm] &= \frac{28-15}{35} \\[2mm] &= \frac{13}{35} \end{align*} Lavennuksen jälkeen osoittajat voitiin yhdistää. Lopuksi vielä tarkistetaan, voiko tulosta supistaa. Tällä kertaa supistaminen ei onnistu, koska osoittajalla ja nimittäjällä ei ole yhteisiä tekijöitä.
Murtolausekkeiden yhteenlasku
Tehtävänä on sieventää summa $$\dfrac{x+2}{x} + \dfrac{5x}{x+1}$$
- Lavenna yhteenlaskettavat samannimisiksi.
- Muodosta ja sievennä osoittajien summa. Jätä lausekkeiden yhteinen nimittäjä tulomuotoon.
- Miltä vastaus näyttää, kun se on sievennetty mahdollisimman pitkälle?
VASTAUS
- $\dfrac{(x+1)(x+2)}{(x+1)x} + \dfrac{x\cdot 5x}{x(x+1)}$
- $\dfrac{6x^2 + 3x + 2}{x(x+1)}$
Murtolausekkeiden vähennyslaskussa on tärkeää huomata, että lausekkeiden välissä oleva miinusmerkki vaikuttaa sen perässä olevan murtolausekkeen koko osoittajaan. Esimerkiksi \begin{align*} \frac{1+x}{x^2} \textcolor{red}{-} \frac{\textcolor{blue}{4-x}}{x^2} &= \frac{1+x \textcolor{red}{-} \textcolor{blue}{(4-x)}}{x^2} \\[2mm] &= \frac{1+x \textcolor{red}{-} \textcolor{blue}{4}\textcolor{red}{+} \textcolor{blue}{x}}{x^2} \\[2mm] &= \frac{2x-3}{x^2} \end{align*}
Murtolausekkeiden vähennyslasku
Tehtävänä on sieventää erotus $$\dfrac{x-1}{x+2} - \dfrac{3x-7}{4x + 8}$$
- Lavenna murtolausekkeet samannimisiksi. Pystytkö tekemään tämän laventamalla vain ensimmäistä murtolauseketta?
- Muodosta ja sievennä osoittajien erotus.
- Miltä vastaus näyttää, kun se on sievennetty mahdollisimman pitkälle?
VASTAUS
- $\dfrac{4(x-1)}{4(x+2)} - \dfrac{3x-7}{4x +8}$
- $\dfrac{x+3}{4x+8}$
Murtolukujen kerto- ja jakolaskussa laventamista ei tarvitse tehdä. Kertolaskussa osoittajat kerrotaan keskenään ja nimittäjät kerrotaan keskenään. Esimerkiksi $$ \frac{1}{2} \cdot \frac{3}{5} = \frac{1\cdot 3}{2\cdot 5} = \frac{3}{10} $$ Usein kannattaa jo välivaiheessa tarkistaa, onko supistaminen mahdollista. Esimerkiksi $$ \frac{1}{2} \cdot \frac{4}{5} = \frac{1\cdot 4}{2\cdot 5} = \frac{2\cdot 2}{2\cdot 5} = \frac{2}{5} $$ Murtolausekkeiden kertolasku voidaan tehdä samaan tapaan kertomalla osoittajat keskenään ja nimittäjät keskenään. Ennen sulkujen avaamista kannattaa tarkistaa, onko osoittajassa ja nimittäjässä yhteisiä tekijöitä, jotka voisi supistaa pois. Esimerkiksi \begin{align*} \frac{x^2+x}{6x-9} \cdot \frac{3x}{x+1} &= \frac{(x^2+x) \cdot 3x}{(6x-9)(x+1)} \\[2mm] &= \frac{x\textcolor{blue}{(x+1)} \cdot \textcolor{red}{3}x}{\textcolor{red}{3}(2x-3)\textcolor{blue}{(x+1)}} \\[2mm] &= \frac{x\cdot x}{2x-3} \\[2mm] &= \frac{x^2}{2x-3} \end{align*}
Murtolausekkeiden kertolasku
Tehtävänä on sieventää tulo $$\dfrac{12x^2}{5x+15} \cdot \dfrac{10-25x}{4x}$$
- Kerro osoittajat ja nimittäjät keskenään mutta älä avaa vielä sulkuja.
- Mieti, onko osoittajassa ja nimittäjässä yhteisiä tekijöitä, jotka voisi supistaa pois. Tee kaikki mahdolliset supistukset.
- Miltä vastaus näyttää, kun se on sievennetty mahdollisimman pitkälle?
VASTAUS
- $\dfrac{12x^2(10-25x)}{(5x+15)4x}$
- Yhteisiä tekijöitä $5$ ja $4x$.
- $\dfrac{6x-15x^2}{x+3}$
Jakolasku saadaan suoritettua, kun kerrotaan jakajan käänteisluvulla. Esimerkiksi $10 : 2 = 5$ ja samaan tulokseen päästään myös kertomalla jakajan käänteisluvulla: $$ 10 \cdot \frac{1}{2} = \frac{10}{2} = 5. $$ Murtolausekkeiden tapauksessa kannattaa jälleen tehdä mahdolliset supistukset jo ennen sulkujen avaamista. Esimerkiksi \begin{align*} \frac{x^2+x}{x-1} : \textcolor{red}{\frac{x}{x^2-1}} &= \frac{x^2+x}{x-1} \cdot \textcolor{red}{\frac{x^2-1}{x}} \\[2mm] &= \frac{\textcolor{purple}{(x^2+x)}\textcolor{blue}{(x^2-1)}}{(x-1)x} \\[2mm] &= \frac{\textcolor{purple}{x(x+1)}\textcolor{blue}{(x-1)(x+1)}}{(x-1)x} \\[2mm] &= \frac{(x+1)(x+1)}{1} \\[2mm] &= (x+1)^2. \end{align*} Tässä käytettiin MAA2-kurssin luvun 3 teoreeman 3 summan ja erotuksen tulon kaavaa, jonka mukaan $$\textcolor{blue}{(x+1)(x-1) = x^2-1}.$$
Murtolausekkeiden jakolasku
Tehtävänä on sieventää osamäärä $$\dfrac{3x^2-3x}{2x+8} : \dfrac{6x-6}{x^2-16}$$
- Muuta jakolasku kertolaskuksi ja sievennä, mutta älä avaa vielä sulkuja.
- Mieti, onko osoittajassa ja nimittäjässä yhteisiä tekijöitä, jotka voisi supistaa pois. Tee kaikki mahdolliset supistukset.
- Miltä vastaus näyttää, kun se on sievennetty mahdollisimman pitkälle?
VASTAUS
- $\dfrac{(3x^2-3x)(x^2-16)}{(2x+8)(6x-6)}$
- Yhteisiä tekijöitä $3$, $x-1$ ja $x+4$. Huom. MAA2-kurssin luvun 3 teoreemasta 3 on apua.
- $\dfrac{x^2-4x}{4}$
Rationaalilauseke tarkoittaa polynomien ja murtolausekkeiden summaa. Myös pelkät polynomit ja pelkät murtolausekkeet luetaan mukaan rationaalilausekkeisiin. Rationaalilausekkeita ovat siis esimerkiksi \begin{align*} \frac{3x+13}{x^2} + 7x^3 - 2 \\[2mm] 6x^4-\frac{7}{9}x + 1 \\[2mm] \frac{1}{x} \end{align*} Kun rationaalilausekkeita sievennetään, voidaan käyttää murtolausekkeiden laskusääntöjä. Esimerkiksi \begin{align*} &\phantom{={}}\left(\frac{25}{x} - x\right) : (x+5) \\[2mm] &= \left(\frac{25}{x} - \frac{x^2}{x}\right) : (x+5) \\[2mm] &= \frac{25-x^2}{x} : (x+5) \\[2mm] &= \frac{25-x^2}{x} \cdot \frac{1}{x+5} \end{align*} Huomaa, että tässä jaettava sievennettiin ensin yhdeksi murtolausekkeeksi.
Rationaalilausekkeiden sieventäminen
Sievennä loppuun edellisen esimerkin lauseke $$ \frac{25-x^2}{x} \cdot \frac{1}{x+5} $$
VASTAUS
$\dfrac{5-x}{x}$
Vinkki: summan ja erotuksen tulo.
Rationaalilausekkeiden sieventäminen
Sievennä rationaalilauseke $$ \left(\frac{1}{2a+1} + \frac{1}{2a-1}\right) \cdot \left(1 - \frac{1}{4a^2}\right) $$
VASTAUS
$\dfrac{1}{a}$
Rationaalifunktiot ja -yhtälöt
Tässä kappaleessa tutustutaan niin sanottuihin rationaalifunktioihin. Ne ovat funktioita, jotka on määritelty jonkin rationaalilausekkeen avulla. Esimerkiksi $$ f(x) = 4-\frac{3}{5}x^2 + \frac{6x}{x^2-2} $$ on rationaalifunktio.
Rationaalifunktio
Alla on näkyvissä rationaalifunktioiden kuvaajia. Kopioi alla oleva taulukko vihkoosi ja täydennä se yhdistämällä oikea kuvaaja jokaiseen funktioon.
| Funktio | Kuvaaja |
|---|---|
| $\ f(x) = \dfrac{8x}{1+2x^2} \ $ | |
| $\ g(x) = \dfrac{1}{x-2} \ $ | |
| $\ h(x) = \dfrac{3}{1+x^2} \ $ | |
| $\ k(x) = \dfrac{1}{x} \ $ |
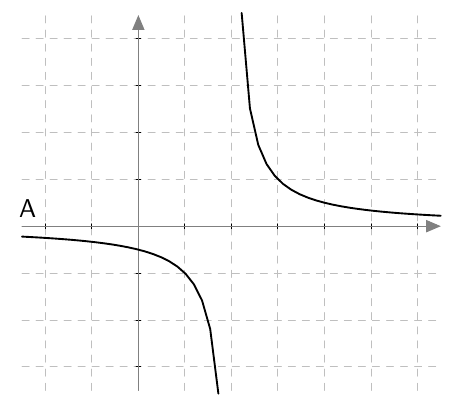
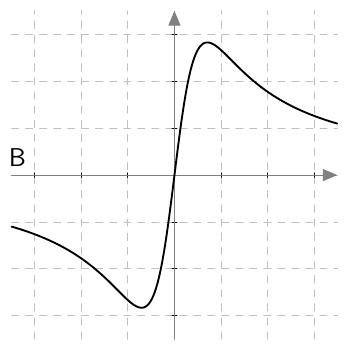
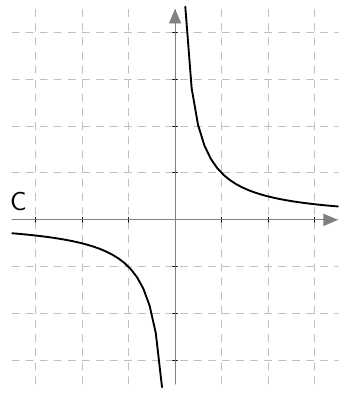
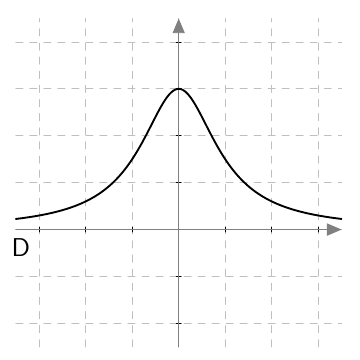
VASTAUS
Funktion $f$ kuvaaja on B.
Funktion $g$ kuvaaja on A.
Funktion $h$ kuvaaja on D.
Funktion $k$ kuvaaja on C.
Rationaalifunktio
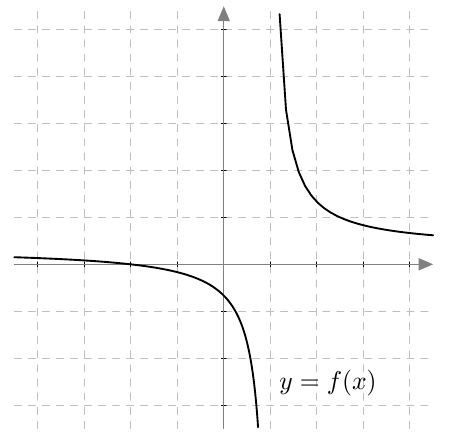
Alla on näkyvissä funktion $$f(x) = \frac{x+2}{3x-3}$$ kuvaaja.
- Missä kohdassa funktio $f$ ei ole määritelty? Miten tämä kohta näkyy funktion $f$ kuvaajassa?
- Miten voit funktion $f$ lausekkeen avulla selvittää, missä kohdassa funktio $f$ ei ole määritelty?
- Onko funktiolla $f$ nollakohtia? Miten ne näkyvät funktion $f$ kuvaajassa?
- Miten voit funktion $f$ lausekkeen avulla selvittää, onko funktiolla $f$ nollakohtia?
- Millä lukusuoran väleillä funktio $f$ saa positiivisia arvoja?
- Millä lukusuoran väleillä funktio $f$ saa negatiivisia arvoja?
- Missä kohdissa funktion arvojen merkki vaihtuu positiivisesta negatiiviseksi tai päinvastoin?
VASTAUS
- Funktio $f$ ei ole määritelty kohdassa $x = 1$.
- Funktio $f$ ei ole määritelty nimittäjän nollakohdissa, sillä nollalla jakamisen tulosta ei ole määritelty.
- Funktiolla $f$ on nollakohta $x = -2$.
- Ratkaisemalla osoittajan nollakohdat, tässä tapauksessa siis yhtälön $x + 2 = 0$.
- Väleillä $\pa -\infty, -2 \pe$ ja $\pa 1, \infty \pe$.
- Välillä $\pa -2,1\pe$.
- Funktion nollakohdassa ja kohdassa, jossa funktio ei ole määritelty.
Koska nollalla jakamista ei ole määritelty, rationaalifunktio ei ole määritelty kohdissa, joissa jokin siinä esiintyvistä nimittäjistä saa arvon nolla.
Rationaalifunktio
Tutkitaan funktiota $$f(x) = \frac{6x}{x-5} + \frac{3}{x+4}.$$
- Missä kohdissa funktio $f$ ei ole määritelty?
- Ratkaise funktion $f$ nollakohdat. Aloita esimerkiksi sieventämällä funktion lauseke yhdeksi murtolausekkeeksi.
- Tarkista vastauksesi piirtämällä funktion $f$ kuvaaja laskimella tai tietokoneella.
VASTAUS
- Funktio $f$ ei ole määritelty kohdissa $x = 5$ ja $x = -4$.
- Funktiolla $f$ on nollakohdat $x = -5$ ja $x = \frac{1}{2}$.
Kun tutkitaan, missä kohdassa jokin rationaalifunktio saa tietyn arvon, päädytään ratkaisemaan niin sanottu rationaaliyhtälö. Esimerkiksi rationaalifunktion $f$ nollakohdat voidaan löytää ratkaisemalla yhtälö $f(x) = 0$.
Rationaaliyhtälöiden ratkaisussa ensimmäinen tavoite on päästä eroon nimittäjistä. Tämä voidaan tehdä ainakin kahdella tavalla:
- Kerrotaan yhtälön kumpikin puoli kaikkien yhtälössä esiintyvien nimittäjien tulolla, jolloin nimittäjät voidaan supistaa pois.
- Muokataan yhtälön kumpikin puoli samannimisiksi murtolausekkeiksi sopivasti laventamalla. Tällöin voidaan päätellä, että yhtälö toteutuu, jos ja vain jos osoittajat ovat yhtä suuria.
Esimerkiksi yhtälön $$\frac{x}{2-x} + 1 = \frac{3}{x}$$ nimittäjistä voidaan hankkiutua eroon kummalla tahansa tavalla. Ennen ratkaisua kannattaa kuitenkin huomata, että yhtälö ei ole määritelty nimittäjien nollakohdissa eli jos $x = 2$ tai $x = 0$. Nämä luvut eivät siis missään tapauksessa kelpaa yhtälön ratkaisuksi.
- tapa: Yhtälössä esiintyvät nimittäjät $2-x$ ja $x$, joten kerrotaan yhtälön molemmat puolet tulolla $x(2-x)$ ja tehdään mahdolliset supistukset sen jälkeen: \begin{align*} \frac{x}{2-x} + 1 &= \frac{3}{x} \\[2mm] \frac{x\cdot \textcolor{blue}{x}\textcolor{red}{(2-x)}}{2-x} + \textcolor{blue}{x}\textcolor{red}{(2-x)} &= \frac{3\textcolor{blue}{x}\textcolor{red}{(2-x)}}{x} \\[2mm] x^2 + x(2-x) &= 3(2-x) \end{align*}
- tapa: Muokataan yhtälön kumpikin puoli samannimisiksi murtolausekkeiksi sopivasti laventamalla. \begin{align*} \frac{x}{2-x} + 1 &= \frac{3}{x} \\[2mm] \frac{x\cdot \textcolor{blue}{x}}{\textcolor{blue}{x}(2-x)} + \frac{\textcolor{blue}{x}\textcolor{red}{(2-x)}}{\textcolor{blue}{x}\textcolor{red}{(2-x)}} &= \frac{3\textcolor{red}{(2-x)}}{x\textcolor{red}{(2-x)}} \\[2mm] \frac{x^2 + x(2-x)}{x(2-x)} &= \frac{3(2-x)}{x(2-x)} \end{align*} Tämä yhtälö toteutuu, jos ja vain jos osoittajat ovat yhtä suuria eli $$x^2 + x(2-x) = 3(2-x)$$
Kun nimittäjistä on päästy eroon tavalla tai toisella, voidaan yhtälön ratkaisemista jatkaa normaalisti: \begin{align*} x^2 + x(2-x) &= 3(2-x) \\ x^2 + 2x - x^2 &= 6-3x \\ 5x &= 6 \\ x &= \frac{6}{5} \end{align*} Lopuksi tarkistetaan, että kysymyksessä todella on alkuperäisen yhtälön ratkaisu. Tämä voidaan tehdä sijoittamalla ratkaisuehdokas alkuperäiseen yhtälöön tai tarkistamalla, ettei kysymyksessä ole minkään yhtälössä esiintyvän nimittäjän nollakohta. Tässä tarkastellun yhtälön nimittäjien nollakohdat ovat $x = 0$ ja $x = 2$, joten $x = \frac{6}{5}$ todella on yhtälön ratkaisu. (Sijoittamalla havaitaan, että jos $x = \frac{6}{5}$, niin yhtälön vasen ja oikea puoli saavat kumpikin arvon $\frac{5}{2}$.)
Rationaaliyhtälö
Vertaile kahta edellä esitettyä tapaa, joilla rationaaliyhtälö saadaan muokattua tavalliseksi polynomiyhtälöksi.
- Mitä eroa näissä tavoissa on?
- Mitä yhteistä näissä tavoissa on?
- Kumpi näistä tavoista tuntuu itsellesi luontevammalta? Miksi?
Rationaaliyhtälö
Tehtävänä on ratkaista rationaaliyhtälö $$\frac{x}{1-x} + 4 = \frac{2}{3-x}$$
- Millä muuttujan arvoilla yhtälö ei ole määritelty?
- Poista yhtälöstä nimittäjät. Käytä jompaa kumpaa edellä esitetyistä tavoista. Millaiseen polynomiyhtälöön päädyt?
- Ratkaise polynomiyhtälö. Ovatko sen ratkaisut alkuperäisen yhtälön ratkaisuja?
VASTAUS
- Arvoilla $x = 1$ ja $x = 3$.
- Yhtälöön $3x-x^2 + 4(1-x)(3-x) = 2-2x$.
- Alkuperäinen yhtälö toteutuu, jos ja vain jos $x = \frac{5}{3}$ tai $x = 2$.
Rationaaliepäyhtälöt
Edellisessä kappaleessa harjoiteltiin rationaaliyhtälöiden ratkaisemista. Esimerkiksi yhtälö $$ \frac{2}{x-1} = 4 $$ voidaan ratkaista kertomalla sen molemmat puolet nimittäjällä $x-1$, jolloin yhtälö saa muodon $$ 2 = 4(x-1). $$ Vastaava tekniikka ei kuitenkaan toimi rationaaliepäyhtälöiden ratkaisemisessa, sillä epäyhtälömerkin käyttäytyminen riippuu siitä, kerrotaanko epäyhtälöä positiivisella vai negatiisivisella luvulla. Esimerkiksi \begin{align*} 1 &< 2 \quad \mid \ \cdot 3 \\ 3 &< 6 \end{align*} mutta \begin{align*} 1 &< 2 \quad \mid \ \cdot (-7) \\ -7 &> -14. \end{align*} Jos epäyhtälö $$ \frac{2}{x-1} > 4 $$ yritetään ratkaista samalla tavalla kuin vastaava yhtälö eli kertomalla sen molemmat puolet nimittäjällä $x-1$, päädytään hankalaan tilanteeseen, koska lausekkeen $x-1$ merkki riippuu muuttujan $x$ arvosta ja vaikuttaa myös epäyhtälömerkin käyttäytymiseen. Tässä kappaleessa opitaan ratkaisemaan rationaaliepäyhtälöt tavalla, johon ei tällaisia ongelmia liity. Menetelmä perustuu rationaalifunktioiden arvojen merkin tutkimiseen.
Tarkastellaan aluksi rationaalifunktion $$ f(x) = \frac{x+2}{3x-3} $$ kuvaajaa:

Kuvaajasta nähdään, että funktion arvojen merkki vaihtuu nollakohdassa $x = -2$ ja kohdassa $x = 1$, jossa funktio ei ole määritelty. On mahdollista osoittaa, että kysymyksessä ei ole sattuma:
TEOREEMA
Jos rationaalifunktion $f$ arvot $f(a)$ ja $f(b)$ ovat erimerkkiset, niin funktiolla on välillä $\pa a, b \pe$ (ainakin yksi) nollakohta tai kohta, jossa funktio ei ole määritelty.
Perustelu pohjautuu Bolzanon lauseeseen sekä tietoon siitä, että rationaalifunktiot ovat jatkuvia määrittelyjoukossaan.
Teoreemasta 3 seuraa, että rationaalifunktion arvojen merkki voi vaihtua vain funktion nollakohdissa sekä kohdissa, joissa funktio ei ole määritelty. Nämä kohdat täytyy siis ottaa huomioon, kun tutkitaan rationaalifunktion merkkiä.
Tarkastellaan esimerkiksi funktiota $$ g(x) = \frac{6x-8}{12x + 15}. $$ Ratkaistaan aluksi funktion $g$ nollakohdat. Huomaa, että osamäärä on nolla täsmälleen siinä tapauksessa, että osoittaja on nolla: \begin{align*} g(x) &= 0 \\[2mm] \frac{6x - 8}{12x + 15} &= 0 \\[2mm] 6x - 8 &= 0 \\[2mm] 6x &= 8 \\[2mm] x &= \frac{8}{6} = \frac{4}{3} \end{align*} Ratkaistaan myös nimittäjän nollakohdat eli kohdat, joissa funktio $g$ ei ole määritelty: \begin{align*} 12x + 15 &= 0 \\[2mm] 12x &= -15 \\[2mm] x &= -\frac{15}{12} = -\frac{5}{4} \end{align*} Laaditaan funktion merkkikaavio, johon merkitään funktion nollakohdat ja kohdat, joissa funktio ei ole määritelty.
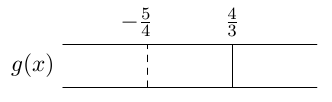
Valitaan jokaiselta merkkikaavion väliltä jokin kohta ja lasketaan funktion arvo tässä kohdassa. Esimerkiksi \begin{align*} g(-2) &= \frac{-12-8}{-24 + 15} = \frac{-20}{-9} = \frac{20}{9} \\[2mm] g(0) &= \frac{0-8}{0+15} = -\frac{8}{15} \\[2mm] g(2) &= \frac{12-8}{24 + 15} = \frac{4}{39} \end{align*} Täydennetään tiedot funktion arvojen merkistä merkkikaavioon:
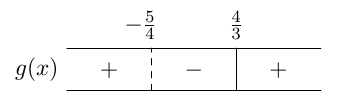 Funktio $g$ saa siis positiivisia arvoja lukusuoran väleillä $\pa -\infty, -\frac{5}{4} \pe$ ja $\pa \frac{4}{3}, \infty \pe$ ja negatiivisia arvoja lukusuoran välillä $\pa -\frac{5}{4}, \frac{4}{3} \pe$.
Funktio $g$ saa siis positiivisia arvoja lukusuoran väleillä $\pa -\infty, -\frac{5}{4} \pe$ ja $\pa \frac{4}{3}, \infty \pe$ ja negatiivisia arvoja lukusuoran välillä $\pa -\frac{5}{4}, \frac{4}{3} \pe$.
Rationaalifunktion merkki
Tehtävänä on selvittää, millä väleillä funktio $$ f(x) = \frac{6-2x}{2x+1} $$ saa positiivisia arvoja ja millä negatiivisia.
- Määritä funktion $f$ nollakohdat.
- Määritä ne kohdat, joissa funktio $f$ ei ole määritelty.
- Laadi funktion $f$ merkkikaavio. Millä väleillä funktio $f$ saa positiivisia arvoja ja millä negatiivisia?
- Tarkista vastauksesi piirtämällä funktion $f$ kuvaaja laskimella tai tietokoneella.
VASTAUS
- $x = 3$
- $x = -\frac{1}{2}$
Rationaaliepäyhtälön ratkaisemisessa ensimmäinen askel on palauttaa tilanne rationaalifunktion merkin tarkasteluun. Käytännössä epäyhtälöä muokataan niin, että sen toiselle puolelle jää nolla. Esimerkiksi epäyhtälö $$ \frac{x}{x+1} < \frac{1}{2-x} $$ muutetaan aluksi muotoon $$ \frac{x}{x+1} - \frac{1}{2-x} < 0. $$ Epäyhtälön ratkaisut löydetään, kun tutkitaan, millä väleillä vastaavan rationaalifunktion $$ f(x) = \frac{x}{x+1} - \frac{1}{2-x} $$ arvot ovat negatiivisia.
Kohdat, joissa funktio $f$ ei ole määritelty, ovat nimittäjien nollakohdat $x = -1$ ja $x = 2$. Ratkaistaan vielä funktion $f$ nollakohdat. Käytetään edellisessä kappaleessa harjoiteltua tapaa 1: \begin{align*} f(x) &= 0 \\[2mm] \frac{x}{x+1} - \frac{1}{2-x} &= 0 \\[2mm] \frac{x}{x+1} &= \frac{1}{2-x} \\[2mm] \frac{x\textcolor{blue}{(x+1)}\textcolor{red}{(2-x)}}{x+1} &= \frac{\textcolor{blue}{(x+1)}\textcolor{red}{(2-x)}}{2-x} \\[2mm] x(2-x) &= x+1 \\[2mm] 2x - x^2 &= x + 1 \\[2mm] -x^2 + x - 1 &= 0 \end{align*} Tämän toisen asteen yhtälön diskriminantti on negatiivinen: \begin{align*} D &= 1^2 - 4\cdot (-1)\cdot (-1) \\ &= 1-4 = -3. \end{align*} Yhtälöllä ei siten ole yhtään ratkaisua (MAA 2, teoreema 6). Tämä näkyy käytännössä myös siitä, että toisen asteen yhtälön ratkaisukaavassa juurrettava on negatiivinen.
Funktiolla $f$ ei siis ole nollakohtia, joten merkitään merkkikaavioon vain kohdat, joissa funktio ei ole määritelty.
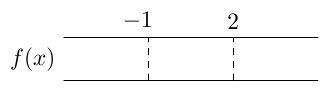
Valitaan jokaiselta merkkikaavion väliltä jokin kohta ja lasketaan funktion arvo tässä kohdassa. Esimerkiksi \begin{align*} f(-2) &= \frac{-2}{-1} - \frac{1}{4} = \frac{7}{4} \\[2mm] f(0) &= 0 - \frac{1}{2} = -\frac{1}{2} \\[2mm] f(3) &= \frac{3}{4} - \frac{1}{-1}= \frac{7}{4} \end{align*} Täydennetään tiedot funktion arvojen merkistä merkkikaavioon:
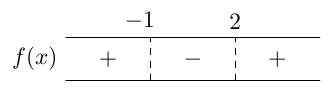
Alkuperäinen epäyhtälö toteutuu, jos ja vain jos funktion $f$ arvot ovat negatiivisia. Epäyhtälö $$ \frac{x}{x+1} < \frac{1}{2-x} $$ siis toteutuu, jos ja vain jos $-1 < x < 2$.
Rationaaliepäyhtälö
Tehtävänä on ratkaista epäyhtälö $$ \frac{x-5}{x+3} \geq 2. $$
- Muokkaa epäyhtälöä niin, että sen oikealle puolelle jää nolla.
- Millaisen rationaalifunktion merkkiä tutkimalla löydät alkuperäisen epäyhtälön ratkaisut? Laadi tämän funktion merkkikaavio.
- Millä muuttujan arvoilla alkuperäinen epäyhtälö toteutuu?
- Harjoittele teknisen apuvälineen käyttöä rationaalifunktioiden, -yhtälöiden ja -epäyhtälöiden tutkimisessa. Katso Texas Nspiren ohjevideo halutessasi täältä ja käytä oppimaasi tämän tehtävän ratkaisemiseen tai tarkistamiseen.
VASTAUS
- $\dfrac{x-5}{x+3} - 2 \geq 0$
- $f(x) = \dfrac{x-5}{x+3} - 2$
- $-11 \leq x < -3$ (huom. kohdassa $x = -3$ epäyhtälön vasen puoli ei ole määritelty).
Rationaalifunktion raja-arvo
Edellisessä luvussa tutustuttiin funktion raja-arvon käsitteeseen. Tässä kappaleessa tutkitaan tarkemmin rationaalifunktioiden raja-arvoja.
Rationaalifunktion raja-arvo
Alla on näkyvissä osa funktion $$f(x) = \frac{1}{x+1}$$ kuvaajasta.
- Missä kohdassa funktio $f$ ei ole määritelty?
- Onko funktiolla $f$ raja-arvo kohdassa
- $x = -2$
- $x = -1$
- $x = 0$?
- Jos b-kohdassa raja-arvo on olemassa, mikä se on? Käytä vastausten ilmoittamiseen merkintätapaa $$\lim_{x \rightarrow a} f(x) = b.$$
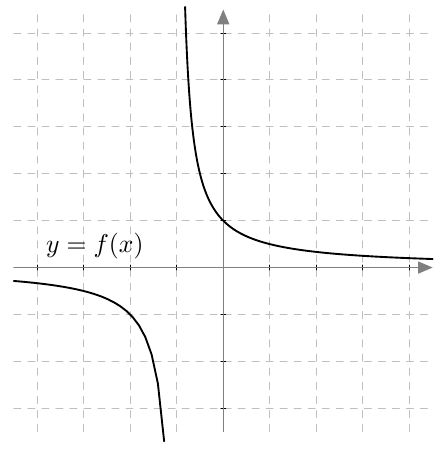
VASTAUS
- Funktio ei ole määritelty kohdassa $x = -1$.
- Funktiolla $f$ on raja-arvo kohdissa $x = -2$ ja $x = 0$. Funktiolla $f$ ei ole raja-arvoa kohdassa $x = -1$.
- Raja-arvot ovat seuraavat: \begin{align*} \lim_{x \rightarrow -2} f(x) &= -1 \\[1mm] \lim_{x \rightarrow 0} f(x) &= 1 \end{align*}
Rationaalifunktion raja-arvo
Alla on näkyvissä osa funktion $$g(x) = \frac{x^2-1}{2x-2}$$ kuvaajasta.
- Missä kohdassa funktio $g$ ei ole määritelty?
- Onko funktiolla $g$ raja-arvo kohdassa
- $x = -1$
- $x = 1$
- $x = 3$?
- Jos b-kohdassa raja-arvo on olemassa, mikä se on? Käytä vastausten ilmoittamiseen merkintätapaa $$\lim_{x \rightarrow a} f(x) = b.$$
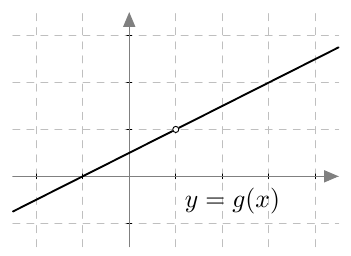
VASTAUS
- Funktio ei ole määritelty kohdassa $x = 1$.
- Funktiolla $f$ on raja-arvo kaikissa mainituissa kohdissa.
- Raja-arvot ovat seuraavat: \begin{align*} \lim_{x \rightarrow -1} f(x) &= 0 \\[1mm] \lim_{x \rightarrow 1} f(x) &= 1 \\[1mm] \lim_{x \rightarrow 3} f(x) &= 2 \end{align*}
Edellisistä tehtävistä havaitaan, että raja-arvon olemassaolon kannalta kriittisimpiä ovat ne kohdat, joissa rationaalifunktio ei ole määritelty. Jos funktiolla on tällaisessa kohdassa raja-arvo, voidaan se löytää supistamalla funktion lauseketta. Esimerkiksi edellisen tehtävän funktio $$g(x) = \frac{x^2-1}{2x-2}$$ ei ole määritelty nimittäjän nollakohdassa $x = 1$. Lauseketta voidaan kuitenkin supistaa niin, että raja-arvo voidaan määrittää: \begin{align*} \frac{x^2-1}{2x-2} &= \frac{(x+1)(x-1)}{2(x-1)} \\[2mm] &= \frac{x+1}{2} \xrightarrow[x \rightarrow 1]{} \frac{1+1}{2} = 1 \end{align*} Tässä osoittaja ja nimittäjä muokattiin ensin tulomuotoon. Supistamisen jälkeen tutkittiin, mitä lausekkeelle tapahtuu, kun lähestytään kohtaa $x = 1$.
Rationaalifunktion raja-arvo
Alla on näkyvissä osa funktion $$h(x) = \frac{3x}{x^2-4x}$$ kuvaajasta.
- Missä kohdissa funktio $h$ ei ole määritelty?
- Onko funktiolla $h$ raja-arvo kohdassa
- $x = 0$
- $x = 4$?
- Jos b-kohdassa raja-arvo on olemassa, mikä se on? Muokkaa funktion lauseketta niin, että supistaminen on mahdollista, ja määritä tarkka raja-arvo samaan tapaan kuin edellä tehtiin.
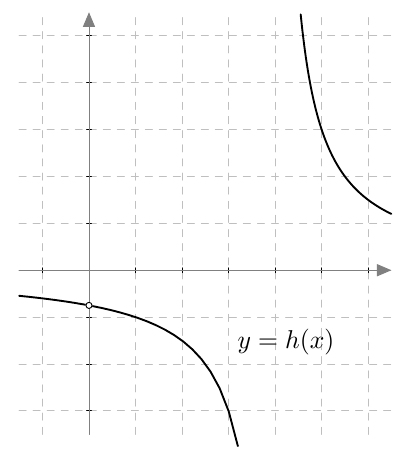
VASTAUS
- Funktio ei ole määritelty kohdissa $x = 0$ ja $x = 4$.
- Funktiolla $f$ on raja-arvo kohdassa $x = 0$. Funktiolla ei ole raja-arvoa kohdassa $x = 4$.
- \begin{align*} \frac{3x}{x^2-4x} &= \frac{3x}{x(x-4)} \\[2mm] &= \frac{3}{x-4} \xrightarrow[x \rightarrow 0]{} \frac{\phantom{-}3}{-4} = -\frac{3}{4}. \end{align*}
Jos rationaalifunktio on määritelty tarkastelukohdassa, saadaan raja-arvo selvitettyä ilman supistamista. Esimerkiksi $$\frac{3x}{x^2-4x} \xrightarrow[x \rightarrow 7]{} \frac{3\cdot 7}{7^2 - 4\cdot 7} = \frac{21}{21} = 1,$$ joten edellisen tehtävän funktiolle $$h(x) = \frac{3x}{x^2-4x}$$ pätee $$\lim_{x\rightarrow 7} h(x) = 1.$$ Tämä itse asiassa tarkoittaa, että funktion $h$ raja-arvo kohdassa $x = 7$ on sama kuin funktion arvo kohdassa $x = 7$: $$\lim_{x\rightarrow 7} h(x) = h(7).$$ Luvussa 2 esitetty jatkuvuuden määritelmän ehto siis toteutuu, joten funktio $h$ on jatkuva kohdassa $x = 7$.
On mahdollista osoittaa, että vastaava ilmiö koskee kaikkia rationaalifunktioita:
TEOREEMA
Rationaalifunktio on jatkuva koko määrittelyjoukossaan.
Teoreeman 4 mukaan rationaalifunktion raja-arvo on sama kuin funktion arvo kaikissa kohdissa, joissa funktio on määritelty. Erityistä tarkastelua vaativat vain nimittäjän nollakohdat, joissa funktio ei ole määritelty.
Rationaalifunktion raja-arvo
Tutki, onko funktiolla $$f(x) = \frac{x^3-3x^2}{x-3}$$ raja-arvo kohdassa
- $x = -5$
- $x = 3$
- $x = 11$.
VASTAUS
- ${\displaystyle\lim_{x\rightarrow -5} f(x) = 25}$.
- ${\displaystyle\lim_{x\rightarrow 3} f(x) = 9}$.
(Osoittajassa ja nimittäjässä on tekijänä $x-3$, joten sen voi supistaa pois.) - ${\displaystyle\lim_{x\rightarrow 11} f(x) = 121}$.
Tutkitaan seuraavaksi funktiota $$g(x) = \frac{x^2-16}{x^2 - 8x + 16}$$ kohdassa $x = 4$.
Havaitaan, että kohdassa $x = 4$ nimittäjä saa arvon nolla, joten funktio $g$ ei ole määritelty. Muistikaavojen \begin{align*} (a+b)(a-b) &= a^2 + b^2 \quad \text{ ja}\\ (a-b)^2 &= a^2 -2ab + b^2 \end{align*} avulla funktion lauseke saadaan muotoon, jossa supistaminen on mahdollista: \begin{align*} \frac{x^2-16}{x^2 - 8x + 16} &= \frac{(x+4)(x-4)}{(x-4)^2} \\[2mm] &= \frac{x+4}{x-4} \end{align*} Huomataan, että tulos ole määritelty kohdassa $x = 4$, vaikka kaikki mahdolliset supistukset on tehty. Tällaisessa tilanteessa funktiolla ei ole raja-arvoa, vaan funktion arvot kasvavat tai pienenevät rajatta tarkastelukohdan läheisyydessä.
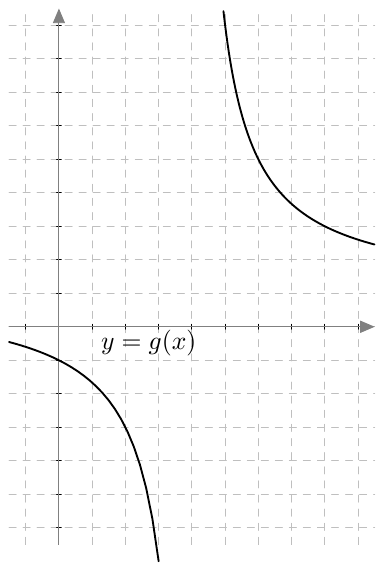
Rationaalifunktion raja-arvo
Tutki, onko funktiolla $$f(x) = \frac{x^2-4}{4x^2-8x}$$ raja-arvo kohdassa
- $x = -1$
- $x = 0$
- $x = 2$
- $x = 5$.
- Katso tästä ohjevideo, miten raja-arvoja voi laskea Texas Nspirellä, ja tarkista aiemmat kohdat teknisellä apuvälineellä.
VASTAUS
- ${\displaystyle\lim_{x\rightarrow -1} f(x) = -\frac{1}{4}}$.
- Raja-arvoa ei ole olemassa. Funktion lauseke supistuu muotoon $\frac{x+2}{4x}$, joka ei ole määritelty kohdassa $x = 0$. Pidemmälle sitä ei voi supistaa.
- ${\displaystyle\lim_{x\rightarrow 2} f(x) = \frac{1}{2}}$.
- ${\displaystyle\lim_{x\rightarrow 5} f(x) = \frac{7}{20}}$.
TEHTÄVÄSARJA II
Rationaaliyhtälö
Ratkaise yhtälö
- $\dfrac{x}{x+1} + \dfrac{x-1}{x} = 2$
- $\dfrac{x}{x-1} = 1 - \dfrac{1}{1-x}$
Vastaus
- $x = -\frac{1}{2}$
- $x \neq 1$
Rationaaliepäyhtälö
Kahdesta peräkkäisestä parittomasta kokonaisluvusta pienemmän ja suuremman osamäärä on pienempi kuin $\frac{3}{4}$. Mitkä luvut voivat olla kysymyksessä?
Vinkki: Jos pienempi luvuista on $x$, niin mikä suurempi luvuista on?
Vastaus
Mahdolliset peräkkäisten parittomien kokonaislukujen muodostamat lukuparit ovat $(-1,1)$, $(1,3)$, $(3,5)$ ja $(5,7)$. Näitä vastaavat osamäärät ovat $$ \dfrac{-1}{1} = -1, \ \dfrac{1}{3}, \ \dfrac{3}{5} \ \text{ ja } \ \dfrac{5}{7}. $$
Rationaaliyhtälö
Millä vakion $a$ arvoilla yhtälöllä $$ \frac{x}{x-1} = \frac{x+a}{x+1} $$ ei ole ratkaisua?
Vastaus
Jos $a = 1$ tai $a = 2$.
Rationaaliepäyhtälö
Millä muuttujan $x$ arvoilla $f(x) \leq 0$, jos
- $f(x) = \dfrac{x^2-6x}{x-3}$
- $f(x) = \dfrac{x^2-6x}{(x-3)^2}$?
Vastaus
- $x \leq 0$ tai $3 < x \leq 6$
- $0 \leq x \leq 6$ ja $x \neq 3$
Rationaalifunktion raja-arvo
Määritä raja-arvo tai perustele, että sitä ei ole olemassa:
- ${\displaystyle \lim_{x \rightarrow 0} \frac{x^2 + x}{x}}$
- ${\displaystyle \lim_{x \rightarrow 3} \frac{x^3 - 3x^2}{x-3}}$
Vastaus
- 1
- 9
Rationaalifunktion raja-arvo
Määritä raja-arvo tai perustele, että sitä ei ole olemassa:
- ${\displaystyle \lim_{x \rightarrow 1} \frac{1}{x-1}\left(\frac{2}{x+1} - \frac{1}{x}\right)}$
- ${\displaystyle \lim_{x \rightarrow 2} \left( x + 1 + \frac{1}{x} \right)}$
Vastaus
- $\frac{1}{2}$
- $\frac{7}{2}$
Rationaalifunktion raja-arvo
Määritä raja-arvo tai perustele, että sitä ei ole olemassa:
- ${\displaystyle \lim_{x \rightarrow 1} \frac{x^2 + 2x - 3}{x-1}}$
- ${\displaystyle \lim_{x \rightarrow -1} \frac{2x^2 + x - 1}{3x^2 + 5x + 2}}$
Vinkki: MAA2-kurssin teoreema 8.
Vastaus
- 4
- 3
TEHTÄVÄSARJA III
Määritä vakiolle $a$ sellainen arvo, että funktio $$ f(x) = \begin{cases} \dfrac{x^2-x-2}{x-2} &\text{ jos $x \neq 2$} \\[2mm] a &\text{ jos $x = 2$} \end{cases} $$ on jatkuva kaikkialla.
Vastaus
$a = 3$
Tutkitaan funktiota $$ f(x) = \frac{x^2-1}{x^2-x-2}. $$
- Missä kohdissa funktio $f$ ei ole määritelty?
- Voisiko funktion määritelmää täydentää niin, että funktiosta tulisi jatkuva myös niissä kohdissa, joissa se ei nyt ole määritelty?
Vastaus
- Kohdissa $-1$ ja $2$.
- Kohdassa $-1$ funktiolla on raja-arvo $\frac{2}{3}$, joten jos määritellään $$ f(-1) = \frac{2}{3}, $$ niin $f$ on jatkuva kohdassa $-1$. Kohdassa $2$ funktiolla ei ole raja-arvoa, joten funktion arvoa kohdassa $2$ ei ole mahdollista määritellä niin, että funktiosta tulisi jatkuva.
- Laske $$ \lim_{x \rightarrow 2} \frac{x^2 - 4}{x - 2}. $$
- Ratkaise epäyhtälö $$ \left| \frac{x^2-4}{x-2} - 4 \right| < 0{,}01. $$
[Pitkä S2011/6]
Vinkki: kertaa tarvittaessa b-kohtaa varten MAA5-kurssin luku 5.
Vastaus
- $$ \lim_{x \rightarrow 2} \frac{x^2 - 4}{x - 2} = \lim_{x \rightarrow 2} (x + 2) = 4. $$
- $1{,}99 < x < 2$ tai $2 < x < 2{,}01$. (Huomaa, että epäyhtälö ei ole määritelty, jos $x = 2$.)
Määritä vakio $a$ siten, että funktiolla $$ f(x) = \frac{3x^3 - x^2 - 12x + a}{x+2} $$ on raja-arvo kohdassa $x = -2$. Mikä tämä raja-arvo on?
[Pitkä S2008/12]
Vastaus
Funktion lauseke voidaan supistaa, jos osoittajalla ja nimittäjällä on yhteinen nollakohta (ks. MAA2-kurssin teoreema 9). Näin saadaan selville, että raja-arvo on olemassa, jos $a = 4$. Raja-arvo on $28$.
Ratkaise epäyhtälö $$ \frac{x^2 + 7x + 2}{x - 3} > 1. $$ [Pitkä K2007/6]
Vastaus
$-5 < x < -1$ tai $x > 3$.
Ratkaise
- epäyhtälö $\dfrac{2x+1}{x-1} \geq 3$
- yhtälö $\dfrac{1+x}{1-x} = \dfrac{1-x^2}{1 + x^2}$
[Pitkä S2011/3b & S2013/1b]
Vastaus
- $1 < x \leq 4$
- $x = 0$ tai $x = -1$
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

