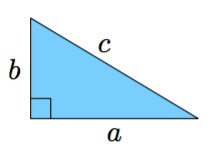
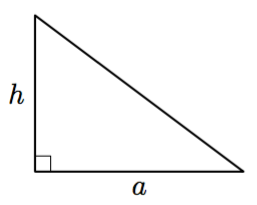
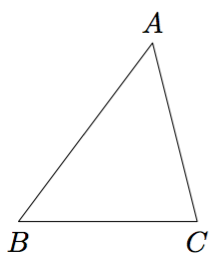
Suorakulmainen kolmio tarkoittaa kolmiota, jossa on suora kulma eli 90 asteen kulma. Yksi suorakulmainen kolmio on kuvattuna alla.
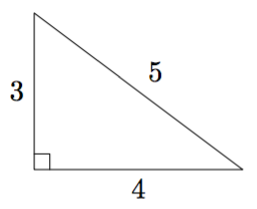
Suorakulmaisen kolmion pisintä sivua sanotaan hypotenuusaksi ja lyhyitä sivuja kateeteiksi. Yllä olevan suorakulmaisen kolmion hypotenuusan pituus on 5 ja kateettien pituudet ovat 3 ja 4.
Suorakulmaisen kolmion hypotenuusan pituus ja kateettien pituudet liittyvät toisiinsa niin sanotun Pythagoraan lauseen kautta:
TEOREEMA
Suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö, eli alla olevan kuvan merkinnöillä $$a^2 + b^2 = c^2$$

Seuraavissa tehtävissä harjoitellaan Pythagoraan lauseen soveltamista.
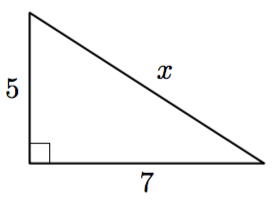
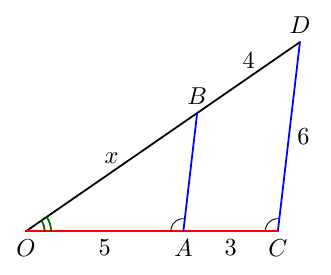
Tehtävänä on selvittää yllä olevan kolmion hypotenuusan pituus.
- Muodosta kolmion sivujen pituuksien välille Pythagoraan lauseen mukainen yhtälö. Ratkaise tästä yhtälöstä tuntemattoman sivun pituuden neliö eli $x^2$.
- Edellisessä kohdassa olet päätynyt toisen asteen yhtälöön $x^2 = s$, joita ratkaistiin kurssilla MAB2. Jos vakio $s$ on positiivinen eli $s > 0$, tällä yhtälöllä on kaksi ratkaisua. Mitkä nämä ratkaisut ovat a-kohdan yhtälön tapauksessa? Selitä omin sanoin, miksi vain toinen niistä voi olla kysytty kolmion sivun pituus.
- Mikä on yllä olevan kolmion hypotenuusan pituus? Anna vastauksen tarkka arvo ja likiarvo kahden merkisevän numeron tarkkuudella.
- $x^2 = 5^2 + 7^2$ eli $x^2 = 74$
- Ratkaisut ovat $x_1 = \sqrt{74}$ ja $x_2 = -\sqrt{74}$. Hypotenuusan pituus ei voi olla negatiivinen, joten vain positiivinen ratkaisu kelpaa.
- $x = \sqrt{74} \approx 8{,}6$.
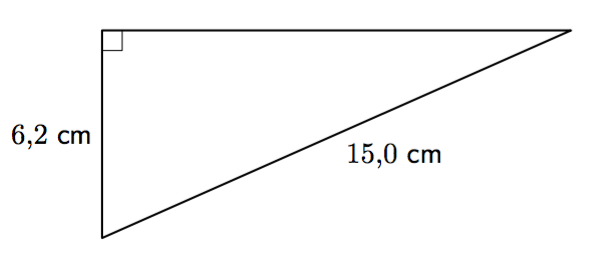
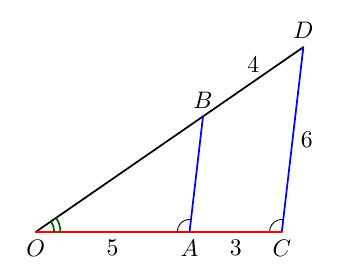
Tehtävänä on selvittää yllä olevan kolmion tuntemattoman sivun pituus.
- Merkitse tuntemattoman sivun pituutta jollakin kirjaimella. Muodosta kolmion sivujen pituuksien välille Pythagoraan lauseen mukainen yhtälö. Ratkaise tästä yhtälöstä tuntemattoman sivun pituuden neliö.
- Edellisessä kohdassa olet päätynyt toisen asteen yhtälöön. Ratkaise tästä yhtälöstä tuntemattoman sivun pituus. Anna vastaus kahden merkisevän numeron tarkkuudella.
- Pythagoraan lauseen mukainen yhtälö on $x^2 + 6{,}2^2 = 15{,}0^2$. Tästä saadaan $x^2 = 186{,}56$.
- Kolmion kolmannen sivun pituus on noin 14 cm. Tulos saadaan neliöjuuren avulla: $x = \sqrt{186{,}56} \approx 13{,}66$. Huomaa, että negatiivinen ratkaisu $x = -\sqrt{186{,}56}$ ei kelpaa, koska kysymyksessä on kolmion sivun pituus.
Seuraavan pohdintatehtävän ratkaisu osoittaa, että Pythagoraan lause pätee mille tahansa suorakulmaiselle kolmiolle.
- Neljä samanlaista suorakulmaista kolmiota asetellaan neliön muotoon kuten alla olevassa kuvassa. Miten voidaan päätellä, että keskelle jäävän valkoisen nelikulmion kaikki kulmat ovat suoria kulmia?
Vihje: kolmion kulmien summa (teoreema 2).
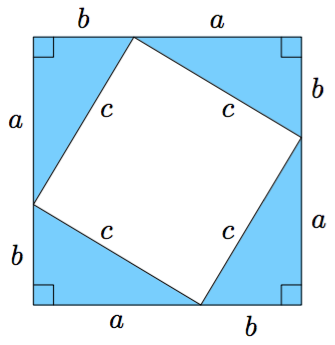
- Muodosta lauseke ylläolevan valkoisen neliön pinta-alalle.
- Samat suorakulmaiset kolmiot järjestetään uudelleen kuten alla olevassa kuvassa. Muodosta lauseke valkoisen alueen pinta-alalle.
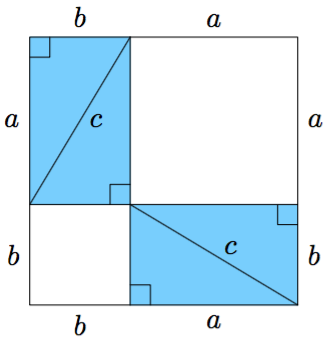
- Vertaa b- ja c-kohtien tuloksia. Millaisen yhtälön saat suorakulmaisen kolmion kateettien pituuksien ja hypotenuusan pituuden välille?
-
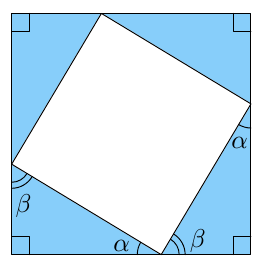
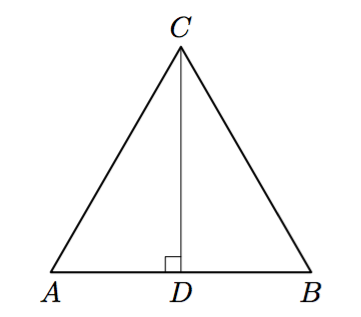
Kolmion kulmien summa on $180^\circ$, joten yhdestä pienestä suorakulmaisesta kolmiosta voidaan päätellä, että $$\alpha + \beta + 90^\circ = 180^\circ.$$ Tästä seuraa, että $$ \alpha + \beta = 90^\circ. $$ Valkoisen nelikulmion kulma muodostaa oikokulman yhdessä kulmien $\alpha$ ja $\beta$ kanssa. Valkoisen nelikulmion kulma on siis $$ 180^\circ - (\alpha + \beta) = 90^\circ. $$ - Valkoisen neliön pinta-ala on $c^2$.
- Valkoisen alueen pinta-ala on $a^2 + b^2$.
- Valkoisen alueen pinta-alan suuruus ei muutu, joten saadaan yhtälö $$ a^2 + b^2 = c^2. $$
Pythagoraan lausetta voidaan käyttää erilaisten arkipäiväistenkin ongelmien selvittämiseen. Seuraavissa tehtävissä on tästä kaksi esimerkkiä.
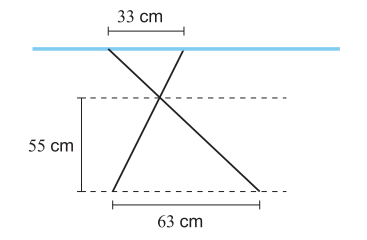
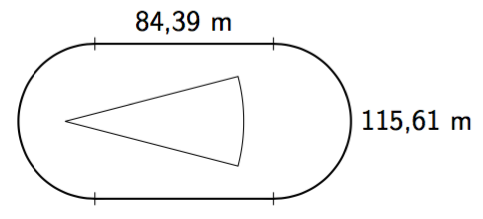
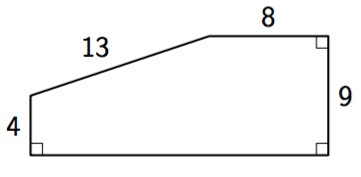
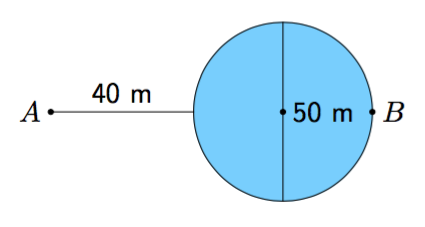
Puiston reunassa on kävelytie oheisen kuvan mukaisesti. Pisteestä $A$ pisteeseen $B$ pääsee myös oikopolkua suoraan metsän läpi. Oikopolku on merkitty kuvaan katkoviivalla.
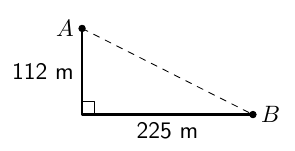
- Kuinka monta prosenttia lyhyemmän matkan oikopolkua käyttävä henkilö kulkee verrattuna kävelytietä kulkevaan?
- Henkilöt X ja Y lähtevät yhtä aikaa pisteestä $A$ kohti pistettä $B$. Henkilö X kulkee ripeästi kävelytietä vauhdilla 9 min/km ja henkilö Y oikaisee metsäpolun kautta rauhallisempaa 11 min/km vauhtia. Kuinka monta minuuttia heillä kuluu matkaan? Kumpi on aikaisemmin perillä?
- Noin 25,4 % lyhyemmän matkan. (Oikopolun pituus noin 251,3 metriä, kävelytien kokonaispituus 337 metriä.)
- Henkilö Y on aikaisemmin perillä, sillä hänellä kuluu matkaan noin 2,76 minuuttia eli 2 min 46 s. Henkilöllä X matkaan kuluu noin 3 minuuttia. (Häneltä kuluisi yhteen kilometriin 9 min, joten 337 metrin matkaan häneltä kuluu $$\dfrac{337}{1000} \cdot 9 = 3{,}033$$ minuuttia.)
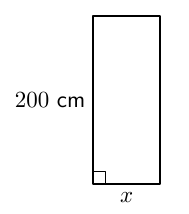
Hissin oviaukon korkeus on 2,00 metriä ja hissikorin pituus oviaukosta peräseinään on 1,40 metriä. Tehtävänä on selvitää, mikä hissin oven leveyden pitäisi vähintään olla, jotta 2,30 m pitkä ja 1,20 metriä leveä kipsilevy mahtuisi hissiin.
- Piirrä kuva hissin oviaukosta edestäpäin katsottuna. Merkitse piirrokseen oviaukon mitat. Merkitse oviaukon leveyttä jollakin kirjaimella.
- Missä asennossa kipsilevy kannattaa siirtää hissiin? Täydennä piirrosta ja merkitse siihen kipsilevyn mitta.
- Muodosta sopiva yhtälö ja ratkaise hissin oven leveys. Mikä on järkevä tarkkuus vastaukselle?
-
-
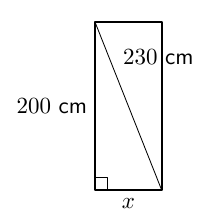
- Yhtälö on $$ 2^2 + x^2 = 2{,}3^2 $$ Oven vähimmäisleveys on $\sqrt{1{,}29} \text{ m} \approx 1{,}14 \text{ m}$. Vastaus kannattaa antaa senttimetrin tarkkuudella kuten lähtöarvotkin.
Pythagoraan lauseen avulla saadaan aina ratkaistua suorakulmaisen kolmion kolmas sivu, jos kahden sivun pituus tunnetaan. Sivujen pituuksien avulla voidaan puolestaan selvittää suorakulmaisen kolmion terävien kulmien suuruus. Apuna käytetään sivujen pituuksien suhteita, jotka on nimetty seuraavasti:
MÄÄRITELMÄ: SINI, KOSINI JA TANGENTTI
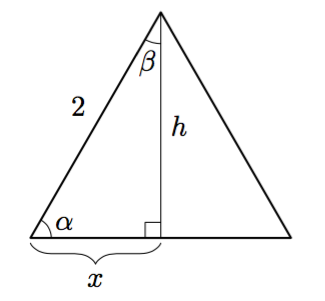
Suorakulmaisessa kolmiossa terävän kulman $\alpha$ sini, kosini ja tangetti tarkoittavat kolmion sivujen pituuksien suhteita: \begin{align*} \sin \alpha &= \dfrac{\text{ kulman vastainen kateetti }}{\text{ hypotenuusa }} \\[2mm] \cos \alpha &= \dfrac{\text{ kulman viereinen kateetti }}{\text{ hypotenuusa }} \\[2mm] \tan \alpha &= \dfrac{\text{ kulman vastainen kateetti }}{\text{ kulman viereinen kateetti }} \end{align*}
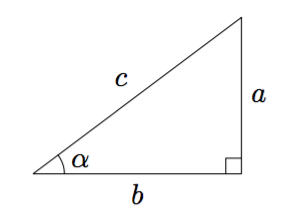
Yllä olevan kuvion merkinnöillä \begin{align*} \sin \alpha &= \dfrac{a}{c} \\[1mm] \cos \alpha &= \dfrac{b}{c} \\[1mm] \tan \alpha &= \dfrac{a}{b} \end{align*}
Kulman sini on siis luku, joka ilmaisee, miten pitkä kulman vastainen kateetti on hypotenuusaan verrattuna. Vastaavasti kulman kosini ilmaisee, miten pitkä kulman viereinen kateetti on hypotenuusaan verrattuna. Seuraavassa tehtävässä lasketaan näitä pituuksien suhteita yhden kolmion tapauksessa.
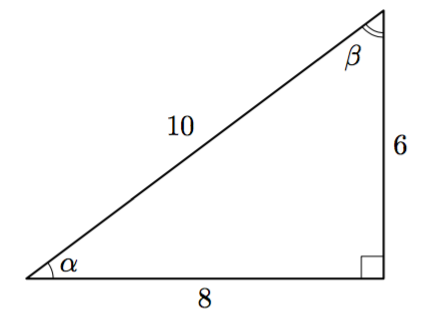
Suorakulmaisen kolmion hypotenuusan pituus on 10 ja kateettien pituudet ovat 6 ja 8 yllä olevan kuvan mukaisesti. Määritä seuraavat sivujen suhteet:
- $\sin \alpha$
- $\cos \alpha$
- $\tan \alpha$
- $\sin \beta$
- $\cos \beta$
- $\tan \beta$
Anna vastaukset supistettuina murtolukuina ja desimaalilukumuodossa.
- $\sin \alpha = \dfrac{3}{5} = 0{,}6$
- $\cos \alpha = \dfrac{4}{5} = 0{,}8$
- $\tan \alpha = \dfrac{3}{4} = 0{,}75$
- $\sin \beta = \dfrac{4}{5} = 0{,}8$
- $\cos \beta = \dfrac{3}{5} = 0{,}6$
- $\tan \beta = \dfrac{4}{3} \approx 1{,}33$
Jos trigonometrisen suhteen arvo tiedetään, voidaan sen avulla muodostaa esimerkki vastaavasti suorakulmaisesta kolmiosta. Esimerkiksi jos $$ \sin \alpha = \dfrac{4}{9} $$ niin yksi esimerkki vastaavasta suorakulmaisesta kolmiosta on sellainen, jossa hypotenuusan pituus on 9 ja kulman $\alpha$ vastaisen kateetin pituus on 4. Kolmion kolmannen sivun pituus saadaan selville Pythagoraan lauseella.
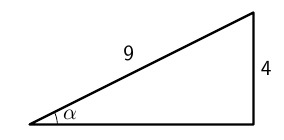
Suorakulmaisessa kolmiossa terävän kulman $\alpha$ tangetti on $5:12$ eli $$\tan \alpha = \frac{5}{12}$$
- Keksi esimerkki suorakulmaisesta kolmiosta, jossa on tällainen terävä kulma. Mitkä ovat keksimäsi suorakulmaisen kolmion kateettien pituudet?
- Laske keksimäsi suorakulmaisen kolmion hypotenuusan pituus.
- Keksi esimerkki toisesta suorakulmaisesta kolmiosta, jossa on samanlainen kulma $\alpha$. Selitä omin sanoin, miten ajattelit.
- Esimerkiksi kolmio, jonka kateettien pituudet ovat 5 ja 12.
- Hypotenuusan pituus saadaan yhtälöstä $$ x^2 = 5^2 + 12^2. $$ Hypotenuusan pituus on 13.
- Esimerkiksi kolmio,jonka kateettien pituudet ovat 10 ja 24. Kasvatetaan kolmion kaikkien sivujen pituudet kaksinkertaisiksi, jolloin kolmion sivujen suhteet pysyvät samoina.
Jossain tapauksissa on mahdollista päätellä kuviosta sekä kulman suuruus että sen sinin, kosinin ja tangentin arvot. Yksi esimerkki tällaisesta tilanteesta on seuraavassa tehtävässä.
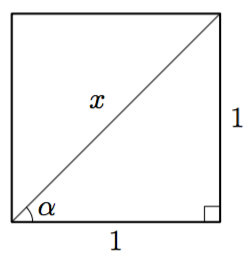
Tarkastele alla olevaa neliötä, joka on jaettu lävistäjällä kahdeksi suorakulmaiseksi kolmioksi.
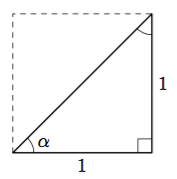
- Laske suorakulmaisen kolmion hypotenuusan pituus.
- Päättele kulman $\alpha$ suuruus kolmion symmetrian avulla.
Vihje: teoreema 2. - Määritä kolmion sivujen pituuksien avulla $\sin \alpha$, $\cos \alpha$ ja $\tan \alpha$.
- Hypotenuusan pituus saadaan yhtälöstä $$ x^2 = 1^2 + 1^2. $$ Hypotenuusan pituus on $x = \sqrt{2}$.
- Kolmion kulmien summa on $$ \alpha + \alpha + 90^\circ = 180^\circ. $$ Tästä saadaan $2\alpha = 90^\circ$ eli $\alpha = 45^\circ$.
- $\sin \alpha = \dfrac{1}{\sqrt{2}}$, $\cos \alpha = \dfrac{1}{\sqrt{2}}$ ja $\tan \alpha = 1$.
Edellisen tehtävän perusteella voidaan laatia seuraava taulukko:
| Kulma $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ |
| $45^\circ$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{\sqrt{2}}$ | $1$ |
Jokaista terävää kulmaa vastaa yksi sinin, kosinin ja tangentin arvo. Esimerkiksi yllä olevasta taulukosta nähdään, että $$\cos 45^\circ = \dfrac{1}{\sqrt{2}}.$$
Toisaalta jokaista (suorakulmaisessa kolmiossa mahdollista) trigonometristä suhdetta vastaa yksi terävä kulma. Esimerkiksi yllä olevan taulukon avulla voidaan päätellä, että jos $\tan \beta = 1$, niin $\beta = 45^\circ$.
Laskinten ja tietokoneiden avulla tämä siirtyminen kulman ja trigonometristen suhteiden välillä voidaan tehdä ilman taulukoiden käyttöä. Annettua kulmaa vastaava trigonometrinen suhde sini, kosini tai tangentti saadaan laskimella käyttämällä nappulaa $\bbox[3px,border:2px solid black]{\texttt{sin}\phantom{i}}\ $, $\ \bbox[3px,border:2px solid black]{\texttt{cos}\phantom{i}}\ $ tai $\ \bbox[3px,border:2px solid black]{\texttt{tan}\phantom{i}}\ $. Trigonometrista suhdetta vastaava kulma saadaan nappuloilla $\bbox[3px,border:2px solid black]{\texttt{sin}^{-1}}\ $, $\ \bbox[3px,border:2px solid black]{\texttt{cos}^{-1}}\ $ ja $\ \bbox[3px,border:2px solid black]{\texttt{tan}^{-1}}\ $.
Siirtymistä kulman ja trigonometristen suhteiden välillä kumpaankin suuntaan harjoitellaan seuraavassa tehtävässä.
Kopioi alla oleva taulukko vihkoosi ja täydennä siihen puuttuvat tiedot laskimen avulla tarkkoina arvoina tai kolmen merkitsevän numeron tarkkuudella:
| Kulma $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ |
| $10^\circ$ | $\phantom{\dfrac{1}{2}}$ | | |
| | $\dfrac{1}{2}$ | | |
| | | $\dfrac{1}{\sqrt{2}}$ | |
| | $\phantom{\dfrac{1}{2}}$ | | $\sqrt{3}$ |
| $80^\circ$ | $\phantom{\dfrac{1}{2}}$ | | |
Löydätkö taulukosta kulmia, joiden summa on $90^\circ$? Vertaa tällaisten kulmien sinejä ja kosinejä toisiinsa. Mitä havaitset?
| Kulma $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ |
| $10^\circ$ | $0{,}174$ | $0{,}985$ | $0{,}176$ |
| $30^\circ$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{3}}$ |
| $45^\circ$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{\sqrt{2}}$ | $1$ |
| $60^\circ$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{2}$ | $\sqrt{3}$ |
| $80^\circ$ | $0{,}985$ | $0{,}174$ | $5{,}67$ |
Taulukosta nähdään, että jos $\alpha + \beta = 90^\circ$, niin $\sin \alpha = \cos \beta$ ja $\cos \alpha = \sin \beta$.
Seuraavissa tehtävissä harjoitellaan selvittämään suorakulmaisen kolmion tuntemattomat sivujen pituudet ja kulmat trigonometristen suhteiden ja Pythagoraan lauseen avulla. Kolmion kulmien summa (teoreema 2) on sekin hyödyllinen tieto.
Tarkastele alla olevaa suorakulmaista kolmiota.
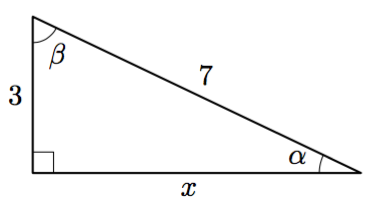
- Selvitä toisen kateetin pituus (tarkka arvo).
- Selvitä kulman $\alpha$ suuruus jonkin trigonometrisen suhteen avulla. Anna vastaus kolmen merkitsevän numeron tarkkuudella.
- Selvitä kulman $\beta$ suuruus.
- $\sqrt{40} = 2\sqrt{10}$
- $\alpha \approx 25{,}4^\circ$
- $\beta \approx 64{,}6^\circ$
Tarkastele alla olevaa suorakulmaista kolmiota.
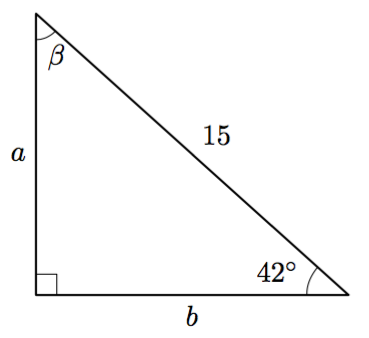
- Ilmaise $\sin 42^\circ$ kolmion sivujen suhteena. Ratkaise tästä yhtälöstä kateetin $a$ pituus kolmen merkitsevän numeron tarkkuudella.
- Ilmaise $\cos 42^\circ$ kolmion sivujen suhteena. Ratkaise tästä yhtälöstä kateetin $b$ pituus kolmen merkitsevän numeron tarkkuudella.
- Selvitä kulman $\beta$ suuruus.
- $a \approx 10{,}0$
- $b \approx 11{,}1$
- $\beta = 48^\circ$
Seuraavassa tehtävässä käytetään trigonometrisia suhteita mäen kaltevuuskulman selvittämiseen. Tieliikenteessä poikkeuksellisen jyrkistä mäistä varoitetaan omalla varoitusmerkillään.
Laskettelurinteen pituus on 1300 metriä ja korkeusero 262 metriä. Tehtävänä on laskea mäen rinteen keskimääräinen kaltevuuskulma (vaakatasoon verrattuna).
- Piirrä mallikuva, jossa rinteen poikkileikkaus sivusta katsottuna on suorakulmainen kolmio. Merkitse kuvaan rinteen mitat.
- Ratkaise rinteen kaltevuuskulma sopivan trigonometrisen suhteen avulla. Anna vastaus kahden merkitsevän numeron tarkkuudella.
-
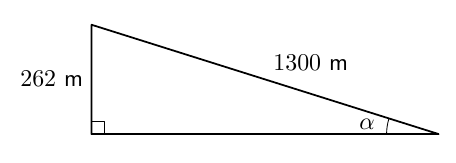
- Rinteen kaltevuuskulma on noin 12 astetta. Vastaus löydetään esimerkiksi ratkaisemalla yhtälö $$ \sin \alpha = \dfrac{262}{1300}. $$
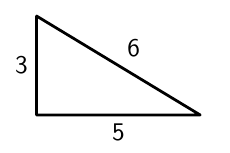
Tässä kappaleessa on opiskeltu suorakulmaisen kolmion geometriaa. Kaikista kolmioista ei kuitenkaan pysty silmämääräisesti näkemään, ovatko ne suorakulmaisia vai eivät. Miten esimerkiksi voidaan selvittää, onko alla oleva kolmio suorakulmainen vai ei?
Asian selvittämiseen voidaan käyttää niin sanottua Pythagoraan lauseen käänteislausetta:
TEOREEMA
Jos kolmion sivun pituudet toteuttavat yhtälön $$ a^2 + b^2 = c^2 $$ niin kolmio on suorakulmainen.

Esimerkin kolmion kateettien neliöiden summaksi saadaan $$ 3^2 + 5^2 = 9 + 25 = 34. $$ Tämä on erisuuri kuin hypotenuusan neliö $6^2 = 36$, joten $a^2 + b^2 \neq c^2$. Kolmio ei siis ole suorakulmainen, vaikka se silmämääräisesti sellaiselta saattaa näyttääkin.
Tutki, ovatko seuraavat kolmiot suorakulmaisia:
- Kolmio, jonka sivujen pituudet ovat 60 mm, 91 mm ja 109 mm.
-
- Kolmio on suorakulmainen, sillä kateettien neliöiden summa on hypotenuusan neliö: $$ 60^2 + 91^2 = 11881 = 109^2. $$
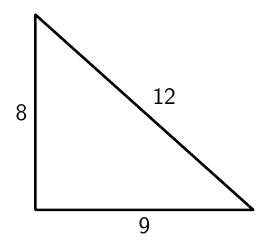
- Kolmio ei ole suorakulmainen, sillä kateettien neliöiden summa on erisuuri kuin hypotenuusan neliö: $$ 8^2 + 9^2 = 145 \neq 144 = 12^2. $$



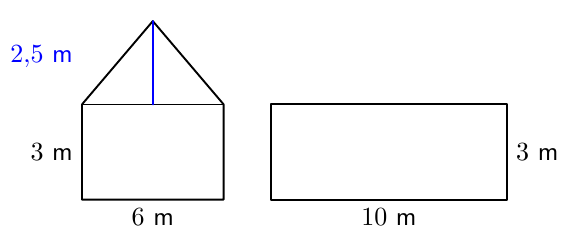
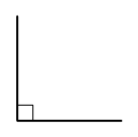
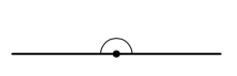
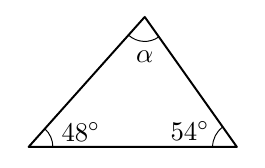











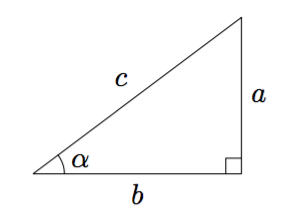















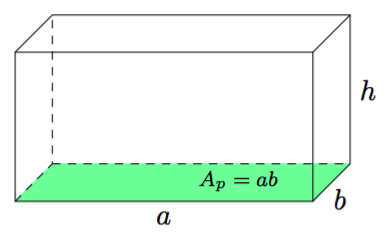
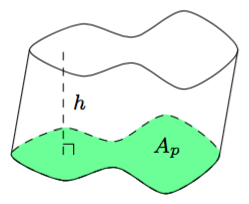
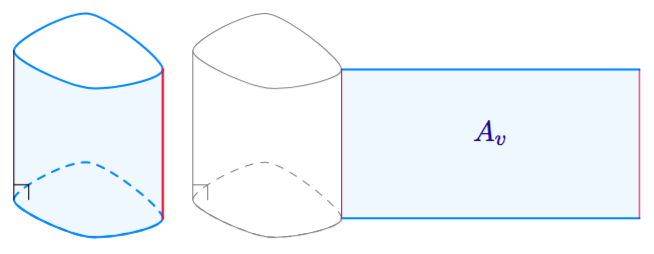
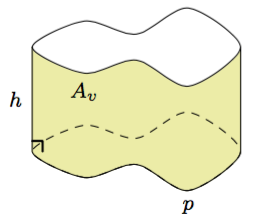
 Sovitaan seuraavaksi vielä tarkemmin, mitä tarkoitetaan suorakulmaisella särmiöllä.
Sovitaan seuraavaksi vielä tarkemmin, mitä tarkoitetaan suorakulmaisella särmiöllä. 
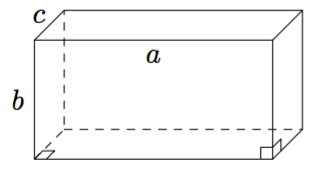
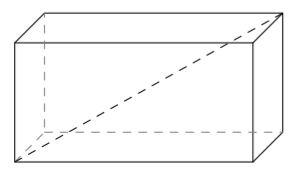
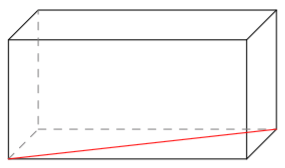
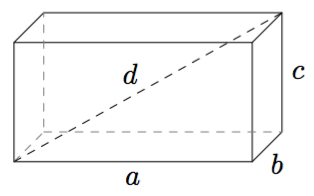

 (Yllä olevat punaiset kuvat Robert Webb,
(Yllä olevat punaiset kuvat Robert Webb,