Tässä luvussa tutustutaan matematiikkaan, jota suuri osa ihmisistä käyttää arkipäiväisessä elämässään kiinnittämättä asiaan kovin paljon huomioita. Seuraavassa tehtävässä on yksi tällainen tilanne. Voit ratkaista tehtävän esimerkiksi arkijärjellä päättelemällä tai jollakin muulla sinulle luontevalla tavalla.
Kuivattujen päärynöiden hinta on 1,49 € / 100 g. Kuinka paljon maksaa 285 g kuivattuja päärynöitä?
Tutkitaan seuraavaksi, millaista matematiikkaa edelliseen tehtävään liittyy. Tehtävässä tarkasteltiin kahta suuretta: hintaa ja massaa. Luvussa 1 opittiin, että suure tarkoittaa ominaisuutta, joka voidaan mitata tai laskea tai muuten määrittää. Suure ilmaistaan lukuarvon ja yksikön avulla: päärynöiden massa on 285 g.
Jos suureilla on sama yksikkö, niitä voidaan verrata muodostamalla niiden suhde eli osamäärä. Esimerkiksi voidaan verrata päärynöiden massoja: $$ \dfrac{285 \text{ g}}{100 \text{ g}} = 2{,}85. $$ Päärynöiden hinta on ilmaistu sanomalla, että 100 grammaa maksaa 1,49 €. Yllä olevan suhteen mukaan massa 285 g on siihen verrattuna 2,85-kertainen, joten hintakin on 2,85-kertainen. Siis 285 g päärynöitä maksaa $$ 2{,}85 \cdot 1{,}49 \ \euro = 4{,}2465 \ \euro \approx 4{,}25 \ \euro. $$
Vertaa yllä esitettyä ratkaisutapaa ja omaa päättelyäsi tehtävässä 3.1. Mitä yhteistä niissä on? Entä mitä eroja niissä on? Selitä omin sanoin.
Kuivattujen päärynöiden hinta on 1,49 € / 100 g. Kuinka paljon kuivattuja päärynöitä saa viidellä eurolla?
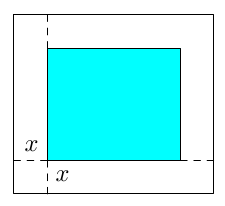
Usein tehtävän ratkaisu helpottuu, jos kokoaa kaikki tehtävässä annetut tiedot sopivaan taulukkoon. Kysyttä asiaa voi merkitä kirjaimella $x$. Esimerkiksi yllä olevan tehtävän tilanteessa taulukko voisi näyttää tältä:
| | Määrä (g) | Hinta (€) |
| Asiakkaalla | $x$ | 5,00 |
| Hintalapussa | 100 | 1,49 |
Taulukosta saadaan muodostettua kaksi suhdetta: päärynöiden määrän suhde ja päärynöiden hinnan suhde. Jos päärynöiden määrä esimerkiksi kaksinkertaistuu, myös hinta kaksinkertaistuu. Vaikka suureet muuttuvat, niiden suhteet pysyvät samana. Saadaan yhtälö $$ \dfrac{x}{100} = \dfrac{5{,}00}{1{,}49}. $$ Tällainen yhtälö, jossa kaksi suhdetta on merkitty yhtä suuriksi, on nimeltään verranto. Kysytty päärynöiden määrä saadaan selville, kun verrannon molemmat puolet kerrotaan sadalla: \begin{align*} \dfrac{x}{100} &= \dfrac{5{,}00}{1{,}49} \quad \mid \ \cdot 100\\[1mm] x &= \dfrac{100 \cdot 5{,}00}{1{,}49} \approx 335{,}57 \end{align*} Viidellä eurolla saadaan siis noin 336 grammaa kuivattuja päärynöitä. Tarkasti ottaen tässä pyöristyksen voi tehdä alaspäin: jos käytettävissä on enintään 5,00 euroa, riittää se 335 grammaan päärynöitä, mutta 336 grammaa maksaa jo hiukan liikaa.
Vertaa yllä esitettyä ratkaisutapaa ja omaa päättelyäsi tehtävässä 3.2. Mitä yhteistä niissä on? Entä mitä eroja niissä on? Selitä omin sanoin.
Päärynöiden määrän ja hinnan välistä riippuvuutta voidaan kuvata ja tutkia myös graafisesti. Tähän perehdytään seuraavassa tehtävässä.
Tässä tehtävässä tutkitaan päärynöiden määrän ja hinnan välistä riippuvuutta graafisesti eli kuvan avulla.
- Tiedetään, että 100 g kuivattuja päärynöitä maksaa 1,49 €. Täytä tämän tiedon avulla seuraava taulukko:
| Määrä (g) | Hinta (€) |
| 0 | |
| 100 | 1,49 |
| 200 | |
| 300 | |
| 400 | |
| 500 | |
| 600 | |
| 700 | |
| 800 | |
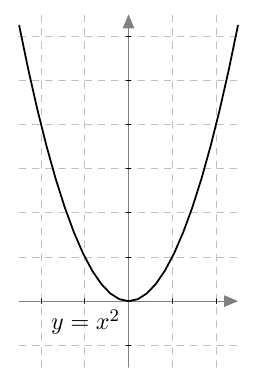
- Jokainen taulukon rivi vastaa koordinaatiston pistettä. Esimerkiksi yksi piste on $(100; 1{,}49)$. Piirrä samanlainen koordinaatisto kuin alla ja merkitse kaikki muutkin pisteet siihen. Millainen kuvio pisteistä muodostuu?
- Miten saisit b-kohdan kuvan avulla selvitettyä, kuinka paljon maksaa 650 g kuivattuja päärynöitä? Selitä omin sanoin ja piirroksin.
- Miten saisit b-kohdan kuvan avulla selvitettyä, kuinka paljon kuvattuja päärynöitä saa 7 eurolla? Selitä omin sanoin ja piirroksin.
- Taulukko:
| Määrä (g) | Hinta (€) |
| 0 | 0 |
| 100 | 1,49 |
| 200 | 2,98 |
| 300 | 4,47 |
| 400 | 5,96 |
| 500 | 7,45 |
| 600 | 8,94 |
| 700 | 10,43 |
| 800 | 11,92 |
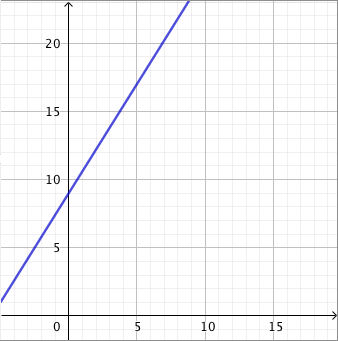
- Pisteet asettuvat suoralle:
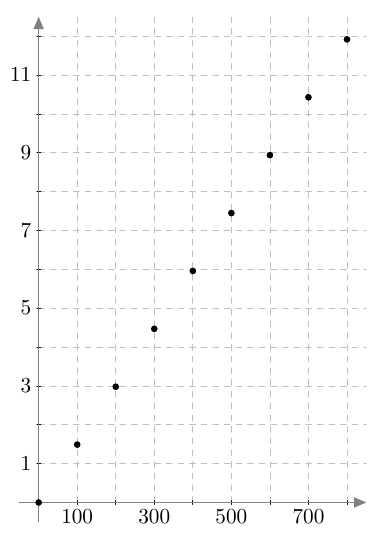
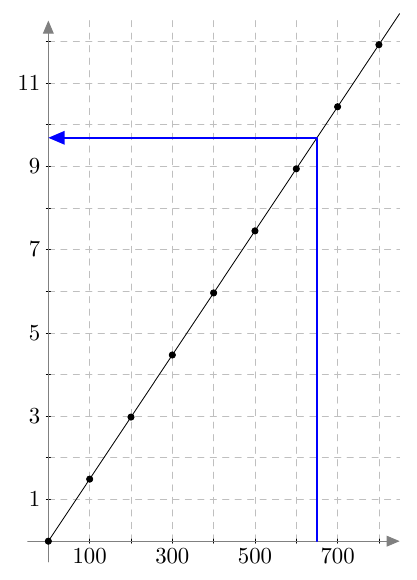
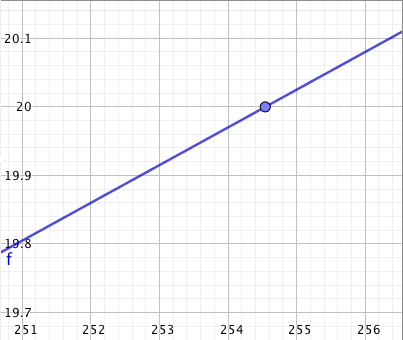
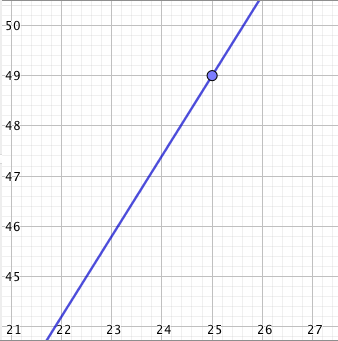
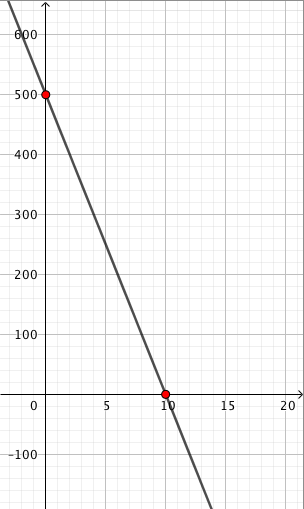
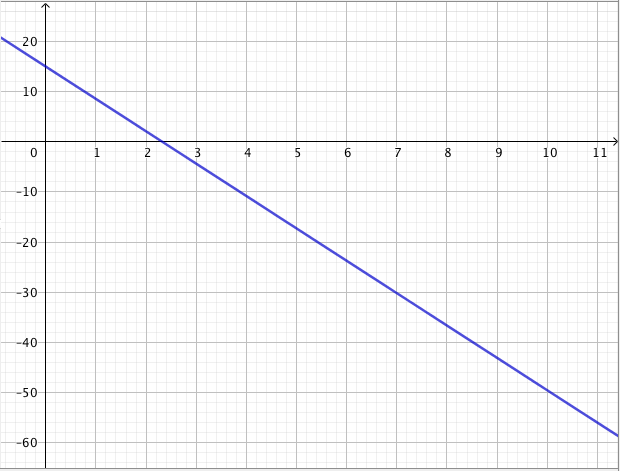
- Piirretään suora näkyviin ja katsotaan, mikä suoran pisteen $y$-koordinaatti on kohdassa $x = 650$. Havaitaan, että 650 g päärynöitä maksaa noin 9,7 euroa:
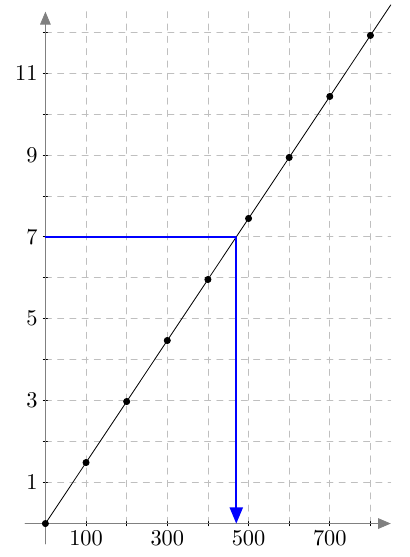
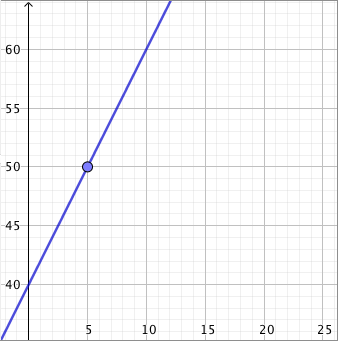
- Piirretään suora näkyviin ja katsotaan, missä kohdassa suoran pisteen $y$-koordinaatti on $y = 7$. Havaitaan, 7 eurolla saa noin 470 grammaa päärynöitä:
Edellisessä tehtävässä havaittiin, että päärynöiden määrän ja hinnan välistä riippuvuutta voidaan kuvata origon kautta kulkevalla suoralla. Tämä havainto voidaan ottaa lähtökohdaksi, kun sovitaan, mitä tarkoitetaan suoraan verrannollisilla suureilla.
MÄÄRITELMÄ: SUORAAN VERRANNOLLISUUS
Suureet $x$ ja $y$ ovat suoraan verrannolliset, jos niiden välinen riippuvuus voidaan kuvata yhtälöllä $$y = kx.$$ Vakio $k$ on verrannollisuuskerroin.
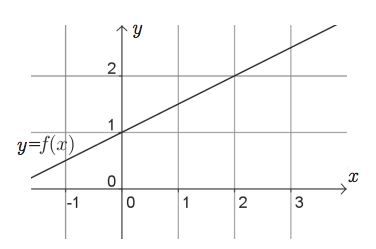
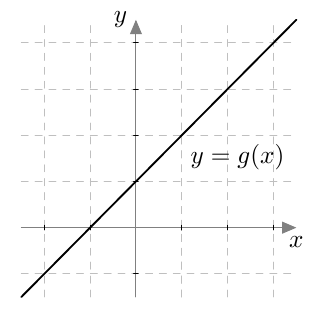
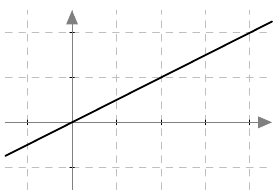
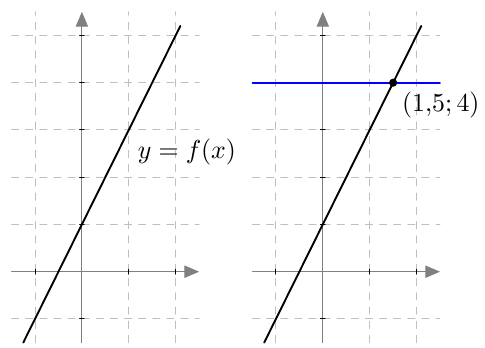
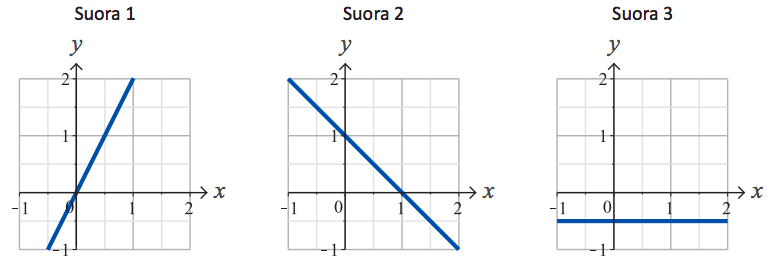
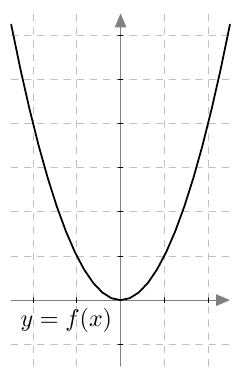
Yleensä verrannollisuuskerroin $k$ on positiivinen, jolloin suoraan verrannollisuutta kuvaa nouseva suora:
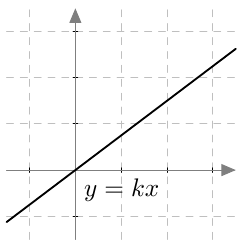
Kuvasta nähdään, että suoraan verrannolliset positiiviset suureet muuttuvat samaan suuntaan: jos suureen $x$ arvo kasvaa (eli liikutaan $x$-akselia oikealle), myös suureen $y$ arvo kasvaa (eli liikutaan $y$-akselia ylöspäin). Suureiden välinen suhde on kuitenkin koko ajan vakio: yhtälöstä $$y = kx$$ seuraa, että $$ \dfrac{y}{x} = k. $$ Suoraan verrannolliset suureet muuttuvat siis samassa suhteessa: Jos toinen vaikkapa kolminkertaistuu, myös toinen kolminkertaistuu. Suureiden suhde pysyy samana.
Jos suureet ovat suoraan verrannolliset, voidaan tuntemattomia arvoja selvittää verrannon avulla kuten jo aiemmin tehtiin. Käytännössä suoraan verrannolliset suureet tunnistetaan, kun mietitään arkijärjellä, kasvavatko suureet samassa suhteessa. Tämän voi tehdä esimerkiksi miettimällä, mitä toiselle suureelle tapahtuu, jos toinen kaksinkertaistuu. Jos toisen suureen kaksinkertaistuessa myös toinen suure kaksinkertaistuu, ovat suureet suoraan verrannolliset.
Leirille osallistuu 26 henkeä. Aamupalalla tarjoillaan kaurapuuroa. Kaurahiutalepaketin ohjeen mukaan neljän hengen annokseen laitetaan 5 dl kaurahiutaleita ja 1,25 litraa vettä. Tehtävänä on selvittää, kuinka monta 500 g kaurahiutalepakettia leiriä varten pitää ostaa, kun leiri kestää kolme vuorokautta. Kaurahiutalepaketin kyljestä nähdään, että 1 dl kaurahiutaleita painaa n. 35 grammaa.
- Tunnista tehtävästä kaksi suuretta, jotka ovat suoraan verrannollisia. Keksitkö vielä kaksi muuta suuretta, jotka ovat suoraan verrannollisia? Selitä omin sanoin, miten päättelit niiden olevan suoraan verrannollisia.
- Selvitä, kuinka paljon kaurahiutaleita tarvitaan, kun puuroa keitetään 26 hengelle. Muodosta sopiva verranto ja ratkaise se. Voit käyttää apuna alla olevaa taulukkoa.
| | Hiutaleita (dl) | Ihmisiä |
| Leirillä | | |
| Paketin reseptissä | | |
- Ilmaise b-kohdan hiutalemäärä grammoina. Voit käyttää apuna alla olevaa taulukkoa ja sopivaa verrantoa.
| | Hiutaleita (dl) | Hiutaleita (g) |
| Aamiaisella | | |
| Paketin kyljessä | | |
- Kuinka paljon kaurahiutaleita kuluu koko leirin aikana? Kuinka monta 500 gramman pakettia kannattaa ostaa?
-
Suoraan verrannollisia ovat esimerkiksi ihmisten lukumäärä ja tarvittavien kaurahiutaleiden määrä. Nimittäin jos ihmisten määrä kaksinkertaistuu, tarvitaan myös kaurahiutaleita kaksinkertainen määrä.
Suoraan verrannollisia ovat myös esimerkiksi puuroon käytettävä kaurahiutaleiden määrä ja veden määrä. Jos toinen kaksinkertaistetaan, pitää toinenkin kaksinkertaistaa, jotta puuro onnistuu.
- Taulukko:
| | Hiutaleita (dl) | Ihmisiä |
| Leirillä | $x$ | 26 |
| Paketin reseptissä | 5 | 4 |
Saadaan verranto $$ \dfrac{x}{5} = \dfrac{26}{4}. $$ Ratkaisu on $x = 32{,}5$ dl. - Ilmaise a-kohdan hiutalemäärä grammoina. Voit käyttää apuna alla olevaa taulukkoa ja sopivaa verrantoa.
| | Hiutaleita (dl) | Hiutaleita (g) |
| Aamiaisella | 32,5 | $y$ |
| Paketin kyljessä | 1 | 35 |
Saadaan verranto $$ \dfrac{y}{35} = \dfrac{32{,}5}{1}. $$ Ratkaisu on $y = 1137{,}5$ g. Kun otetaan huomioon, että lähtötiedoissa on 2-3 merkitsevää numeroa, on tulos järkevää pyöristää samaan tarkkuuteen: yhtenä aamuna kuluu noin 1140 grammaa kaurahiutaleita. - Edellisen kohdan avulla voidaan arvioida, että koko leirin aikana kuluu noin $3 \cdot 1140 \text{ g} = 3420 \text{ g}$ kaurahiutaleita. Koska $$ \dfrac{3420 \text{ g}}{500 \text{ g}} = 6{,}84, $$ tarvitaan seitsemän 500 gramman pakettia. Tarkistus: $7 \cdot 500 \text{ g} = 3500 \text{ g}$ eli riittävästi.
Edellisessä tehtävässä selvitettiin kaurahiutaleiden määrä verrannon avulla, kun tiedetiin, että kaurahiutaleiden määrä ja ihmisten määrä ovat suoraan verrannollisia. Oikeanlaisen verrannon muodostamisessa kannattaa käyttää apuna taulukkoa:
| | Suure A | Suure B |
| Tilanne 1 | | |
| Tilanne 2 | | |
Taulukossa oleellista on, että kumpikin suure on omassa sarakkeessaan ja niiden arvot eri tilanteissa ovat johdonmukaisesti omilla riveillään. Tällöin taulukosta saadaan suoraan muodostettua sopiva verranto. Verrannon ratkaiseminen on helpointa, jos taulukon laatii niin, että kysytty asia on taulukon ylimmällä rivillä.
Laura pyöräilee 5,9 kilometrin matkan kirjastoon 22 minuutissa.
- Uimahalli on 8,2 km päässä. Kuinka kauan Lauran pyörämatka uimahallille kestää? Muodosta sopiva verranto taulukon avulla ja ratkaise se.
- Viikonloppuna Laura päättää pyöräillä kaverinsa luo. Matkan pituus on reittioppaan mukaan 13,3 km. Kuinka paljon aikaa Lauran kannattaa varata matkaan? Muodosta sopiva verranto taulukon avulla ja ratkaise se.
- Kumpi a- ja b-kohdan tuloksista mielestäsi paremmin ennustaa pyörämatkan todellista kestoa? Selitä omin sanoin, miten ja miksi matkan todellinen kesto voi poiketa lasketusta.
- Taulukko:
| | Aika (min) | Matka (km) |
| Uimahalli | $x$ | 8,2 |
| Kirjasto | 22 | 5,9 |
Saadaan verranto $$ \dfrac{x}{22} = \dfrac{8{,}2}{5{,}9}. $$ Ratkaisu on $$x = 22 \cdot \dfrac{8{,}2}{5{,}9} \approx 31$$ eli noin 31 minuuttia. - Taulukko:
| | Aika (min) | Matka (km) |
| Kaveri | $x$ | 13,3 |
| Kirjasto | 22 | 5,9 |
Saadaan verranto $$ \dfrac{x}{22} = \dfrac{13{,}3}{5{,}9}. $$ Ratkaisu on $$x = 22 \cdot \dfrac{13{,}3}{5{,}9} \approx 50$$ eli noin 50 minuuttia. - Voi ajatella, että a-kohdan tulos saattaa olla luotettavampi, koska lyhyemmällä matkalla jaksaa paremmin pitää saman nopeuden kuin kirjastoon ajaessa. Sääolosuhteet ja esimerkiksi liikennevalot voivat vaikuttaa molempien matkojen kestoon.
Auton jarrutusmatka on suoraan verrannollinen auton nopeuden neliöön eli toiseen potenssiin. Märällä tiellä mitattiin auton jarrutusmatkaksi 10 metriä, kun jarrutus aloitettiin 40 km/h nopeudesta.
- Selvitä, mikä olisi jarrutusmatka vastaavissa olosuhteissa, jos nopeus jarrutuksen alkaessa olisi 60 km/h. Käytä apuna alla olevaa taulukkoa.
| | Jarrutusmatka (m) | Nopeus2 (km2/h2) |
| Arvio | | |
| Mittaus | | |
- Tutki, miten jarrutusmatka pitenee, jos nopeus kaksinkertaistuu. Voit esimerkiksi valita sopivan nopeuden ja selvittää sitä vastaavan jarrutusmatkan samaan tapaan kuin a-kohdassa.
- Taulukko:
| | Jarrutusmatka (m) | Nopeus2 (km2/h2) |
| Arvio | $x$ | $60^2 = 3600$ |
| Mittaus | $10$ | $40^2 = 1600$ |
Saadaan verranto $$ \dfrac{x}{10} = \dfrac{3600}{1600}. $$ Ratkaisu on $$x = 10 \cdot \dfrac{36}{16} = 22{,}5$$ eli noin 23 metriä. - Voidaan käyttää nopeutta $$2 \cdot 40 \text{ km/h} = 80 \text{ km/h}.$$ Taulukko:
| | Jarrutusmatka (m) | Nopeus2 (km2/h2) |
| Arvio | $x$ | $80^2 = 6400$ |
| Mittaus | $10$ | $40^2 = 1600$ |
Saadaan verranto $$ \dfrac{x}{10} = \dfrac{6400}{1600}. $$ Ratkaisu on $$x = 10 \cdot \dfrac{64}{16} = 40.$$ Nopeuden kaksinkertaistuessa jarrutusmatka muuttuu 10 metristä 40 metriin eli nelinkertaistuu.

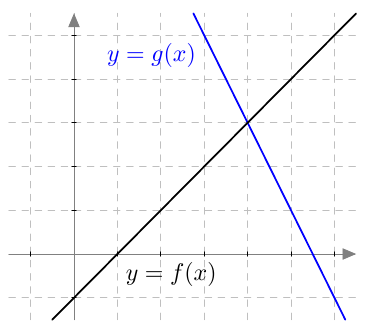
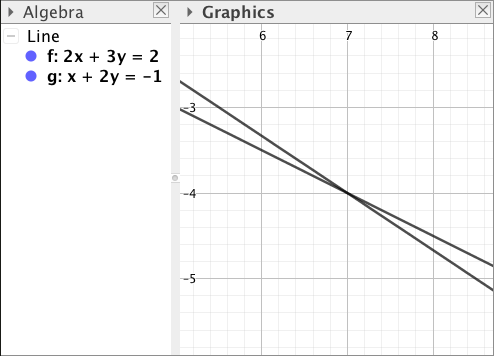
 Tarkistus:
Tarkistus: 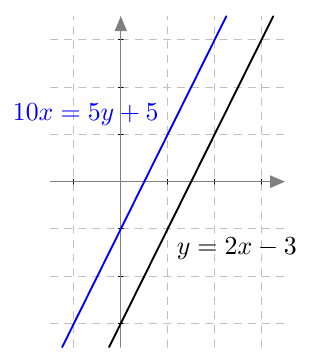
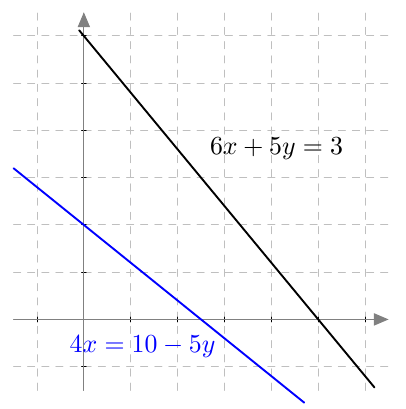
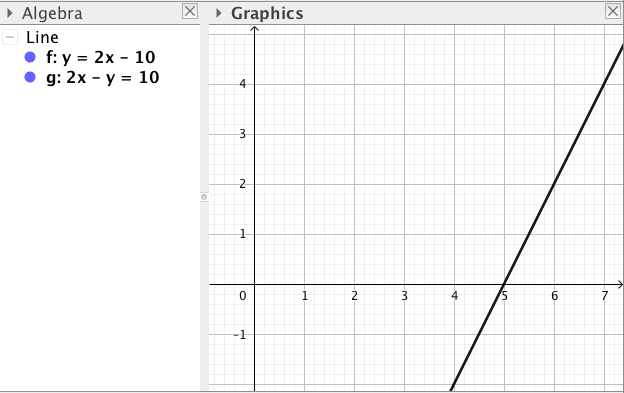
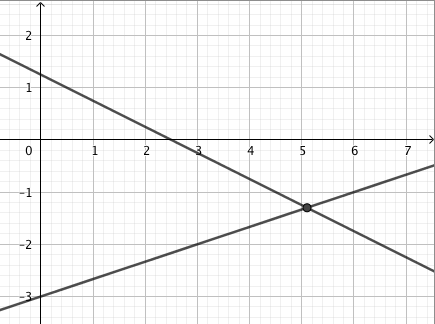
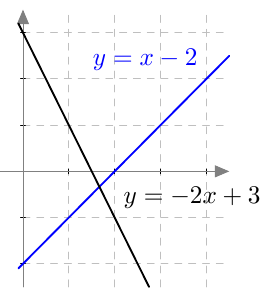
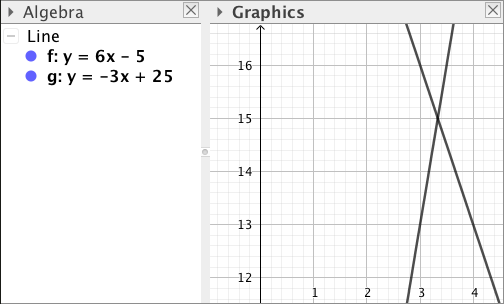
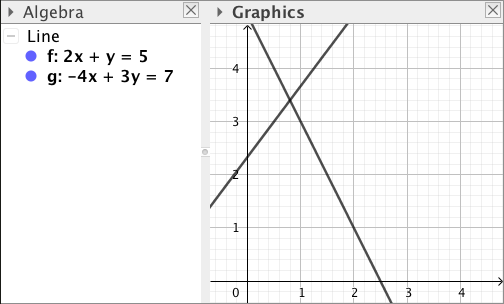
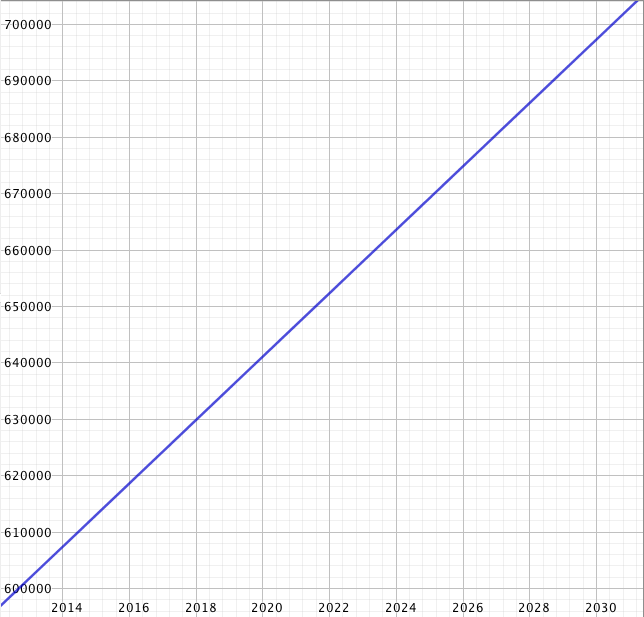




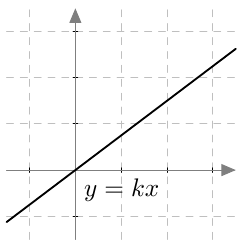
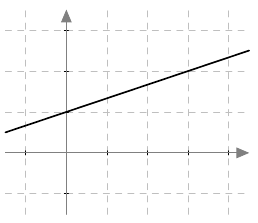
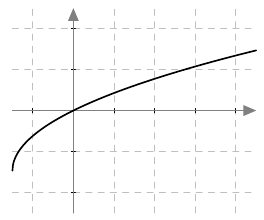
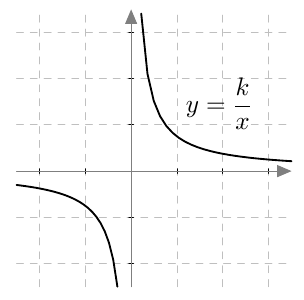
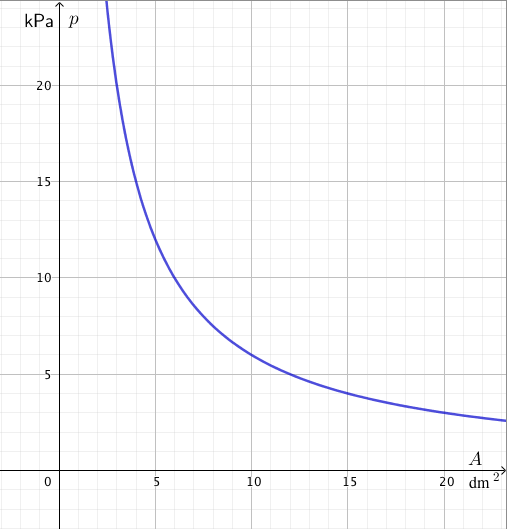
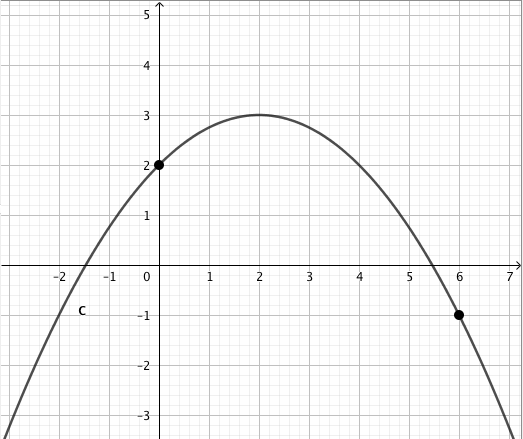
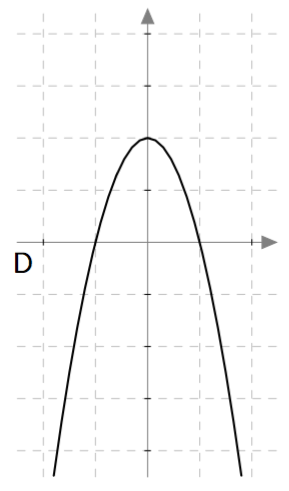
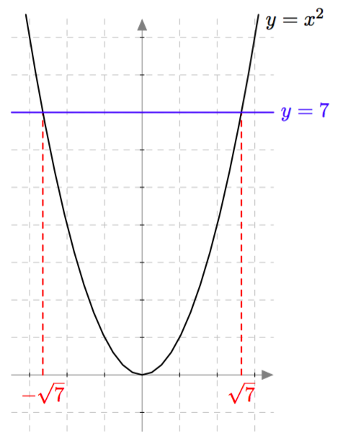
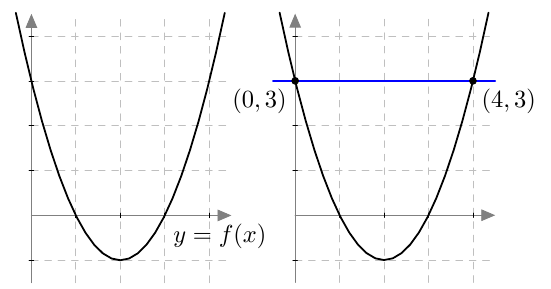
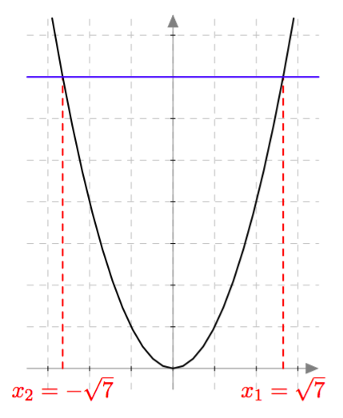
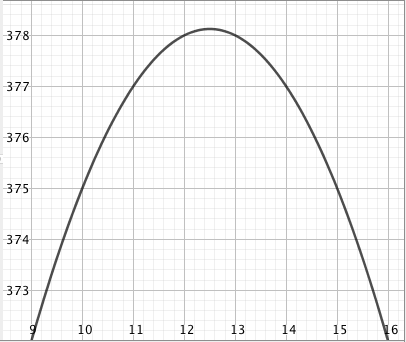
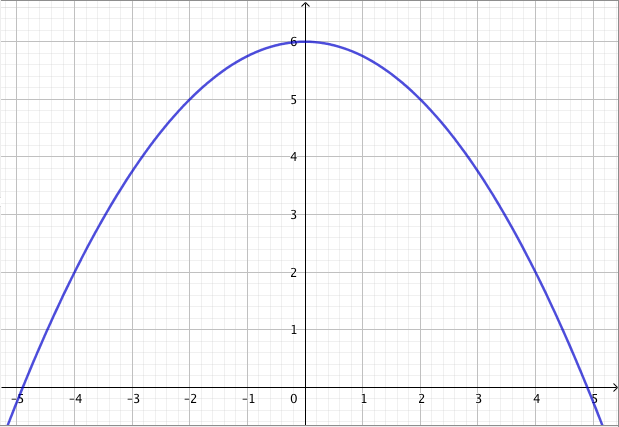
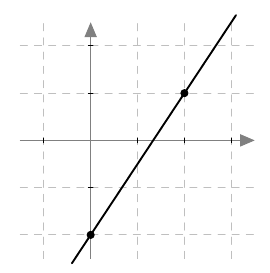
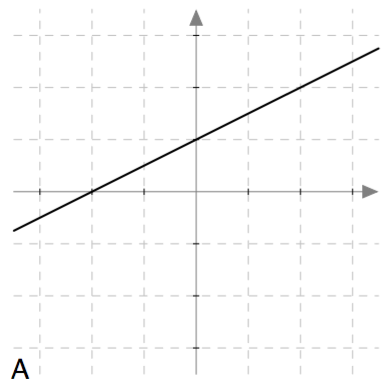
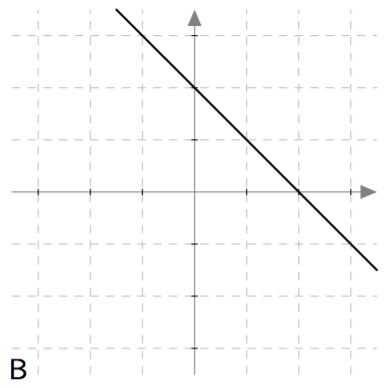
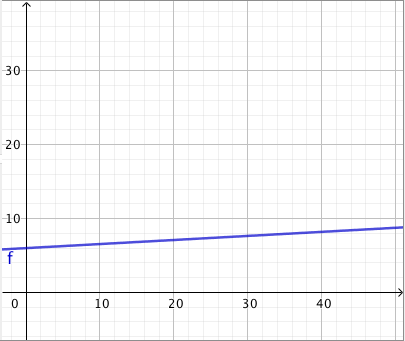
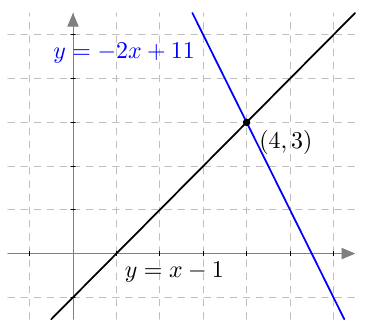
 Päättele kuvaajan avulla vastaukset seuraaviin kysymyksiin:
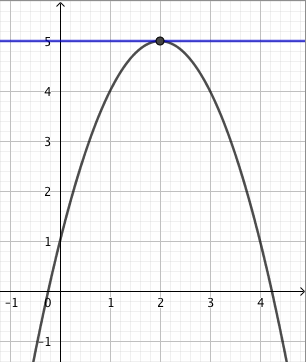
Päättele kuvaajan avulla vastaukset seuraaviin kysymyksiin: