Kisallioppiminen.fi Logo

kisallioppiminen.fi MAA5 - Analyyttinen geometria

$\def\vi{\bar{\imath}} \def\vj{\bar{\jmath}} \def\vv{\bar{v}} \def\vu{\bar{u}} \def\vw{\bar{w}} \def\va{\bar{a}} \def\vb{\bar{b}} \def\vc{\bar{c}} \def\vk{\bar{k}} \def\vn{\bar{n}} \def\pv{\overline} \def\R{\mathbb{R}} \def\Q{\mathbb{Q}} \def\N{\mathbb{N}} \def\Z{\mathbb{Z}} \def\pa{\mathopen]} \def\pe{\mathclose[} \def\lb{\mathop{\mathrm{lb}}} \require{color} \newcommand\T{\Rule{0pt}{1em}{.3em}} \require{mediawiki-texvc} $

Ympyrä

Tämän luvun tavoitteena on, että pystyt hyödyntämään koordinaatistoa erilaisten ympyröihin liittyvien ongelmien ratkaisemisessa. Osaat

  • muodostaa ympyrän yhtälön
  • piirtää ympyrän koordinaatistoon
  • muokata ympyrän yhtälön muotoon, josta ympyrän keskipiste ja säde voidaan päätellä
  • tutkia, onko piste ympyrällä
  • laskea pisteen etäisyyden ympyrästä
  • etsiä kahden ympyrän tai suoran ja ympyrän leikkauspisteet
  • tutkia, onko annettu suora ympyrän tangentti
  • muodostaa ympyrän tangentin yhtälön.

Ympyrän geometriaa olemme opiskelleet jo kurssissa MAA3. Tässä analyyttisen geometrian kurssissa tutkimme ympyröitä koordinaatiston avulla. Aloitetaan palauttamalla mieleen ympyrän määritelmä:

MÄÄRITELMÄ: YMPYRÄ

Tason pisteet, jotka ovat vakioetäisyydellä kiinteästä pisteestä, muodostavat ympyrän eli ympyräviivan. Kiinteä piste on ympyrän keskipiste ja vakioetäisyys sen säde.

Tehtävänä on muodostaa yhtälö ympyrälle, jonka keskipiste on $(4,1)$ ja säde on $5$.

  1. Piirrä ympyrä koordinaatistoon harpin avulla.
  2. Muodosta lauseke ympyrän kehän pisteen $(x,y)$ ja keskipisteen $(4,1)$ väliselle etäisyydelle. Kertaa tarvittaessa Etäisyys-luvun teoreema 5.
  3. Muodosta b-kohdan avulla yhtälö, joka sanoo, että ympyrän kehän pisteen ja keskipisteen etäisyys on $5$.

Seuraavassa teoreemassa johdetaan ympyrän yhtälö käyttämällä samoja ideoita kuin äskeisessä tehtävässä. Lue teoreema ja sen perustelu huolellisesti ja mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.

TEOREEMA

Jos ympyrän keskipiste on $(a,b)$ ja säde $r$, niin ympyrän yhtälö on $$(x-a)^2 + (y-b)^2 = r^2.$$

Perustelu:

  1. Oletetaan aluksi, että $(x,y)$ on ympyrän piste. Tällöin sen etäisyys ympyrän keskipisteestä $(a,b)$ on $r$. Tämä voidaan ilmaista yhtälönä $$ \sqrt{(x-a)^2 + (y-b)^2} = r. $$ Tästä seuraa, että $$ (x-a)^2 + (y-b)^2 = r^2. $$
  2. Oletetaan, että piste $(x,y)$ toteuttaa yhtälön $$ (x-a)^2 + (y-b)^2 = r^2. $$ Yhtälön kumpikin puoli on epänegatiivinen, joten voidaan ottaa neliöjuuri: $$ \sqrt{(x-a)^2 + (y-b)^2} = \sqrt{r^2}. $$ Koska luku $r$ on ympyrän säde, sekin on epänegatiivinen: $r \geq 0$. Tästä seuraa, että $\sqrt{r^2} = r$. Yhtälö voidaan siis kirjoittaa muodossa $$ \sqrt{(x-a)^2 + (y-b)^2} = r. $$ Tästä nähdään, että pisteen $(x,y)$ etäisyys ympyrän keskipisteestä $(a,b)$ on $r$. Siis piste $(x,y)$ on ympyrällä.

Näin on näytetty, että piste $(x,y)$ on ympyrällä, jos ja vain jos se toteuttaa yhtälön $$ \sqrt{(x-a)^2 + (y-b)^2} = r. $$

Ympyrän keskipiste on $(5,-3)$ ja säde on $4$.

  1. Piirrä ympyrä koordinaatistoon harpin avulla.
  2. Muodosta ympyrän yhtälö.
  3. Laske pisteen $P = \left(\frac{3}{2}, -\frac{9}{2}\right)$ etäisyys ympyrän keskipisteestä. Onko piste $P$ ympyrällä?

  1. $(x-5)^2 + (y+3)^2 = 16$
  2. Etäisyys on $\sqrt{\frac{29}{2}}$.

Päättele, mikä on ympyrän keskipiste ja mikä on ympyrän säde, jos ympyrän yhtälö on

  1. $(x-8)^2 + (y+4)^2 = 36$
  2. $(x-14)^2 + y^2 = 8$
  3. $x^2 + y^2 = 20$.

  1. Keskipiste $(8,-4)$, säde $6$.
  2. Keskipiste $(14,0)$, säde $2\sqrt{2}$.
  3. Keskipiste $(0,0)$, säde $2\sqrt{5}$.

Määritä yhtälö ympyrälle, joka

  1. kulkee pisteen $(1,4)$ kautta ja jonka keskipiste on $(-2,3)$
  2. jonka keskipisteenä on $(2,1)$ ja joka kohtaa $y$-akselin täsmälleen yhdessä pisteessä.

Vinkki: alkuun pääset esimerkiksi piirtämällä tilanteesta kuvan.

  1. $(x+2)^2 + (y-3)^2 = 10$
  2. $(x-2)^2 + (y-1)^2 = 4$

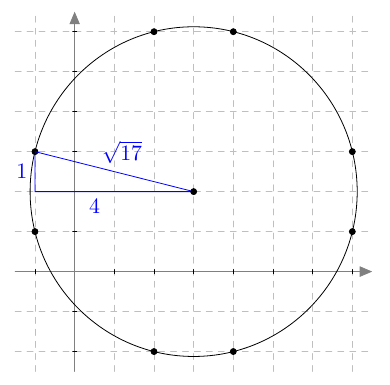
Ympyrän piirtäminen tarkasti harpin avulla onnistuu joissakin tapauksissa silloinkin, kun ympyrän säde on irrationaaliluku. Ideana on soveltaa Pythagoraan lausetta. Esimerkiksi ympyrä, jonka keskipiste on $(3,2)$ ja säde $\sqrt{17}$, voidaan piirtää etsimällä pisteet, joihin päästään keskipisteestä siirtymällä neljä askelta vaakasuunnassa ja yksi askel pystysuunnassa, ja pisteet, joihin päästään keskipisteestä siirtymällä yksi askel vaakasuunnassa ja neljä askelta pystysuunnassa:

Piirrä harpin avulla mahdollisimman tarkasti ympyrä, jonka yhtälö on

  1. $(x+2)^2 + (y-3)^2 = 13$
  2. $(x-5)^2 + (y-4)^2 = 10$

  1. $13 = 3^2 + 2^2$
  2. $10 = 3^2 + 1^2$

Tehtävänä on laskea pisteen $P = (7,1)$ etäisyys ympyrästä $(x-4)^2 + (y+2)^2 = 2$.

  1. Päättele, mikä on ympyrän keskipiste ja mikä on ympyrän säde. Piirrä ympyrä koordinaatistoon. Merkitse näkyviin myös piste $P$.
  2. Laske pisteen $P$ etäisyys ympyrän keskipisteestä.
  3. Päättele pisteen $P$ etäisyys ympyrästä.

  2. $3\sqrt{2}$
  3. $2\sqrt{2}$

Ympyrän yhtälö voidaan aina muokata muotoon $$x^2 + y^2 + ax + by + c = 0.$$ Esimerkiksi ympyrän, jonka keskipiste on $(7,-9)$ ja säde on $4$, yhtälö on $$(x-7)^2 + (y+9)^2 = 16.$$ Kun yhtälön vasemmalla puolella tehdään potenssiin korotukset, yhtälö saa muodon $$x^2 - 14x + 49 + y^2 + 18y + 81 = 16$$ eli $$x^2 + y^2 - 14x + 18y + 114 = 0.$$ Huomaa, että potenssiin korotukset voi tehdä joko kertomalla sulut auki tai käyttämällä MAA2-kurssilta tuttuja summan neliön ja erotuksen neliön muistikaavoja:

TEOREEMA

  1. $\quad a^2 + 2ab + b^2 = (a+b)^2$
  2. $\quad a^2 - 2ab + b^2 = (a-b)^2$

Tutkitaan seuraavaksi, esittääkö muotoa $$x^2 + y^2 + ax + by + c = 0$$ oleva yhtälö aina ympyrää. Tarkastellaan esimerkiksi yhtälöä $$x^2 + y^2 - 4x + 2y + c = 0.$$ Tunnistetaan ja ryhmitellään ensin yhteenlaskettavat summan neliön ja erotuksen neliön muistikaavojen mukaisesti: \begin{align*} \textcolor{blue}{x^2} + \textcolor{red}{y^2} \textcolor{blue}{- 4x} \textcolor{red}{+ 2y} + c &= 0 \\ \textcolor{blue}{x^2- 4x} + \textcolor{red}{y^2 + 2y} + c &= 0 \end{align*} Lisätään sen jälkeen yhtälön molemmille puolille termejä niin, että vasemmalle saadaan muistikaavojen mukaiset lausekkeet: \begin{align*} \textcolor{blue}{x^2- 4x + 2^2} + \textcolor{red}{y^2 + 2y + 1^2} + c &= \textcolor{blue}{2^2}\textcolor{red}{+1^2} \end{align*} Nyt muistikaavojen avulla vasemmalle puolelle saadaan neliöt: \begin{align*} \textcolor{blue}{(x-2)^2} + \textcolor{red}{(y+1)^2} + c &= 5. \end{align*} Lopuksi yhtälö voidaan kirjoittaa muodossa, josta ympyrän keskipiste ja säde on helppo tunnistaa: \begin{align*} (x-2)^2 + (y+1)^2 &= 5-c. \end{align*} Havaitaan, että tämän yhtälön vasen puoli on aina epänegatiivinen, koska se on kahden neliölausekkeen summa. Se, mitä käyrää yhtälö esittää, riippuu nyt yhtälön oikeasta puolesta.

  • Jos $5-c > 0$, kysymyksessä on ympyrä, jonka keskipiste on $(2,-1)$ ja säde $\sqrt{5-c}$.
  • Jos $5-c = 0$, yhtälön toteuttaa ainoastaan piste $(2,-1)$.
  • Jos $5-c < 0$, mikään tason piste ei toteuta yhtälöä.

Vastaavalla tavalla voidaan osoittaa yleisesti, että yhtälön $$x^2 + y^2 + ax + by + c = 0$$ ratkaisujoukko on joko ympyrä tai yksittäinen piste, tai ratkaisuja ei ole lainkaan.

Määritä ympyrän keskipiste ja säde, jos ympyrän yhtälö on

  1. $x^2 + y^2 + 2x - 3 = 0$
  2. $x^2+y^2 + 10x - 6y - 66 = 0$.

  1. Keskipiste $(-1,0)$ ja säde $r = 2$.
  2. Keskipiste $(-5,3)$ ja säde $r = 10$.

Tutki, onko yhtälön toteuttavia pisteitä olemassa. Jos niitä on olemassa, onko kysymyksessä ympyrä vai yksittäinen piste? Ympyrän tapauksessa selvitä sen keskipiste ja säde.

  1. $x^2 + y^2 - 16x + 2y + 65 = 0$
  2. $x^2+y^2 + 8x - 24y + 165 = 0$
  3. $x^2+y^2 + 22y - 104 = 0$.

  1. Yksittäinen piste $(8,-1)$.
  2. Mikään tason piste ei toteuta yhtälöä.
  3. Ympyrä, jonka keskipiste on $(0,-11)$ ja säde $15$.

Tässä kappaleessa tutkitaan kahden ympyrän sekä suoran ja ympyrän leikkauspisteitä. Aloitetaan tarkastelemalla kahden ympyrän leikkauspisteitä.

Tehtävänä on ratkaista alla oleva yhtälöpari graafisesti eli piirroksen avulla. $$ \left\{\begin{aligned} (x+3)^2 + (y-1)^2 &= 20 \\ (x-2)^2 + (y-6)^2 &= 10. \end{aligned}\right. $$

  1. Piirrä koordinaatistoon ne pisteet, jotka toteuttavat yhtälön $(x+3)^2 + (y-1)^2 = 20$. Millaisen kuvion ne muodostavat?
  2. Piirrä samaan koordinaatistoon ne pisteet, jotka toteuttavat yhtälön $(x-2)^2 + (y-6)^2 = 10$. Millaisen kuvion ne muodostavat?
  3. Kuinka moni piste toteuttaa yhtälöparin molemmat yhtälöt? Mitkä ovat näiden pisteiden koordinaatit?
  4. Mitkä ovat yhtälöparin ratkaisut?

  4. Yhtälöpari toteutuu, jos ja vain jos $$ \left\{\begin{aligned} x &= -1 \\ y &= 5 \end{aligned}\right. $$ tai $$ \left\{\begin{aligned} x &= 1 \\ y &= 3. \end{aligned}\right. $$

Kahden ympyrän leikkauspisteet löydetään ratkaisemalla ympyröiden yhtälöistä muodostuva yhtälöpari. Tällaiseen yhtälöpariin kannattaa soveltaa luvussa Suora opiskeltua yhteenlaskumenetelmää. Seuraava esimerkki havainnollistaa asiaa.

Tarkastellaan edellisen tehtävän yhtälöparia $$ \left\{\begin{aligned} (x+3)^2 + (y-1)^2 &= 20 \\ (x-2)^2 + (y-6)^2 &= 10 \end{aligned}\right. $$ Tehdään yhtälöiden vasemmalla puolella toiseen potenssiin korotukset, jolloin yhtälöpari saadaan sievennysten jälkeen muotoon $$ \left\{\begin{aligned} x^2 + y^2 + 6x - 2y &= 10 \\ x^2 + y^2 - 4x - 12y &= -30. \end{aligned}\right. $$ Ratkaistaan tämä yhtälöpari soveltamalla yhteenlaskumenetelmää. Kerrotaan toinen yhtälö luvulla $-1$: $$ \left\{\begin{aligned} \textcolor{red}{x^2 + y^2} + 6x - 2y &= 10 \\ \textcolor{red}{x^2 + y^2} - 4x - 12y &= -30 \mid \, \textcolor{red}{\cdot \, (-1)} \end{aligned}\right. $$ Yhtälöpari saa näin muodon $$ \left\{\begin{aligned} \textcolor{red}{x^2 + y^2} + 6x - 2y &= 10 \\ \textcolor{red}{-x^2 - y^2} \textcolor{blue}{+ 4x + 12y} &= \textcolor{blue}{30}. \end{aligned}\right. $$ Lasketaan yhtälöt yhteen, jolloin saadaan yksi yhtälö. Nyt tuloksena on yhtälö $$10x + 10y = 40.$$ Ratkaistaan tästä toinen tuntematon, esimerkiksi $$y = 4-x.$$ Ympyröiden leikkauspisteet sijaitsevat tätä yhtälöä vastaavalla suoralla:

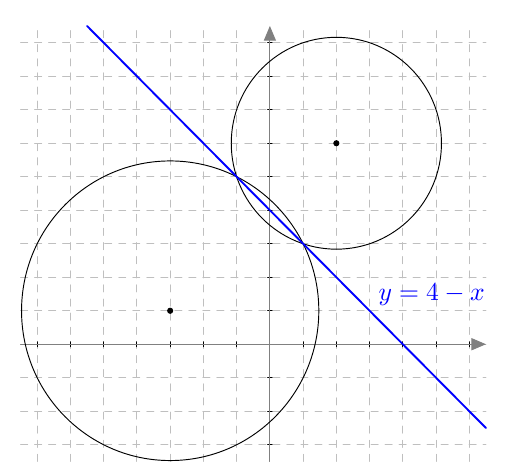
Sijoitetaan saatu lauseke jompaan kumpaan alkuperäisistä yhtälöistä, esimerkiksi ensimmäiseen ja sievennetään: \begin{align*} x^2 + (4-x)^2 + 6x - 2(4-x) &= 10 \\ &\ \vdots \\ 2x^2 &= 2 \ \mid \, : 2\\ x^2 &= 1 \end{align*} Tämä yhtälö toteutuu, jos ja vain jos $x = 1$ tai $x = -1$. Leikkauspisteiden $y$-koordinaatit voidaan ratkaista esimerkiksi kohdassa 2 johdetusta yhtälöstä $y = 4-x$:

  • Jos $x = 1$, niin $y = 4-1 = 3$.
  • Jos $x = -1$, niin $y = 4-(-1) = 5$.
Leikkauspisteet ovat siis $(1,3)$ ja $(-1,5)$.

Määritä ympyröiden $(x-9)^2 + (y-1)^2 = 40$ ja $(x+3)^2 + (y+5)^2 = 100$ leikkauspisteet ratkaisemalla yhtälöpari samaan tapaan kuin edellä tehtiin. Voit tarkistaa ratkaisun järkevyyden hahmottelemalla ympyrät koordinaatistoon.

Leikkauspisteet ovat $(3,3)$ ja $(7,-5)$.

Siirrytään seuraavaksi tutkimaan suoran ja ympyrän leikkauspisteitä.

Tehtävänä on ratkaista alla oleva yhtälöpari graafisesti eli piirroksen avulla. $$ \left\{\begin{aligned} x + y - 5 &= 0 \\ (x-3)^2 + (y-1)^2 &= 13. \end{aligned}\right. $$

  1. Piirrä koordinaatistoon ne pisteet, jotka toteuttavat yhtälön $x + y - 5 = 0$. Millaisen kuvion ne muodostavat?
  2. Piirrä samaan koordinaatistoon ne pisteet, jotka toteuttavat yhtälön $(x-3)^2 + (y-1)^2 = 13$. Millaisen kuvion nämä pisteet muodostavat?
  3. Kuinka moni piste toteuttaa yhtälöparin molemmat yhtälöt? Mitkä ovat näiden pisteiden koordinaatit?
  4. Mitkä ovat yhtälöparin ratkaisut?

  4. Yhtälöpari toteutuu, jos ja vain jos $$ \left\{\begin{aligned} x &= 1 \\ y &= 4 \end{aligned}\right. $$ tai $$ \left\{\begin{aligned} x &= 6 \\ y &= -1. \end{aligned}\right. $$

Suoran ja ympyrän yhtälöistä muodostuva yhtälöpari on kätevintä ratkaista sijoitusmenetelmällä, jota käytettiin jo kurssissa MAA4. Havainnollistetaan menetelmää seuraavan esimerkin avulla.

Etsitään suoran $x + 2y - 11 = 0$ ja ympyrän $x^2+y^2 + 4x - 8y + 10 = 0$ leikkauspisteet ratkaisemalla yhtälöpari $$ \left\{\begin{aligned} x + 2y - 11 &= 0 \\ x^2+y^2 + 4x - 8y + 10 &= 0. \end{aligned}\right. $$ Ratkaistaan suoran yhtälöstä jompi kumpi tuntemattomista. Esimerkiksi $$x = 11-2y.$$ Sijoitetaan saatu lauseke ympyrän yhtälöön ja sievennetään: \begin{align*} ({\scriptstyle 11-2y})^2 + y^2 + 4({\scriptstyle 11-2y}) - 8y + 10 &= 0 \\ &\vdots \\ 5y^2 - 60y + 175 &= 0 \ \mid \, : 5\\ y^2 - 12y + 35 &= 0 \end{align*} Saatu toisen asteen yhtälö voidaan ratkaista toisen asteen yhtälön ratkaisukaavan avulla (MAA2, teoreema 5). $$ y = \frac{12\pm \sqrt{12^2 - 4\cdot 35}}{2\cdot 1} = 6 \pm 1. $$ Siis $y = 7$ tai $y = 5$. Toinen tuntematon saadaan nyt selville sijoittamalla äsken saatu ratkaisu suoran yhtälöön: $$x = 11 - 2\cdot 7 = -3$$ tai $$x = 11 - 2\cdot 5 = 1.$$ Etsityt leikkauspisteet ovat siis $(-3,7)$ ja $(1,5)$.

Tarkastellaan suoraa $3x + y - 5 = 0$ ja ympyrää $x^2 + y^2 - 10x + 2y + 1 = 0$.

  1. Määritä suoran ja ympyrän leikkauspisteet.
  2. Muokkaa ympyrän yhtälö neliöksi täydentämällä muotoon, josta voit päätellä ympyrän keskipisteen ja säteen. Tarkista a-kohdan tuloksen järkevyys piirtämällä ympyrä ja suora koordinaatistoon.

  1. Leikkauspisteet ovat $(1,2)$ ja $\left(\frac{18}{5}, -\frac{29}{5}\right)$.
  2. Keskipiste $(5,-1)$ ja säde $r = 5$.

Edellisessä luvussa tutkittiin suoran ja ympyrän leikkauspisteitä. Jos suoralla ja ympyrällä on tasan yksi yhteinen piste, sanotaan suoraa ympyrän tangentiksi.

MÄÄRITELMÄ: YMPYRÄN TANGENTTI

Suora, joka kohtaa ympyrän vain yhdessä pisteessä, on ympyrän tangentti.

Onko suora $3x - y - 5 = 0$ ympyrän $x^2 + y^2 + 4x + 2y - 5 = 0$ tangentti? Ratkaise tehtävä selvittämällä suoran ja ympyrän leikkauspisteet. Tarkista vastauksesi järkevyys piirtämällä tilanteesta kuva.

Kyllä, suora on ympyrän tangentti, sillä niillä on vain yksi yhteinen piste.

Ympyrän tangenttiin tutustuttiin jo kurssilla MAA3. Siellä osoitettiin muun muassa, että ympyrän tangetti on aina kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan (teoreema 15). Tämän tiedon avulla voidaan määrittää ympyrän tietyn pisteen kautta kulkevan tangentin yhtälö.

Tehtävänä on määrittää yhtälö ympyrän $(x-3)^2 + (y+1)^2 = 20$ sille tangentille, joka kulkee pisteen $(1,-5)$ kautta.

  1. Tunnista ympyrän yhtälöstä keskipiste ja säde. Piirrä ympyrä koordinaatistoon.
  2. Laske pisteen $(1,-5)$ etäisyys ympyrän keskipisteestä. Onko piste $(1,-5)$ ympyrällä?
  3. Määritä kulmakerroin suoralle, joka kulkee ympyrän keskipisteen ja pisteen $(1,-5)$ kautta. Mikä on sitä vastaan kohtisuorassa olevan suoran kulmakerroin?
    Kertaa tarvittaessa luvun Suora teoreema 11.
  4. Muodosta yhtälö ympyrän $(x-3)^2 + (y+1)^2 = 20$ tangentille, joka kulkee pisteen $(1,-5)$ kautta.

  2. Kyllä, piste on ympyrällä.
  4. $y = -\frac{1}{2}x - \frac{9}{2}$

Tutkitaan seuraavaksi, miten löydetään yhtälö tietyn pisteen kautta kulkevalle tangentille tapauksessa, jossa piste ei ole ympyrällä. Tässä tilanteessa oleellista on, että ympyrän keskipisteen etäisyys tangenttisuorasta on yhtä suuri kuin ympyrän säde. Näin voidaan hyödyntää edellisen luvun Pisteen etäisyys suorasta -teoreemaa.

Tehtävänä on määrittää yhtälö ympyrän $(x-3)^2 + (y+1)^2 = 20$ tangentille, joka kulkee pisteen $(5,5)$ kautta.

  1. Tunnista ympyrän yhtälöstä keskipiste ja säde. Piirrä ympyrä koordinaatistoon. Merkitse näkyviin myös piste $(5,5)$ ja hahmottele ympyrälle sen kautta kulkeva tangentti. Kuinka monta tällaista tangenttia on olemassa?
  2. Merkitään etsityn tangentin kulmakerrointa kirjaimella $k$. Muodosta yhtälö suoralle, joka kulkee pisteen $(5,5)$ kautta ja jonka kulmakerroin on $k$.
    Kertaa tarvittaessa luvun Suora teoreema 9.
  3. Muokkaa tangenttisuoran yhtälö normaalimuotoon.
  4. Muodosta teoreeman 13 avulla yhtälö, joka ilmaisee, että ympyrän keskipisteen etäisyys tangettisuorasta on yhtä suuri kuin ympyrän säde. Yhtälöön pitäisi jäädä vain yksi tuntematon, kulmakerroin $k$.
  5. Ratkaise saamasi yhtälö laskimen tai tietokoneen avulla. Mikä on etsitty tangentin yhtälö? Tarkista vastauksesi järkevyys vertaamalla sitä a-kohdassa piirtämääsi kuvaan.

  2. $y-5 = k(x-5)$
  4. $\dfrac{\left|6-2k\right|}{\sqrt{k^2+1}} = \sqrt{20}$
  5. Tangentteja on kaksi: $y = -2x + 15$ ja $y = -\frac{1}{2}x + \frac{5}{2}$.

Edellisessä tehtävässä päädyttiin ratkaisemaan yhtälö $$\frac{\left|6-2k\right|}{\sqrt{k^2+1}} = \sqrt{20}.$$ Tällaiset yhtälöt voidaan ratkaista toiseen potenssiin korottamalla seuraavasti:

Jos yhtälön vasen ja oikea puoli ovat yhtä suuret, myös niiden toiset potenssit ovat yhtä suuret: $$\left(\frac{\left|6-2k\right|}{\sqrt{k^2+1}}\right)^2 = \left(\sqrt{20}\right)^2.$$ Potenssin laskusääntöjen (MAY1) mukaan osamäärän potenssi on sama kuin potenssien osamäärä, joten yhtälö voidaan kirjoittaa muodossa $$\frac{\left(6-2k\right)^2}{\left(\sqrt{k^2+1}\right)^2} = \left(\sqrt{20}\right)^2.$$ Huomaa, että itseisarvomerkkejä ei enää tarvita osoittajassa, koska toiseen potenssiin korotus tekee kaikista luvuista epänegatiivisia.

Neliöjuuren määritelmän (MAA2) mukaan $\left(\sqrt{a}\right)^2 = a$ eli neliöjuuri on luku, jonka toinen potenssi on yhtä suuri kuin juurrettava. Tämän nojalla yhtälö voidaan kirjoittaa muodossa $$\frac{\left(6-2k\right)^2}{k^2+1} = 20.$$ Kerrotaan kumpikin puoli nimittäjällä $k^2+1$, jolloin se supistuu vasemmalta puolelta pois: $$(6-2k)^2 = 20(k^2 + 1).$$ Nyt vasemmalla voidaan tehdä toiseen potenssiin korotukset ja muokata yhtälöä: \begin{align*} 36-24k + 4k^2 &= 20k^2 + 20 \\ -16k^2-24k + 16 &= 0 \ \mid \, : (-8)\\ 2k^2 + 3k - 2 &= 0 \end{align*} Tämä yhtälö toteutuu, jos ja vain jos \begin{align*} k &= \frac{-3 \pm \sqrt{3^2 - 4\cdot 2\cdot (-2)}}{2\cdot 2} \\ &= \frac{-3 \pm 5}{4}. \end{align*} Ratkaisuiksi saadaan näin $k_1 = \frac{1}{2}$ ja $k_2 = -2$. Ovatko nämä myös alkuperäisen yhtälön $$\frac{\left|6-2k\right|}{\sqrt{k^2+1}} = \sqrt{20}$$ ratkaisuja?

Koska yhtälön ratkaiseminen aloitettiin toiseen potenssiin korottamisella, on varminta ja yksinkertaisinta tarkistaa saadut ratkaisut sijoittamalla ne alkuperäiseen yhtälöön. Joissain tilanteissa toiseen potenssiin korotus tuottaa "ratkaisuja", jotka eivät toteuta alkuperäistä yhtälöä. Tätä ilmiötä tarkastellaan enemmän seuraavan luvun kappaleessa Itseisarvo koordinaatistossa.

Tällä kertaa kumpikin ratkaisuehdokas on alkuperäisen yhtälön ratkaisu, sillä \begin{align*} \frac{\left|6-2 \cdot \frac{1}{2}\right|}{\sqrt{\left(\frac{1}{2}\right)^2+1}} &= \frac{5}{\sqrt{\frac{5}{4}}} = \frac{5}{\frac{\sqrt{5}}{\sqrt{4}}} \\[1mm] &= 5 \cdot \frac{\sqrt{4}}{\sqrt{5}} \\[1mm] &= \sqrt{5}\cdot \sqrt{4} = \sqrt{20} \end{align*} ja \begin{align*} \frac{\left|6-2\cdot (-2)\right|}{\sqrt{(-2)^2+1}} &= \frac{10}{\sqrt{5}} = \frac{\sqrt{100}}{\sqrt{5}} \\[1mm] &= \sqrt{\frac{100}{5}} \\[1mm] &= \sqrt{20}. \end{align*} Tässä käytettiin MAA2-kurssissa opiskeltuja neliöjuuren laskusääntöjä.

Pisteen etäisyys suorasta -teoreemaan perustuvalla menetelmällä voidaan määrittää myös ympyrän tietyn suuntaisen tangentin yhtälö. Tätä harjoitellaan seuraavassa tehtävässä.

Tehtävänä on määrittää yhtälö ympyrän $(x-3)^2 + (y+1)^2 = 20$ tangentille, joka on yhdensuuntainen suoran $y = 2x$ kanssa.

  1. Tunnista ympyrän yhtälöstä keskipiste ja säde. Piirrä ympyrä koordinaatistoon. Hahmottele sille tangentti, joka on yhdensuuntainen suoran $y = 2x$ kanssa. Kuinka monta tällaista tangenttia on olemassa?
  2. Muodosta yhtälö tangettisuoralle, joka on yhdensuuntainen suoran $y = 2x$ kanssa ja joka leikkaa $y$-akselin korkeudella $h$.
    Kertaa tarvittaessa luvun Suora teoreema 8.
  3. Muokkaa tangenttisuoran yhtälö normaalimuotoon.
  4. Muodosta teoreeman 13 avulla yhtälö, joka ilmaisee, että ympyrän keskipisteen etäisyys tangettisuorasta on yhtä suuri kuin ympyrän säde. Yhtälöön pitäisi jäädä vain yksi tuntematon, korkeus $h$.
  5. Ratkaise saamasi yhtälö kynän ja paperin avulla samaan tapaan kuin edellä tehtiin. Mikä on etsitty tangentin yhtälö? Tarkista vastauksesi järkevyys vertaamalla sitä a-kohdassa piirtämääsi kuvaan.

  2. $y = 2x + h$
  4. $\dfrac{\left|7+h\right|}{\sqrt{5}} = \sqrt{20}$
  5. Tangentteja on kaksi: $y = 2x + 3$ ja $y = 2x - 17$.

Ympyrän yhtälö

Tehtävänä on määrittää yhtälö ympyrälle, jonka yksi halkaisija on pisteiden $(-1,1)$ ja $(5,-2)$ välinen jana.

  1. Laske tai päättele halkaisijan keskipisteen koordinaatit. Voit tarkistaa vastauksesi piirtämällä tilanteesta kuvan.
  2. Määritä ympyrän säde. Keksitkö erilaisia tapoja?
  3. Muodosta ympyrän yhtälö.

  3. $\left(x - 2\right)^2 + \left(y + \frac{1}{2}\right)^2 = \frac{45}{4}$

Ympyrän yhtälö

Määritä ympyrän keskipiste ja säde, jos ympyrän yhtälö on

  1. $x^2 + y^2 + 2x - 3 = 0$
  2. $x^2 + y^2 - 2x - 4y - 4 = 0$.

Vinkki: sovella summan ja erotuksen neliöiden kaavoja (teoreema 15).

  1. Keskipiste on $(-1,0)$ ja säde $2$.
  2. Keskipiste on $(1,2)$ ja säde $3$.

Pisteen etäisyys ympyrästä

Tehtävänä on laskea origon etäisyys ympyrästä $x^2 + y^2 + 4x - 3y - 6 = 0$.

  1. Selvitä ympyrän keskipiste ja säde.
  2. Laske kysytty etäisyys. Kuvan hahmottelusta voi olla apua.

  1. Keskipiste on $\left(-2,\frac{3}{2}\right)$ ja säde $\frac{7}{2}$.
  2. Etäisyys on $1$.

Ympyröiden välinen etäisyys

Piirrä koordinaatistoon ympyrät $(x+3)^2 + (y-2)^2 = 16$ ja $(x+2)^2 + (y-1)^2 = 1$ ja määritä niiden välinen etäisyys.

Etäisyys on $3 - \sqrt{2}$. (Hyödynnä ympyröiden säteitä ja niiden keskipisteiden välistä etäisyyttä.)

Ympyrän yhtälö

Tehtävänä on muodostaa yhtälö ympyrälle, joka kulkee pisteiden $(2,-1)$ ja $(-1,3)$ kautta ja jonka keskipiste on suoralla $x - 2y = 0$.

  1. Jos ympyrän keskipisteen $y$-koordinaatti on $t$, niin mikä on sen $x$-koordinaatti?
  2. Mitä tiedetään pisteiden $(2,-1)$ ja $(-1,3)$ etäisyyksistä ympyrän keskipisteeseen? Muodosta sopiva yhtälö.
  3. Mikä on ympyrän keskipiste?
  4. Mikä on ympyrän yhtälö?

  3. $\left(-\frac{5}{2}, -\frac{5}{4}\right)$
  4. $\left(x+\frac{5}{2}\right)^2 + \left(y+\frac{5}{4}\right)^2 = \frac{325}{16}$

Ympyrän yhtälö

Tutkitaan yhtälöä $x^2 + y^2 + ax + a = 0$.

  1. Muokkaa yhtälö muotoon, josta voit tunnistaa ympyrän keskipisteen ja säteen.
    Vinkki: Termin $ax$ voi kirjoittaa myös muodossa $2\cdot \frac{1}{2}ax$. Myös teoreemasta 15 on apua.
  2. Millä vakion $a$ arvoilla yhtälö esittää ympyrää?
    Vinkki: mieti, millainen ympyrän säteen pitää olla.
  3. Millä vakion $a$ arvoilla yhtälö esittää jotain muuta kuin ympyrää? Mitä?

  1. $\left(x+\frac{1}{2}a\right)^2 + \left(y-0\right)^2 = \frac{1}{4}a^2 - a$
  2. Jos $a < 0$ tai $a > 4$.
  3. Jos $a = 0$ yhtälö esittää pistettä $(0,0)$. Jos $a = 4$, yhtälö esittää pistettä $(-2,0)$. (Jos $0 < a < 4$, mikään tason piste ei toteuta yhtälöä).

Ympyrän yhtälö

Tehtävänä on näyttää, että suora $x + ay - 3 = 0$ kulkee ympyrän $x^2 + y^2 - 6x + 5 = 0$ keskipisteen kautta vakion $a$ arvosta riippumatta.

  1. Muokkaa ympyrän yhtälö muotoon, josta voit tunnistaa ympyrän keskipisteen ja säteen.
  2. Tutki, toteuttavatko ympyrän keskipisteen koordinaatit suoran yhtälön.
  3. Kirjoita omin sanoin perustelu sille, että suora $x + ay - 3 = 0$ kulkee ympyrän $x^2 + y^2 - 6x + 5 = 0$ keskipisteen kautta vakion $a$ arvosta riippumatta.

  1. $\left(x-3\right)^2 + \left(y-0\right)^2 = 2^2$
  2. $3 + a\cdot 0 - 3 = 3 + 0 - 3 = 0$, joten piste $(3,0)$ toteuttaa yhtälön $x + ay - 3 = 0$.

Ympyrän leikkauspisteitä

Määritä ympyröiden $x^2 + y^2-2x-4y-3 = 0$ ja $x^2 + y^2 + 4x + 2y - 21 = 0$ leikkauspisteet.

$(3,0)\ $ ja $\ (-1,4)$

Ympyrän leikkauspisteitä

Tehtävänä on laskea sen jänteen pituus, jonka ympyrä $x^2 + y^2 = 10$ erottaa suorasta $x + y - 2 = 0$.

  1. Piirrä ympyrä ja suora koordinaatistoon mahdollisimman tarkasti.
  2. Mikä on jänteen pituus?

  1. Vinkki: Ympyrän säde on tietyn suorakulmaisen kolmion hypotenuusa; vrt. esimerkki ennen tehtävää 3.5.
  2. Jänteen pituus on $4\sqrt{2}$. (Jänteen päätepisteiden koordinaatit ovat $(-1,3)\ $ ja $\ (3,-1)$.)

Ympyrän leikkauspisteitä

Mitkä suoran $y = 5-3x$ pisteet ovat etäisyydellä $5$ pisteestä $(5,-1)$?

Pisteet $(1,2)\ $ ja $\ \left(\frac{18}{5}, - \frac{29}{5}\right)$.

Ympyrän tangentti

Määritä ympyrän $x^2 + y^2 = 25$ pisteeseen $(-3,4)$ piirretyn tangentin yhtälö.

$y = \frac{3}{4}x + \frac{25}{4}$

Ympyrän tangentti

Tehtävänä on muodostaa yhtälö ympyrän $(x-5)^2 + (y-5)^2 = 5$ tangentille, joka kulkee origon kautta.

  1. Piirrä ympyrä koordinaatistoon mahdollisimman tarkasti. Miten voit laskemalla varmistaa, että piste $(0,0)$ ei ole ympyrällä?
  2. Hahmottele kuvaan ympyrän tangetteja, jotka kulkevat origon kautta. Kuinka monta niitä on?
  3. Muodosta kysytty tangetin yhtälö.

  1. Vinkki: Ympyrän säde on tietyn suorakulmaisen kolmion hypotenuusa; vrt. esimerkki ennen tehtävää 3.5.
  2. Tangentteja on kaksi.
  3. Tangetteja on kaksi: $y = \frac{1}{2}x$ ja $y = 2x$. (Vinkki: Origon kautta kulkeva suora on muotoa $y = kx$. Ympyrän keskipisteen etäisyys tangenttisuorasta on yhtä suuri kuin ympyrän säde.)

Ympyrän tangentti

Muodosta yhtälö ympyrän $x^2 + y^2 = 1$ tangentille, joka kulkee pisteen $(2,-1)$ kautta.

Tangentteja on kaksi: $y = -1$ ja $4x + 3y - 5 = 0$.

Ympyrän tangentti

Muodosta yhtälö ympyrän $x^2 + y^2 -2x - y - 3 = 0$ tangentille, joka kulkee pisteen $(3,1)$ kautta.

$y = -4x + 13$.

Ympyrän tangentti

Tehtävänä on muodostaa yhtälö ympyrän $x^2 + y^2 = 8$ tangentille, joka on suoran $y = 3x$ suuntainen.

  1. Piirrä ympyrä koordinaatistoon mahdollisimman tarkasti.
    Vinkki: Ympyrän säde on tietyn suorakulmaisen kolmion hypotenuusa.
  2. Hahmottele kuvaan ympyrän tangetteja, jotka ovat suoran $y = 3x$ suuntaisia. Kuinka monta niitä on?
  3. Mitä muotoa tangettisuoran yhtälö on? Mikä on ympyrän keskipisteen etäisyys tästä suorasta?
  4. Muodosta kysytty tangetin yhtälö.

  2. Tangentteja on kaksi.
  3. $y = 3x + h$, keskipisteen etäisyys tangetista on yhtä suuri kuin ympyrän säde.
  4. Tangetteja on kaksi: $y = 3x + 4\sqrt{5}$ ja $y = 3x-4\sqrt{5}$.

Määritä yhtälö sille origokeskiselle ympyrälle, joka sivuaa suoraa $7x + 24y - 75 = 0$.

$x^2 + y^2 = 3$.

Ympyrän $x^2 + y^2 = 16$ jänteen keskipiste on $(2,1)$. Määritä jänteen pituus.
[Pitkä S2015/5]

Jänteen pituus on $2\sqrt{11}$.

Ympyrä sivuaa suoraa $3x-4y = 0$ pisteessä $(8,6)$. Lisäksi se sivuaa positiivista $x$-akselia. Määritä ympyrän keskipiste ja säde.
[Pitkä K2014/5]

Keskipiste on $\left(10, \frac{10}{3}\right)$ ja säde $\frac{10}{3}$.

Laske suoran $y = 2x$ ja ympyrän $x^2 + y^2 = 1$ leikkauspisteet.
[Pitkä S2011/2b]

Leikkauspisteet ovat $\left(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right)$ ja $\left(-\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}}\right)$.

Määritä ympyrän $x^2 + y^2 + 4x - 2y + 1 = 0$ niiden tangenttien yhtälöt, jotka kulkevat pisteen $(1,3)$ kautta.
[Pitkä S2007/5]

Tangenttien yhtälöt ovat $y = 3$ ja $12x - 5y + 3 = 0$.

Etsi yhtälö ympyrälle, jonka keskipiste on suoralla $y = \frac{1}{2}x$ ja joka sivuaa $x$-akselia ja suoraa $4x + 3y - 24 = 0$. Määritä kaikki tehtävän ratkaisut.
[Pitkä K2006/7]

Sopivia ympyröitä on kaksi: $(x-8)^2 + (y-4)^2 = 16$ ja $(x-3)^2 + \left(y-\frac{3}{2}\right)^2 = \frac{9}{4}$.

Oletetaan, että $a \neq 0$. Suora $x-y-a = 0$ jakaa ympyrän $x^2 + y^2 = a^2$ rajoittaman alueen kahteen osaan. Määritä pienemmän alueen pinta-alan suhde suuremman alueen pinta-alaan. Ilmoita tarkka arvo ja kolmidesimaalinen likiarvo. Piirrä kuvio, kun (a) $a > 0$, (b) $a < 0$.
[Pitkä S2005/6]

Suhde on $\frac{\pi - 2}{3\pi + 2} \approx 0{,}100$.

Osa tien kaarteesta on ympyrän kaari, joka kartalla kulkee $xy$-koordinaatiston pisteiden $\ (28,98)$, $\ (70,112)\ $ ja $\ (126,84)\ $ kautta. Kuinka suuri on tämän ympyrän säde, kun yksikkö kartalla vastaa 25 metriä luonnossa.
[Pitkä S2001/10]

Säde on 1750 metriä.

Piste $P$ on ympyrän $x^2 + y^2 + 2x - y - 5 = 0$ kehällä ja piste $Q$ on ympyrän $x^2 + y^2 - 6x + y + 9 = 0$ kehällä. Laske janan $PQ$ pienin mahdollinen pituus eli ympyröiden välinen etäisyys.

Etäisyys on $\sqrt{17} - 3$.
Vinkki: aloita selvittämällä ympyröiden keskipisteet ja säteet.

Oletetaan, että $a \neq -2$. Osoita, että ympyröillä $x^2 + y^2 - 2ax + 2ay = 8a + 8$ on yhteinen tangentti riippumatta vakion $a$ arvosta. Mikä on tämän tangentin yhtälö?

Tangetin yhtälö on $y = x + 4$.

Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.