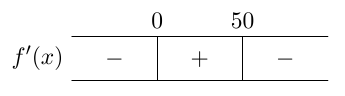
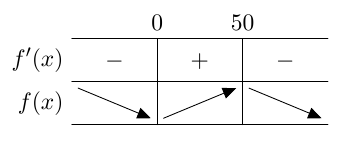
MAA6 - Derivaatta
Kurssin tavoitteet ja keskeiset sisällöt
Kurssin tavoitteena on, että
- osaat määrittää rationaalifunktion nollakohdat ja ratkaista yksinkertaisia rationaaliepäyhtälöitä
- omaksut havainnollisen käsityksen funktion raja-arvosta, jatkuvuudesta ja derivaatasta
- osaat määrittää yksinkertaisten funktioiden derivaatat
- osaat tutkia derivaatan avulla polynomifunktion kulkua ja määrittää sen ääriarvot
- tiedät, kuinka rationaalifunktion suurin ja pienin arvo määritetään
- osaat käyttää teknisiä apuvälineitä raja-arvon, jatkuvuuden ja derivaatan tutkimisessa ja rationaaliyhtälöiden ja -epäyhtälöiden ratkaisemisessa sekä polynomi- ja rationaalifunktion derivaatan määrittämisessä sovellusongelmissa.
Keskeiset sisällöt
- rationaaliyhtälö ja -epäyhtälö
- funktion raja-arvo, jatkuvuus ja derivaatta
- polynomifunktion, funktioiden tulon ja osamäärän derivoiminen
- polynomifunktion kulun tutkiminen ja ääriarvojen määrittäminen.
Opiskeluohjeita
Kurssimateriaali on jaettu kuuteen lukuun: Derivaatta, Raja-arvot ja jatkuvuus, Rationaalifunktiot, Derivointisääntöjä I, Funktion kulku sekä Derivointisääntöjä II.
Pääajatus kurssimateriaalissa on, että matematiikkaa oppii parhaiten tekemällä matematiikkaa. Materiaali on tämän vuoksi kirjoitettu niin, että teet tehtäviä käytännössä koko ajan. Jokainen luku sisältää kolme eri tehtäväsarjaa. Ensimmäisen tehtäväsarjan tehtävät ovat teorian seassa. Tarkoitus on, että etenet materiaalissa tekemällä jokaisen näistä tehtävistä. Voit hyvin tehdä tehtäviä yhdessä kaverin kanssa ja voit kysyä opettajalta heti, jos et ymmärrä jotain asiaa. Asia voi olla jokin tietty tehtävä, teoriassa oleva virke tai esimerkiksi vieras matemaattinen symboli. Pääasia on, että sinä itse teet tehtävät ja ymmärrät, mitä teet. Tämän tehtäväsarjan jälkeen kyseisen luvun teoria on käsitelty ja on aika harjoitella ja syventää juuri opittua. Ennen tätä opettaja pitää ehkä yhteisen opetustuokion tai -keskustelun, jossa pohditaan yhdessä luvun keskeisiä asioita tai työskentelyssä esiin tulleita haastavia kohtia. Mahdollisen opetustuokion jälkeen jatka harjoittelua luvun lopussa olevien kahden tehtäväsarjan tehtävien avulla. Luonnollisesti mitä enemmän harjoittelet, sitä paremmaksi tulet. Kun olet valmis, tee luvun lopussa oleva(t) itsearviointitesti(t). Niiden tarkoitus on kertoa sinulle, oletko ymmärtänyt luvun olennaiset asiat ja kehittää samalla oman oppimisesi arviointia, joka on tärkeä tulevaisuuden taito. Testeissä pärjääminen ei vielä tarkoita, että osaat luvun asiat esimerkiksi kiitettävällä tasolla, vaan testit keskittyvät vahvan perusosaamisen tutkimiseen. Ennen siirtymistä seuraavaan lukuun opettaja haluaa ehkä vielä koota luvussa opittuja asioita sekä antaa palautetta oppimisesta ja sen etenemisestä yhteisessä opetuskeskustelussa.
Kirje differentiaalilaskennan opiskelijalle
Keith Devlin on mm. Stanfordin yliopistossa vaikuttava matemaatikko, joka julkaisee kuukausittain tekstejä matematiikasta ja matematiikan oppimisesta blogissaan Devlin’s Angle. Kesäkuussa 2006, hän julkaisi kirjoituksen otsikolla Letter to a calculus student. Kirjoitus julkaistaan tässä suomennettuna hänen luvallaan. Kirjoitukseen ei päde CC-BY-AC-lisenssi. Alaviitteissä on joitakin huomioita tekstistä ja käännöksestä.
Kirje differentiaalilaskennan opiskelijalle
Hyvä differentiaalilaskennan opiskelija[1],
aloitan lainaamalla suurta filosofia Bertrand Russellia. Hän kirjoitti esseessään Mystiikka ja logiikka (1918): "Oikein nähtynä matematiikka sisältää paitsi totuuden myös äärimmäistä kauneutta — kylmää ja ankaraa kauneutta, sellaista kuin veistos edustaa, vetoamatta miltään osin luontomme vajavuuksiin, tukeutumatta musiikin tai taiteen suurellisiin hepeneisiin; silti ylevässä puhtaudessaan matematiikka pystyy tavoittamaan ankaran täydellisyyden, jota vain taiteista suurimmat edustavat."[2]
Kauneus on todennäköisesti yksi viimeisimpiä asioita joita yhdistät differentiaalilaskentaan. Voimaa, kyllä. Käyttökelpoisuutta, sitä myös. Toivottavasti myös nerokkuutta Newtonin ja Leibnizin osalta, jotka keksivät koko jutun. Todennäköisesti näet aiheen kokoelmana tekniikoita, joilla ratkotaan ongelmia, jotka liittyvät jatkuvaan muutokseen tai pinta-alojen ja tilavuuksien laskemiseen. Nämä tekniikat eroavat kaikesta siitä, mitä tähän asti olet matematiikassa kohdannut, joten näiden sääntöjen opettelu ja seuraaminen tulee vaatimaan sinulta paljon vaivaa ja keskittymistä. Näiden sääntöjen ymmärrys ja tieto siitä miksi ne pitävät paikkansa voi tulla vasta myöhemmin, jos silloinkaan. Aiheen sisäisen kauneuden arvostus tulee tätäkin myöhemmin. Jälleen, jos silloinkaan.
Pelkään, että tässä vaiheessa uraasi on epätodennäköistä, että voisit todella nähdä aiheen kauneuden. Kauneuden – todellisen, syvällisen kauneuden, ei pintakiiltoa – saavuttaa ainoastaan kokemuksella ja tuttuudella. Nähdäkseen ja arvostaakseen todellista kauneutta musiikissa meidän on kuunneltava paljon musiikkia – vielä parempaa on oppia soittamaan soitinta. Nähdäkseen syvällisen ja pinnan alla olevan kauneuden taiteessa meidän täytyy ensin katsella suurenmoisia maalauksia, ja parhaassa tapauksessa kokeilla omin käsin värin lisäämistä kankaalle. Vain kuluttamalla suuren määrän viiniä – monen vuoden saatossa, minun on lisättävä – saavutamme makuaistin jolla erotamme hyvän viinin. Ja vasta kun olemme seuranneet monta tuntia jalkapalloa, baseballia tai muuta urheilua, voimme todella arvostaa mestareiden taituruutta. Mestareiden toiminnan tai heidän luomuksien kauneuden kuvailun lukeminen ei voi koskaan muuta kuin vihjata mitä kirjoittaja yrittää välittää.
Tavoitteeni ei siis ole, että luet nämä sanani ja toteat, "Kyllä, nyt minä ymmärrän. Voi veljet, tämä Devlin-tyyppi on oikeassa. Differentiaalilaskenta on kaunista. Mahtavaa!" Mitä toivon on, että voin edes vakuuttaa sinut siitä, että minä (ja muut matemaatikot) voivat nähdä aiheen suuren kauneuden (mukaan luettuna differentiaalilaskennan). Ja ehkä jonain päivänä, monen vuoden päästä, jos jatkat matematiikan opiskelua, muistat lukeneesi nämä sanat, ja siinä tilanteessa nyökytät päätäsi tiedostaen ja ajattelet ”Kyllä, nyt minä näen mitä hän tarkoitti. Nyt minäkin osaan nähdä sen kauneuden".
Ensimmäinen askel kohti kauneuden näkemistä differentiaalilaskennassa – tai missään muussa matematiikan osa-alueessa – on ulottaa katse tekniikoiden ja symbolien manipuloinnin taakse ja nähdä aihe sellaisena kuin se on. Kuten shakespearelainen sonetti, joka vangitsee rakkauden todellisen olemuksen, tai maalaus joka tuo esiin ihmisen muodon kauneuden, joka on pintaa syvempää, niin differentiaalilaskennan todellista kauneutta voi vain täysin arvostaa menemällä tarpeeksi syvälle.
Differentiaalilaskennan kauneus on ensisijaisesti ideoissa. Ja differentiaalilaskennassa ei ole kauniimpaa ideaa kuin kaavassa, joka määrittää derivaatan: $$\text{(*) } f'(x) = \lim_{h \rightarrow 0}\frac{f(x+h) - f(x)}{h}$$ Jotta tässä olisi järkeä, niin on tärkeää, että $h$ ei ole yhtä kuin nolla. Sillä jos annat $h$:n olla nolla, niin edellisen kaavan osamäärästä tulee $$\frac{f(x+0) - f(x)}{0} = \frac{f(x) - f(x)}{0} = \frac{0}{0}$$ ja $\frac{0}{0}$ ei ole määritelty. Silti, jos otat minkä tahansa nollasta eroavan arvon $h$:lle, kuinka pienen tahansa, niin osamäärästä $$\frac{f(x+h) - f(x)}{h}$$ ei tule derivaatta (yleensä).
Joten mikä tarkkaan ottaen $h$ on? Vastaus on, että se ei ole luku, eikä se myöskään ole symboli, jolla merkitään tuntematonta lukua. Se on muuttuja.
Kysyt, mikä se semmoinen on? "Eikö muuttuja ole vain symboli, jolla merkitään tuntematonta lukua?" Vastaus on "Ei." Sir Isaac Newton ja Gottfried Leibniz, kaksikko joka keksi differentiaalilaskennan, tiesivät eron, mutta vaikuttaa siltä, että niinkin suuri ajattelija kuin kuuluisa 1700-luvun filosofi ja teologi (piispa) George Berkeley ei tiennyt. Traktaatissaan Analyytikko, uskottomalle matemaatikolle osoitettu tutkielma, Berkeley väittää, että vaikka differentiaalilaskenta johtaa tosiin lopputuloksiin, niin sen perusta on epävarma. Hän kirjoitti derivaatoista (joita Newton kutsui fluksioneiksi):
"Ja mitä ovat nämä fluksionit? Katoavien lisäyksien nopeus. Ja mitä ovat nämä samaiset katoavat lisäykset? Ne eivät ole äärellisiä suureita, taikka äärettömän pieniä suureita, eivätkä myöskään ei mitään. Emmekö voisi kutsua niitä kuolleiden suureiden haamuiksi?"[3]
"Katoavat lisäykset" joihin hän viittaa ovat nuo $h$:t kaavassa $(*)$. Berkeleyn ongelma – ja hän ei ollut missään mielessä yksin – oli, että hän ei kyennyt näkemään kaavan hienovaraisuutta[4]. Kuten mikä tahansa suuri taideteos, tämä kaava antaa samanaikaisesti erilaisia näkökulmia tarkastella samaa asiaa. Jos katsot sitä vain yhdestä näkökulmasta, niin menetät sen todellisen merkityksen. Se myös pyytää sinulta, ei, niin kuin kaikki suuret taideteokset, se haastaa sinut käyttämään mielikuvitustasi – mennä ohittaa aistikokemuksiesi ja astua idealisoituun maailman, jonka ihmismieli on luonnut.
Lauseke yhtäsuuruusmerkin oikealla puolella kaavassa $(*)$ edustaa prosessin tulosta. Ei prosessin jota voit suorittaa askel askeleelta, vaan idealisoidun, abstraktin prosessin, joka on olemassa ainoastaan mielessä. Tämä prosessi on suhteen $$\frac{f(x+h) - f(x)}{h}$$ laskeminen aina vain pienemmillä nollastapoikkeavilla $h$:n arvoilla ja sen yksikäsitteisen luvun tunnistaminen joita kohti nämä osamäärät lähestyvät, siinä mielessä, että näiden osamäärien ja tämän luvun välinen erotus voidaan tehdä niin pieneksi kuin halutaan valitsemalla $h$:lle tarpeeksi pieni arvo. (Derivaatan matemaattinen teoria on osaltaan sen päättelyä, milloin tällainen luku on olemassa, ja osoittaa, että mikäli se on olemassa, että se on yksikäsitteinen.) Syy miksi et varsinaisesti pysty suorittamaan tätä prosessia on se että se on ääretön: se pyytää sinua kuvittelemaan aina vain pienempien ja pienempien h:n arvojen ottamista ad infinitum[5].
Hienovaraisuus joka näyttää erehdyttäneen piispa Berkeley on, että vaikka alunperin ajattelemme $h$:n merkitsevän pienempiä ja pienempiä lukuja, niin "lim" termi kaavassa $(*)$ pyytää meitä ottamaan loikan (ja se on valtava) kuvitellaksemme ei ainoastaan osamäärän laskemista äärettömän monta kertaa, vaan koko prosessin tarkastelemista yhtenä kokonaisuutena. Se on itse asiassa henkeäsalpaava loikka.[6]
Runossa Viattomuuden tunnusmerkit, runoilija William Blake kirjoitti:
Nähdä maailma hiekanjyvässä
ja taivas kedon kukassa,
kannattaa kädessään äärettömyyttä
ja viettää ikuisuutta tunnissa[7]
Sitä kaava $(*)$ pyytää sinua tekemään: kannattaa äärettömyyttä kädessäsi. Nähdä äärettömän (ja siksi loppumattoman) prosessin yhtenä suoritettuna asiana. Onko mikään taideteos, mikään muu pala inhimillistä luovuutta, koskaan vaatinut niin paljon havainnoitsijaltaan? Ja johtanut niin valtavaan seuraukseen Ihmiskunnalle? Mikäli millään maalauksella, romaanilla, runolla tai veistoksella voidaan kuvitella olevan syvällistä kauneutta, niin voidaan oikeutetusti väittää, että derivaatan määritelmällä sitä on ylivoimaisesti enemmän.
Huomioita tekstistä ja käännöksestä
[1] Englanniksi otsikko on Letter to a calculus student. Calculus englanniksi vakiintunut lyhennelmä käsitteestä differential calculus. Suomeksi tällainen lyhennelmä ei ole vakiintunut, vaikka jossakin suomenkielisessä kirjallisuudessa puhutaan kalkyylistä. Differentiaalilaskenta on tietenkin vähän luotaantyöntävä termi - muutoslaskenta voisi olla nykykuulijalle olla helpommin lähestyttävä.
[2] Käännöksen lähde Wikipedia: Matematiikan kauneus.
[3] Tämä kappale voi antaa harhaanjohtavan kuvan Newtonin, Leibnizin ja Berkeleyn tiedoista. Newton ja Leibniz tosiaan kehittivät differentiaalilaskennasta toimivan matemaattisen menetelmän, mutta Berkeleyn kritiikki sen perustan epävarmuudelle oli aiheellinen. Lisäykset, toisella nimityksellä infinitesimaalit, joita differentiaalilaskenta hyödynsi ja Berkeley kritisoi, oli määritelty äärettömän pieniksi nollasta eroaviksi luvuiksi, joilla pystyi jakamaan, mutta jotka katosivat yhteen- ja vähennyslaskussa. Vasta 1800-luvulla Karl Weierstrass määritteli differentiaalilaskennan käsitteet uudelleen niin, ettei näitä infinitesimaaleja tarvittu. Vasta tällöin differentiaalilaskenta saatiin loogisesti pätevälle pohjalle. Keskeisin käsite, jota tällöin tarvittiin, oli raja-arvo.
Tarina ei pääty tähän. Kun Weierstrassin määritelmät tulivat tunnetuiksi, infinitesimaalin käsitettä pidettiin matematiikassa pitkään täysin tarpeettomana. Vuonna 1960 Abraham Robinson kuitenkin osoitti, että on määriteltävissä reaalilukujen joukkoa laajempi lukualue, hyperreaaliluvut, jossa on myös infinitesimaalisia lukuja. Tässä lukualueessa määritellään, että luku $x$ on infinitesimaalinen, jos se on pienempi kuin minkä tahansa positiivisen kokonaisluvun käänteisluku, mistä kuitenkaan ei seuraa, että se on tasan $0$. Tähän lukualueeseen perustuu Robinsonin kehittämä epästandardi analyysi, jonka avulla derivaatalle ja monille muille käsitteille voidaan esittää vaihtoehtoiset ja täysin täsmälliset määritelmät.
Kesti siis melkein 300 vuotta vastata Berkeleyn kritiikkiin.
Alaviitteen tekstin ja Berkeleyn tekstin käännöksen lähde Wikipedia: Hyperreaaliluku
[4] Berkeleyn kritiikki oli ihan oikeutettua ks. [3].
[5] ad infinitum on latinaa ja tarkoittaa ikuisesti, loputtomasti, äärettömästi, loputtomiin.
[6] Tämän suurenmoisen loikan teki vasta Weierstrass 1800-luvulla ks. [3].
[7] Perinteistä käännöstä on muutettu vaihtamalla sana loputtomuutta sanalla äärettömyyttä. Alkuperäisen käännöksen lähde on epäselvä.

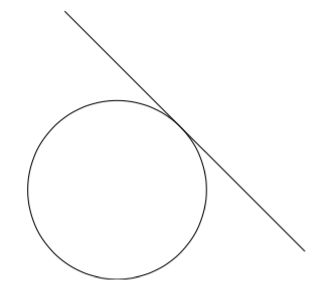
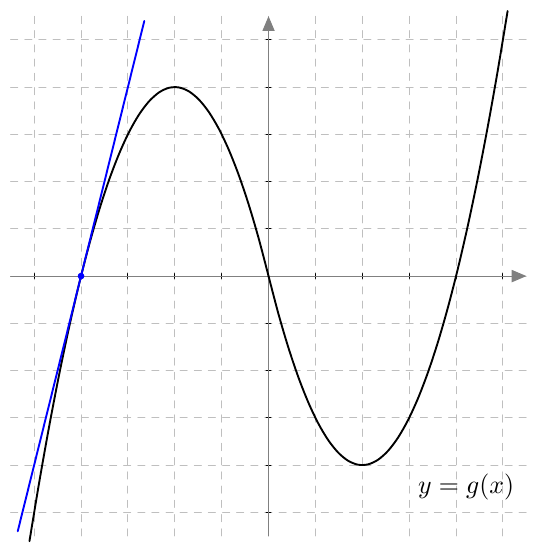
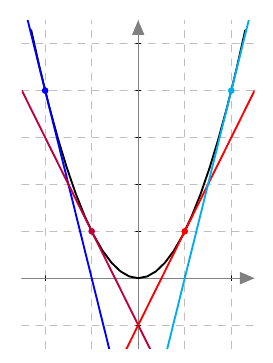
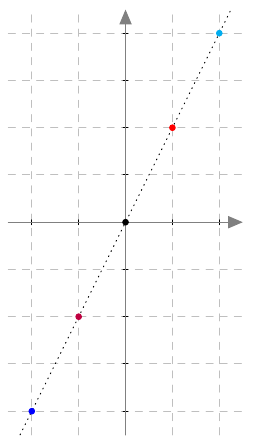
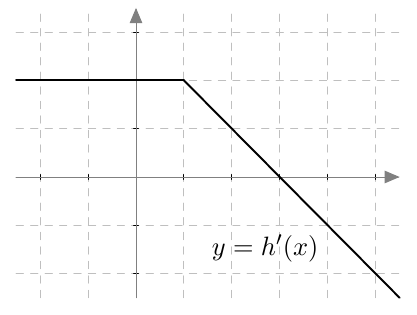
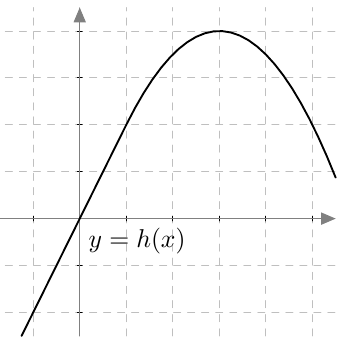
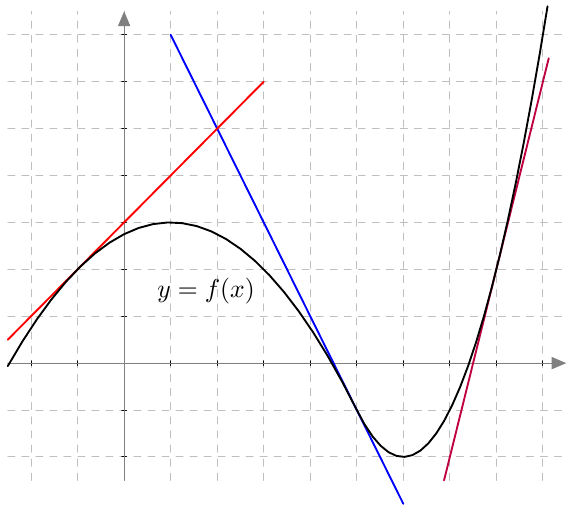
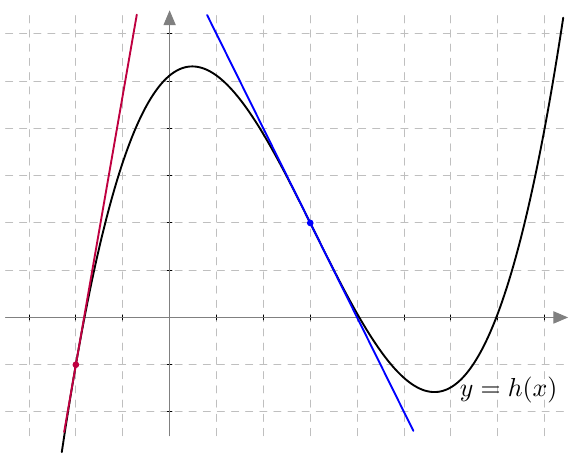
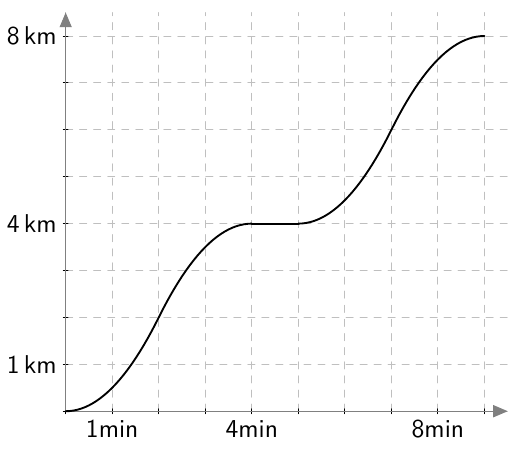
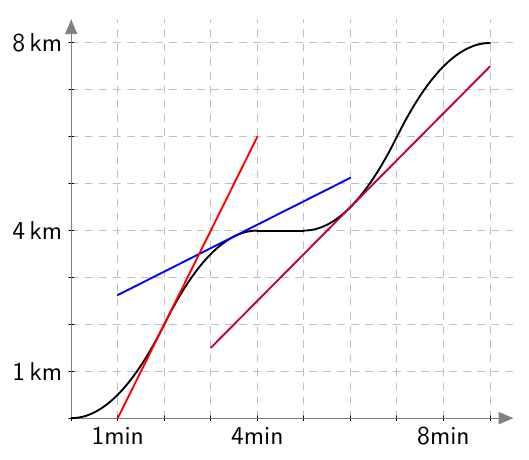

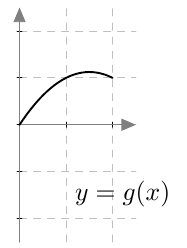
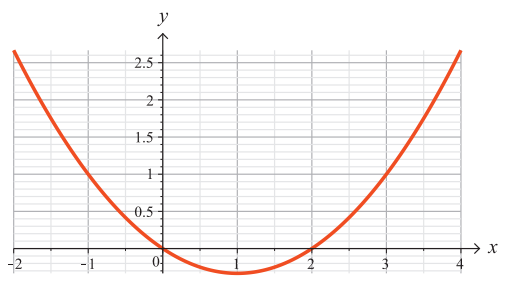
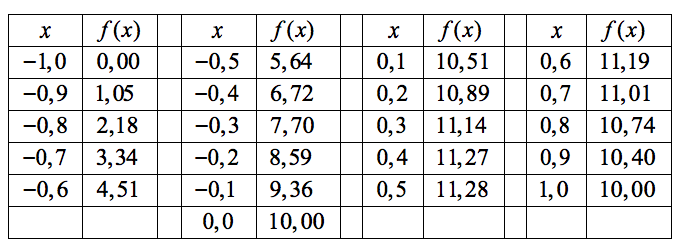
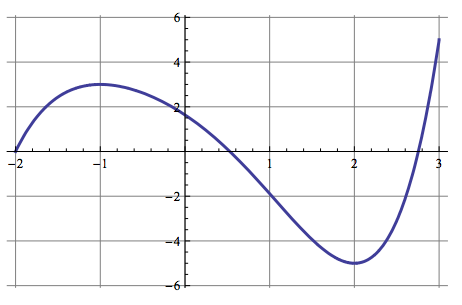
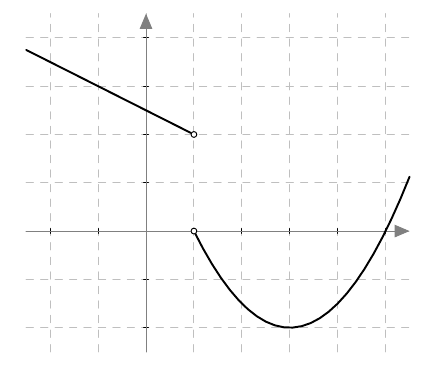
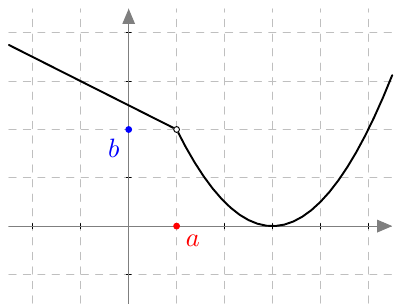
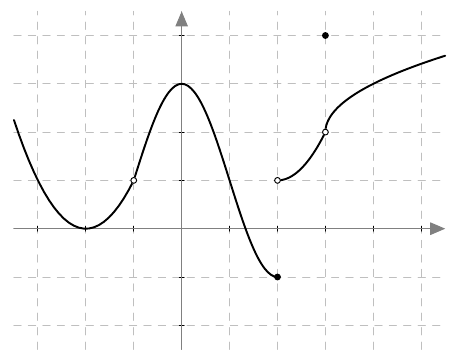
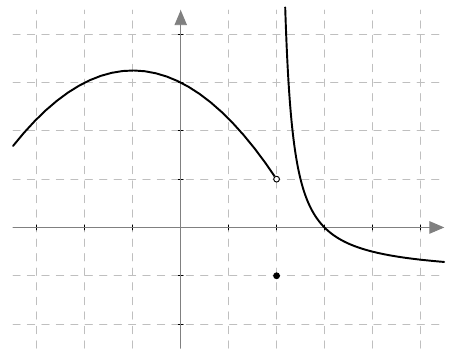
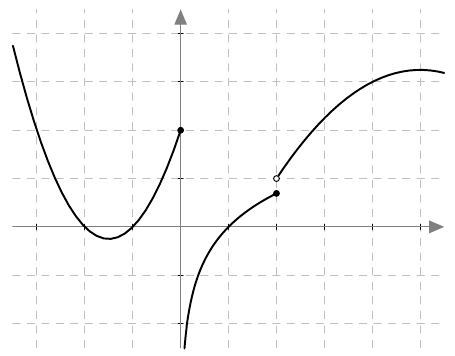


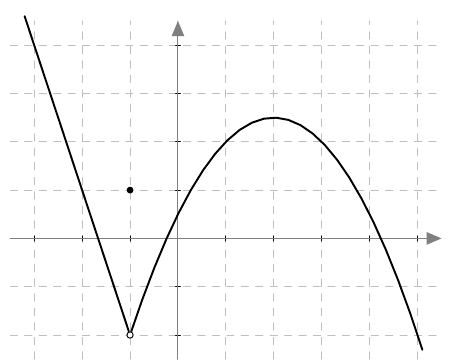
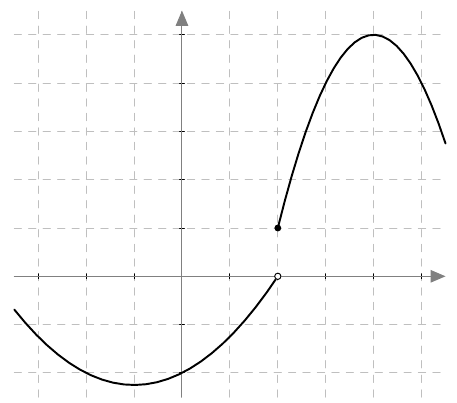
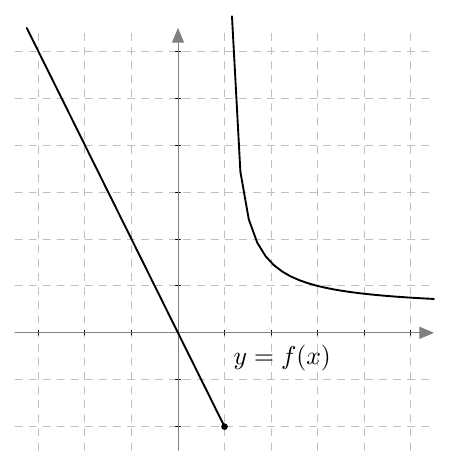
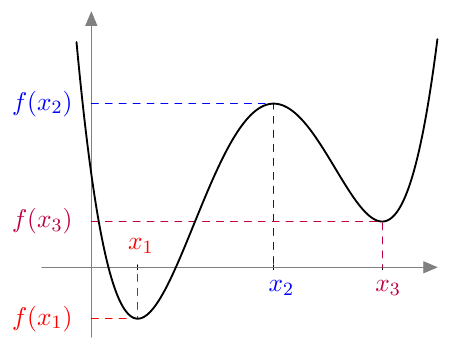
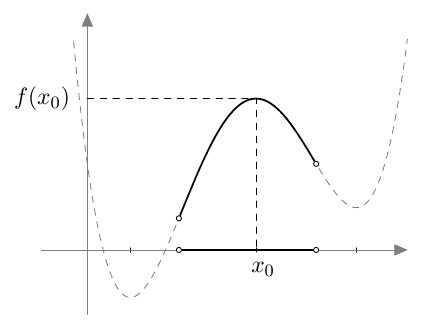
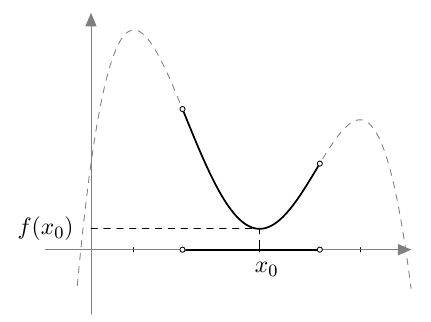
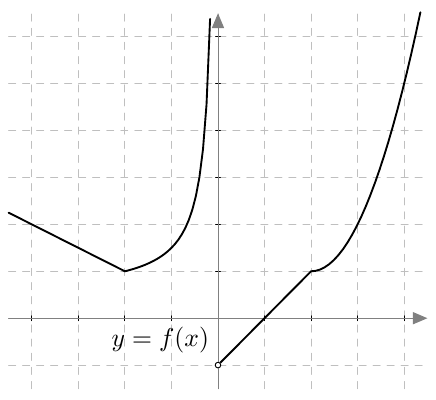
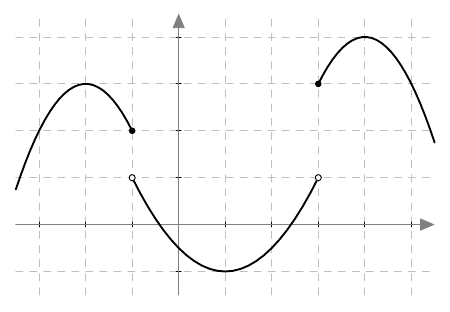 Onko funktio $g$ jatkuva välillä
Onko funktio $g$ jatkuva välillä 
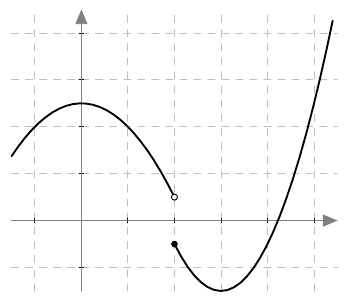
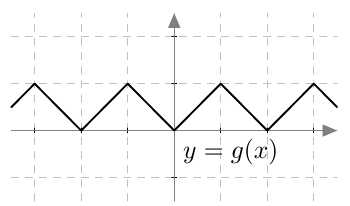
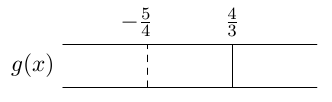
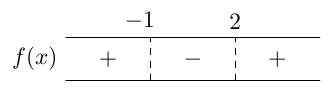
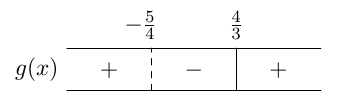 Funktio $g$ saa siis positiivisia arvoja lukusuoran väleillä $\pa -\infty, -\frac{5}{4} \pe$ ja $\pa \frac{4}{3}, \infty \pe$ ja negatiivisia arvoja lukusuoran välillä $\pa -\frac{5}{4}, \frac{4}{3} \pe$.
Funktio $g$ saa siis positiivisia arvoja lukusuoran väleillä $\pa -\infty, -\frac{5}{4} \pe$ ja $\pa \frac{4}{3}, \infty \pe$ ja negatiivisia arvoja lukusuoran välillä $\pa -\frac{5}{4}, \frac{4}{3} \pe$. 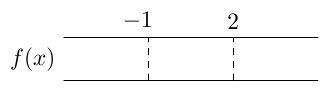
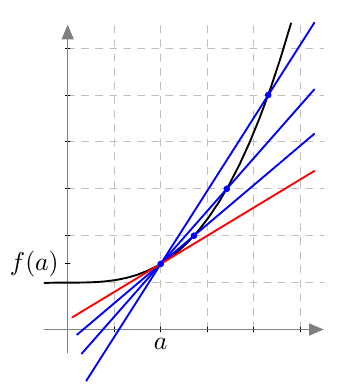
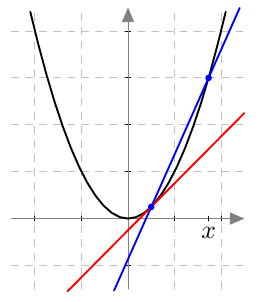
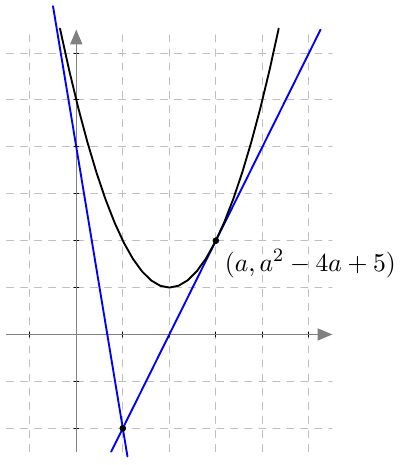
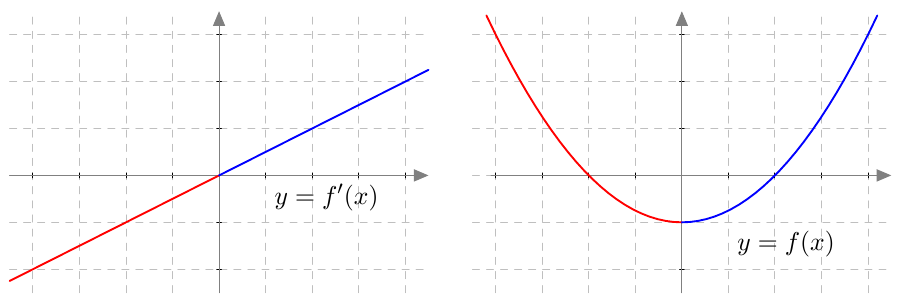
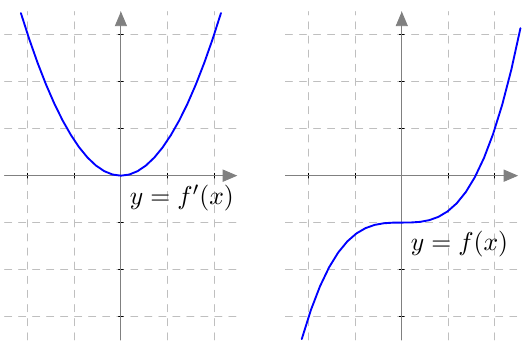
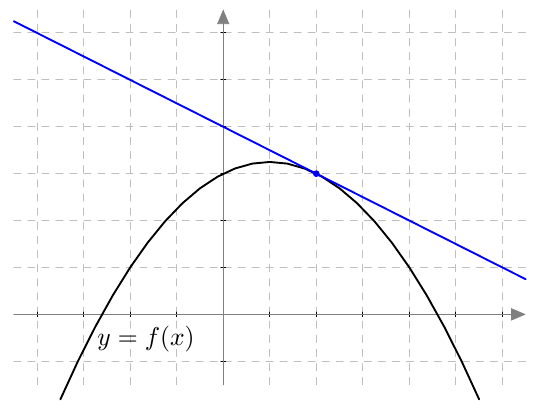
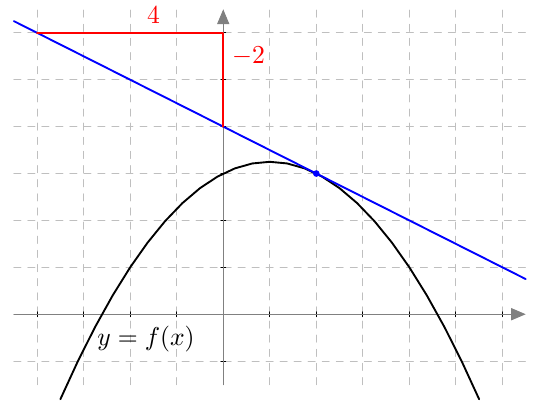
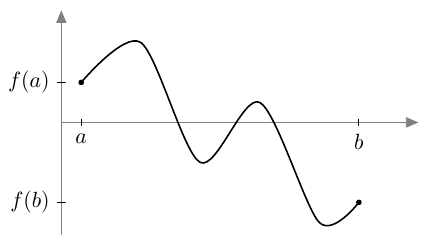
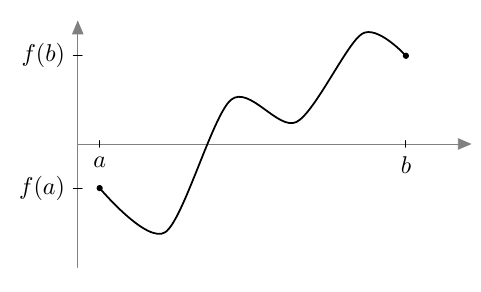
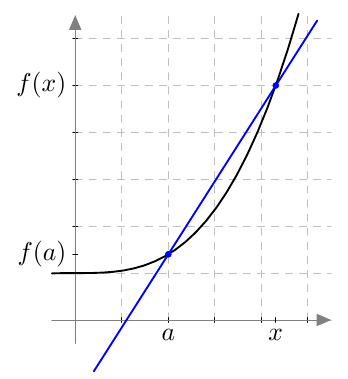 Tämän suoran kulmakerroin on $$ \frac{f(x) - f(a)}{x-a} $$ Sitä sanotaan funktion $f$ erotusosamääräksi kohdassa $a$.
Tämän suoran kulmakerroin on $$ \frac{f(x) - f(a)}{x-a} $$ Sitä sanotaan funktion $f$ erotusosamääräksi kohdassa $a$.