MAA5 - Analyyttinen geometria
Kurssin tavoitteet ja keskeiset sisällöt
Kurssin tavoitteena on, että
- ymmärrät, kuinka analyyttinen geometria luo yhteyksiä geometristen ja algebrallisten käsitteiden välille
- ymmärrät pistejoukon yhtälön käsitteen ja opit tutkimaan yhtälöiden avulla pisteitä, suoria, ympyröitä ja paraabeleja
- syvennät itseisarvokäsitteen ymmärtämystäsi ja opit ratkaisemaan sellaisia yksinkertaisia itseisarvoyhtälöitä ja vastaavia epäyhtälöitä, jotka ovat tyyppiä $|f(x)| = a$ tai $|f(x)| = |g(x)|$
- osaat käyttää teknisiä apuvälineitä pistejoukon yhtälön tutkimisessa sekä yhtälöiden, yhtälöryhmien, itseisarvoyhtälöiden ja epäyhtälöiden ratkaisemisessa sovellusongelmissa.
Keskeiset sisällöt
- pistejoukon yhtälö
- suoran, ympyrän ja paraabelin yhtälöt
- itseisarvoyhtälön ja epäyhtälön ratkaiseminen
- pisteen etäisyys suorasta.
Opiskeluohjeita
Kurssimateriaali on jaettu viiteen lukuun: Etäisyys, Suora, Ympyrä, Paraabeli ja muita pistejoukkoja sekä Itseisarvoyhtälö ja -epäyhtälö.
Pääajatus kurssimateriaalissa on, että matematiikkaa oppii parhaiten tekemällä matematiikkaa. Materiaali on tämän vuoksi kirjoitettu niin, että teet tehtäviä käytännössä koko ajan. Jokainen luku sisältää kolme eri tehtäväsarjaa. Ensimmäisen tehtäväsarjan tehtävät ovat teorian seassa. Tarkoitus on, että etenet materiaalissa tekemällä jokaisen näistä tehtävistä. Voit hyvin tehdä tehtäviä yhdessä kaverin kanssa ja voit kysyä opettajalta heti, jos et ymmärrä jotain asiaa. Asia voi olla jokin tietty tehtävä, teoriassa oleva virke tai esimerkiksi vieras matemaattinen symboli. Pääasia on, että sinä itse teet tehtävät ja ymmärrät, mitä teet. Tämän tehtäväsarjan jälkeen kyseisen luvun teoria on käsitelty ja on aika harjoitella ja syventää juuri opittua. Ennen tätä opettaja pitää ehkä yhteisen opetustuokion tai -keskustelun, jossa pohditaan yhdessä luvun keskeisiä asioita tai työskentelyssä esiin tulleita haastavia kohtia. Mahdollisen opetustuokion jälkeen jatka harjoittelua luvun lopussa olevien kahden tehtäväsarjan tehtävien avulla. Luonnollisesti mitä enemmän harjoittelet, sitä paremmaksi tulet. Kun olet valmis, tee luvun lopussa oleva(t) itsearviointitesti(t). Niiden tarkoitus on kertoa sinulle, oletko ymmärtänyt luvun olennaiset asiat ja kehittää samalla oman oppimisesi arviointia, joka on tärkeä tulevaisuuden taito. Testeissä pärjääminen ei vielä tarkoita, että osaat luvun asiat esimerkiksi kiitettävällä tasolla, vaan testit keskittyvät vahvan perusosaamisen tutkimiseen. Ennen siirtymistä seuraavaan lukuun opettaja haluaa ehkä vielä koota luvussa opittuja asioita sekä antaa palautetta oppimisesta ja sen etenemisestä yhteisessä opetuskeskustelussa.

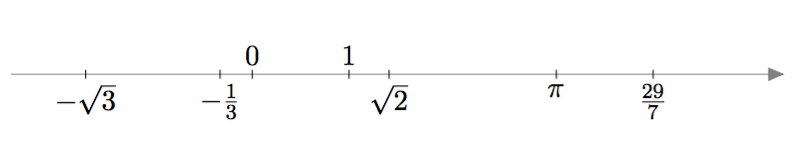
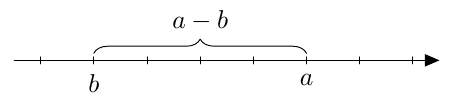 Toisaalta erotus $a-b$ on positiivinen, joten $\left|a-b\right| = a-b$.
Toisaalta erotus $a-b$ on positiivinen, joten $\left|a-b\right| = a-b$. 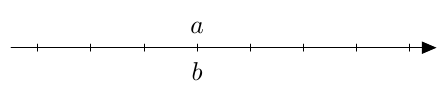 Toisaalta erotus $a - b = 0$, joten $\left|a-b\right| = \left|0\right| = 0$.
Toisaalta erotus $a - b = 0$, joten $\left|a-b\right| = \left|0\right| = 0$. 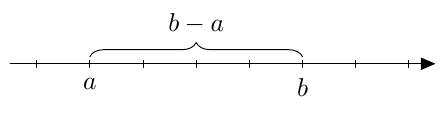 Toisaalta erotus $a-b$ on negatiivinen, joten \begin{align*} \left|a-b\right| &= -(a-b) \\ &= -a+b \\ &= b-a. \end{align*}
Toisaalta erotus $a-b$ on negatiivinen, joten \begin{align*} \left|a-b\right| &= -(a-b) \\ &= -a+b \\ &= b-a. \end{align*} 
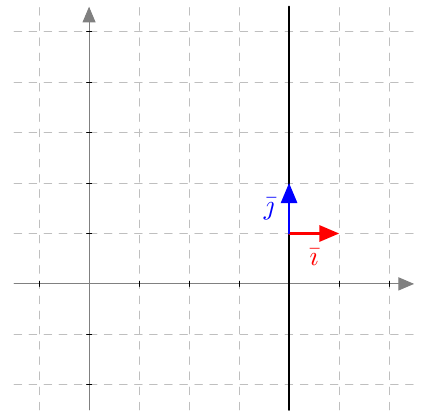
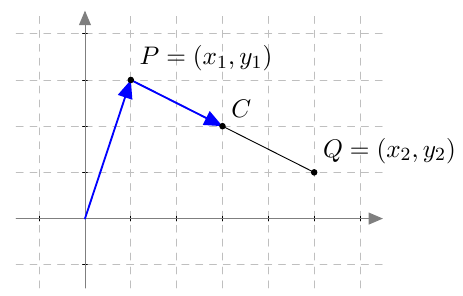 Kun siihen sijoitetaan \begin{align*} \pv{OP} &= x_1\vi + y_1\vj \\ \pv{PQ} &= (x_2-x_1)\vi + (y_2-y_1)\vj, \end{align*} paikkavektoriksi saadaan sievennyksen jälkeen \begin{align*} \pv{OC} &= \frac{1}{2}(x_1+x_2)\vi + \frac{1}{2}(y_1 + y_2)\vj. \end{align*} Paikkavektorista voidaan lukea pisteen $C$ koordinaatit. Siis $$ C = \left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right). $$
Kun siihen sijoitetaan \begin{align*} \pv{OP} &= x_1\vi + y_1\vj \\ \pv{PQ} &= (x_2-x_1)\vi + (y_2-y_1)\vj, \end{align*} paikkavektoriksi saadaan sievennyksen jälkeen \begin{align*} \pv{OC} &= \frac{1}{2}(x_1+x_2)\vi + \frac{1}{2}(y_1 + y_2)\vj. \end{align*} Paikkavektorista voidaan lukea pisteen $C$ koordinaatit. Siis $$ C = \left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right). $$ 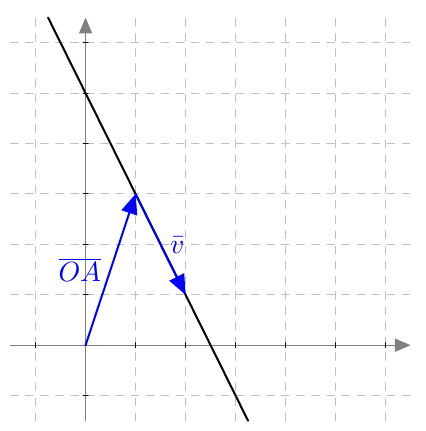
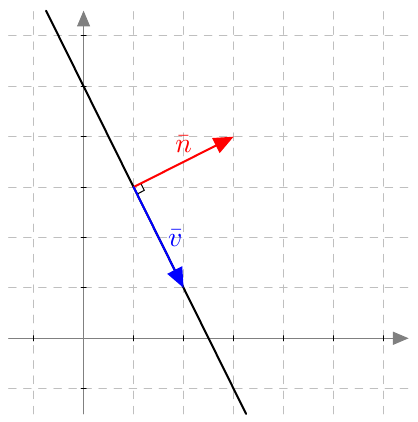
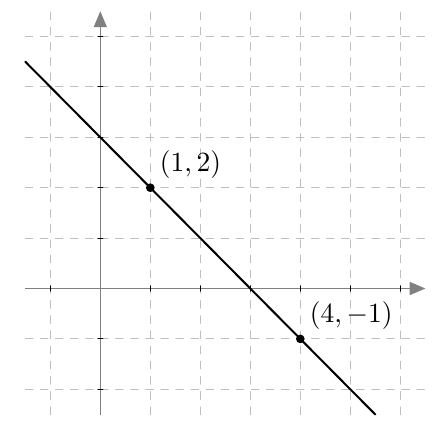
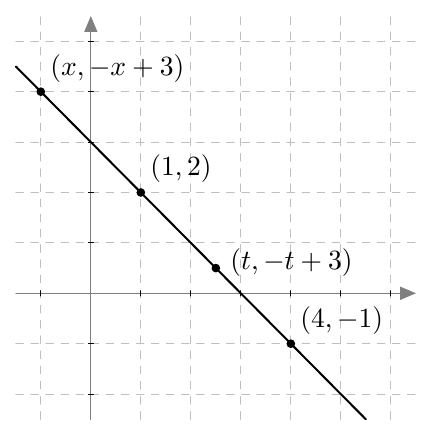

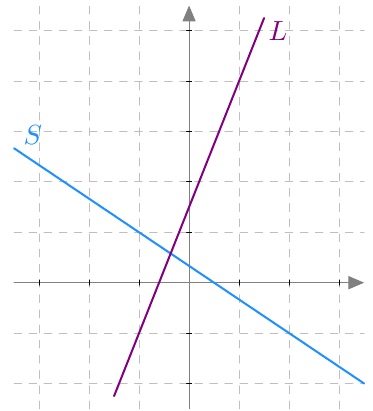
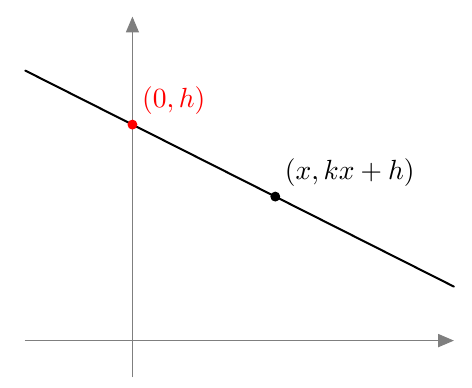
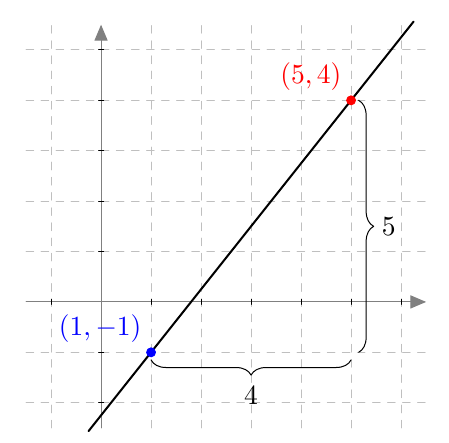
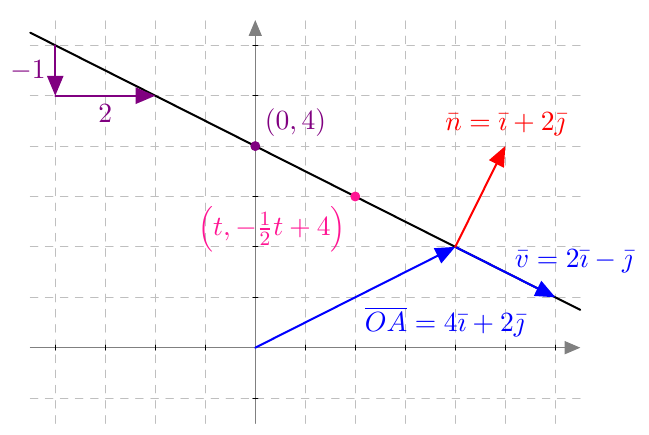
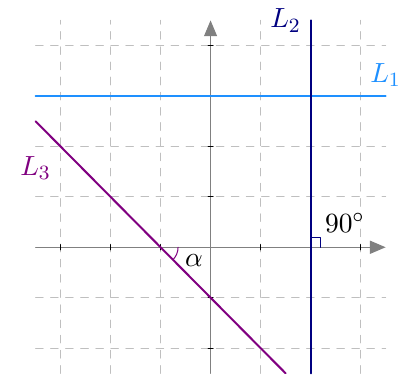
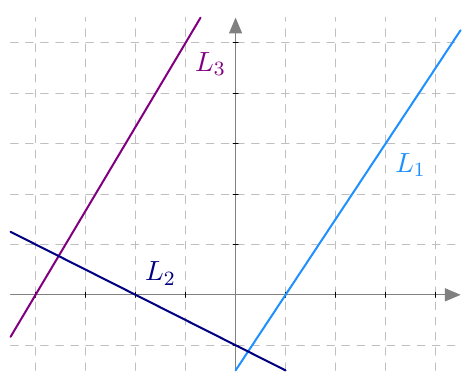
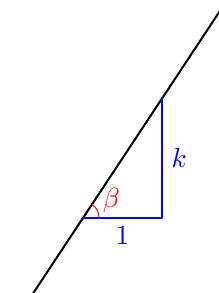
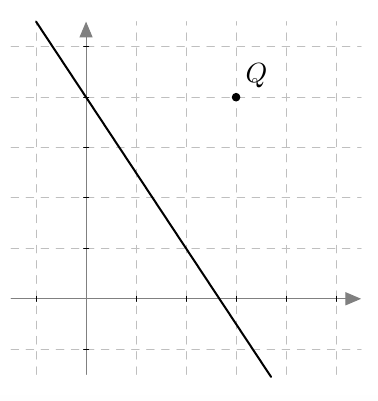
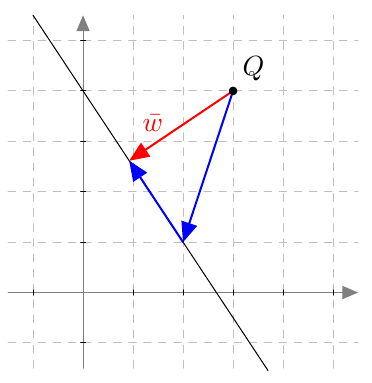
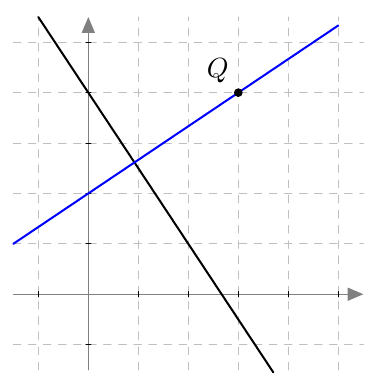
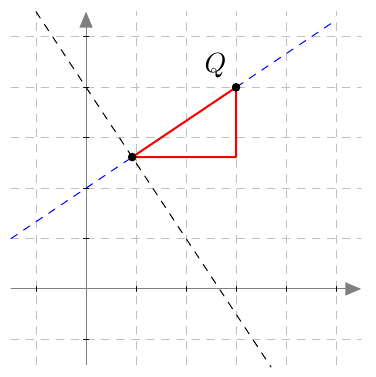
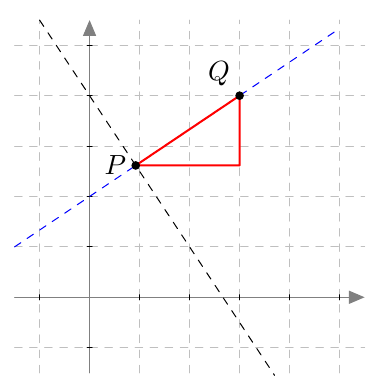
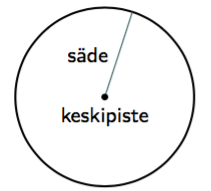
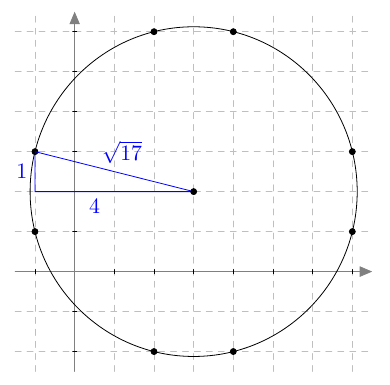
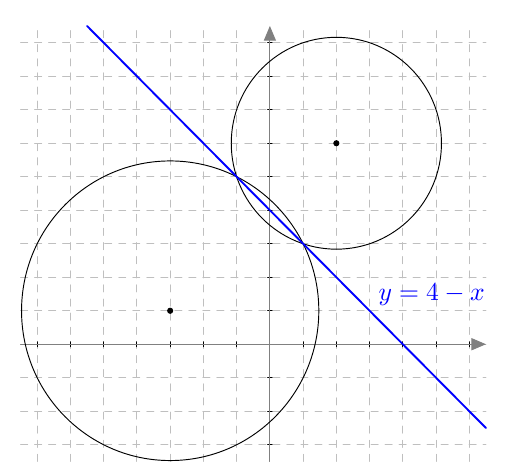

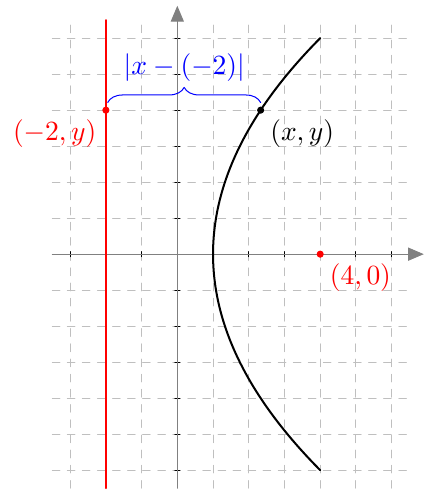 Piste $(x,y)$ on paraabelin piste, jos ja vain jos sen etäisyydet polttopisteeseen ja johtosuoraan ovat yhtä suuret eli yhtälö $$ \sqrt{(x-4)^2 + y^2} = \left| x+2\right| \tag{A} $$ toteutuu.
Piste $(x,y)$ on paraabelin piste, jos ja vain jos sen etäisyydet polttopisteeseen ja johtosuoraan ovat yhtä suuret eli yhtälö $$ \sqrt{(x-4)^2 + y^2} = \left| x+2\right| \tag{A} $$ toteutuu. 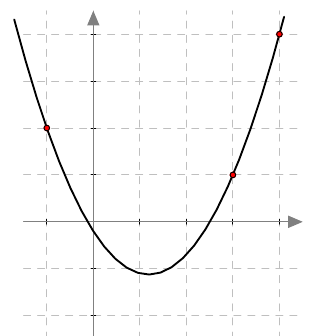
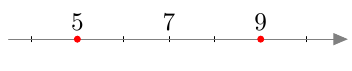
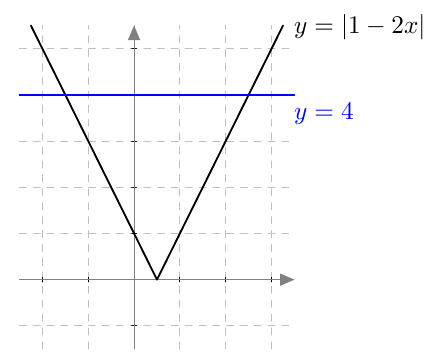
 Yhtälö siis toteutuu, jos ja vain jos $$-4 < x \quad \textbf{ ja } \quad x < 8.$$ Tämä voidaan ilmaista myös kaksoisepäyhtälönä $-4 < x < 8$.
Yhtälö siis toteutuu, jos ja vain jos $$-4 < x \quad \textbf{ ja } \quad x < 8.$$ Tämä voidaan ilmaista myös kaksoisepäyhtälönä $-4 < x < 8$.  Yhtälö siis toteutuu, jos ja vain jos $$x < -2 \quad \textbf{ tai } \quad x > 6.$$
Yhtälö siis toteutuu, jos ja vain jos $$x < -2 \quad \textbf{ tai } \quad x > 6.$$ 
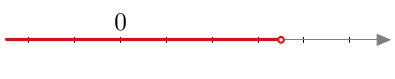
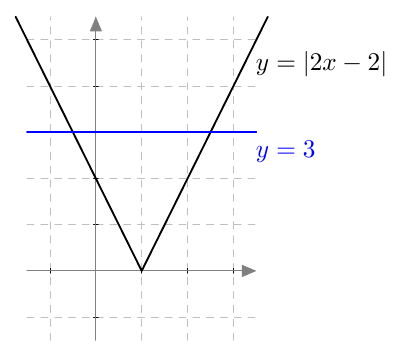
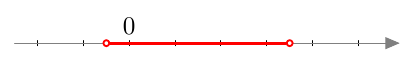 Epäyhtälön $\left|2x - 3 \right| < 4$ ratkaisujoukko on siis lukusuoran väli $$\left] -\frac{1}{2}, \frac{7}{2}\right[.$$ Hakasulkujen suunnasta näkyy, että välin päätepisteet eivät kuulu ratkaisujoukkoon.
Epäyhtälön $\left|2x - 3 \right| < 4$ ratkaisujoukko on siis lukusuoran väli $$\left] -\frac{1}{2}, \frac{7}{2}\right[.$$ Hakasulkujen suunnasta näkyy, että välin päätepisteet eivät kuulu ratkaisujoukkoon. 

 Kaksiosainen ratkaisujoukko voidaan merkitä yhdisteen merkin $\displaystyle \cup$ avulla seuraavasti: $$\left] -\infty, -2\right] \cup \left[-\frac{1}{3}, \infty\right[.$$ Hakasulkujen suunnasta näkyy, että päätepisteet $-2$ ja $-\frac{1}{3}$ kuuluvat ratkaisujoukkoon.
Kaksiosainen ratkaisujoukko voidaan merkitä yhdisteen merkin $\displaystyle \cup$ avulla seuraavasti: $$\left] -\infty, -2\right] \cup \left[-\frac{1}{3}, \infty\right[.$$ Hakasulkujen suunnasta näkyy, että päätepisteet $-2$ ja $-\frac{1}{3}$ kuuluvat ratkaisujoukkoon.