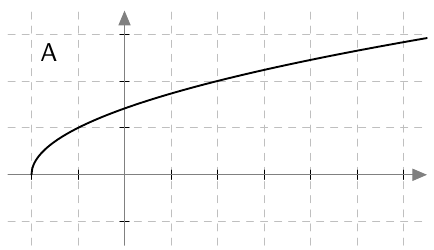
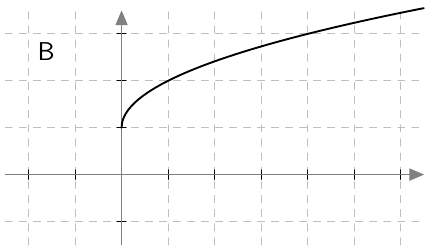
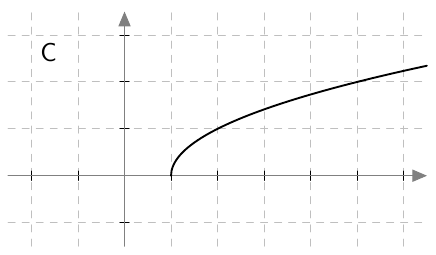
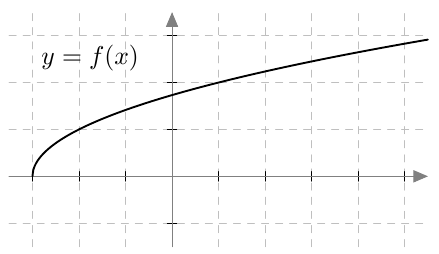
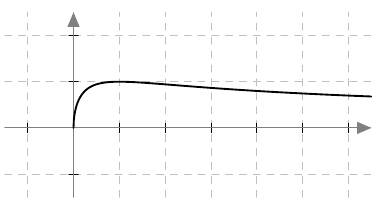
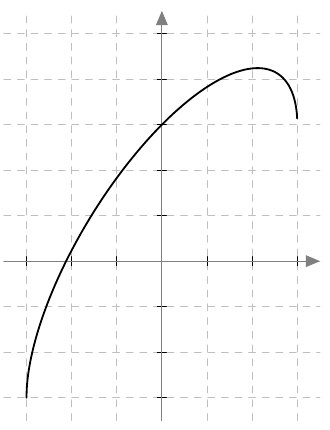
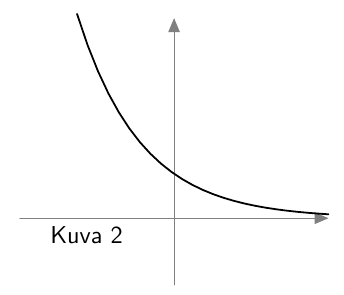
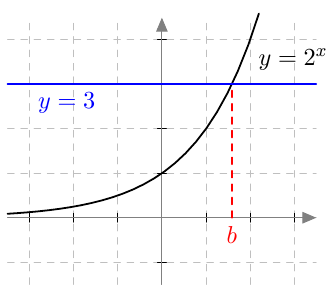
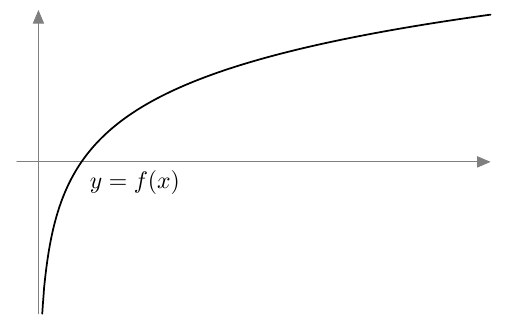
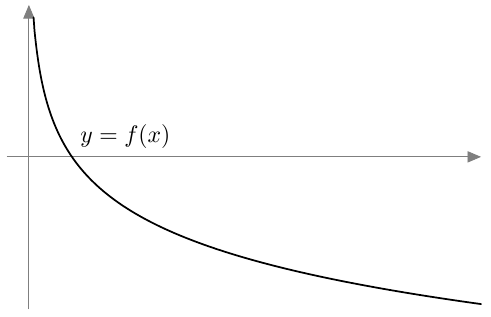
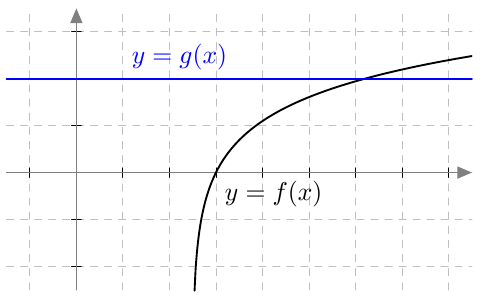
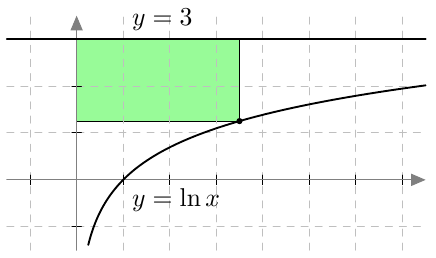
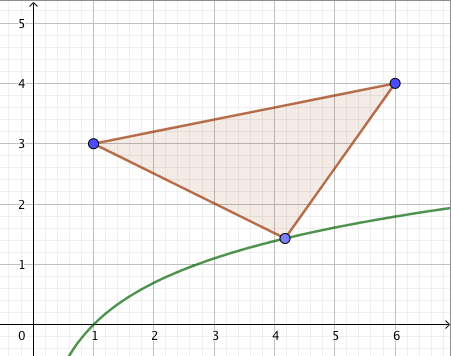
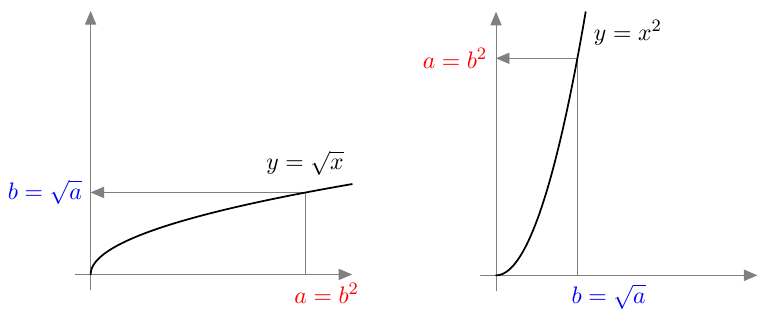
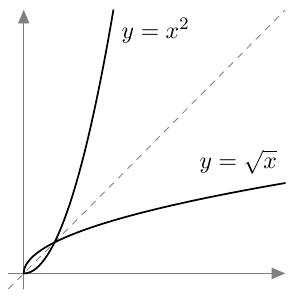
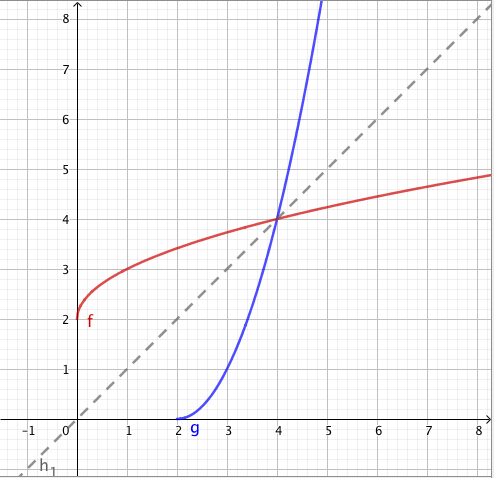
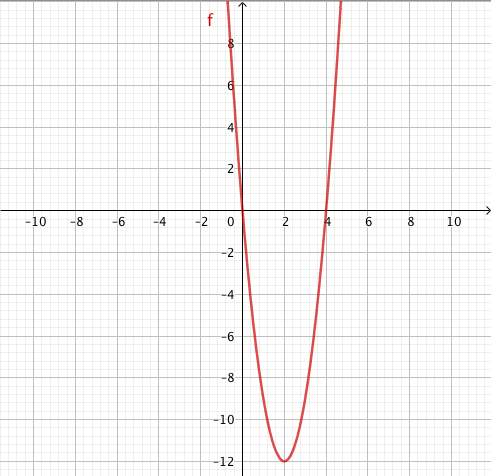
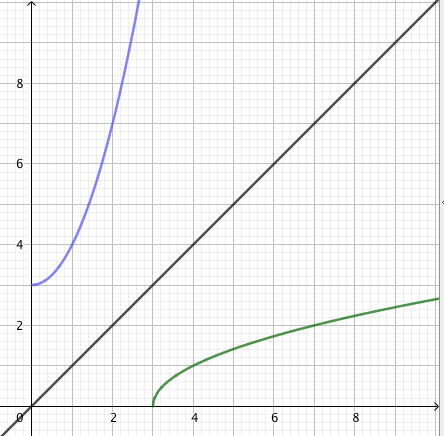
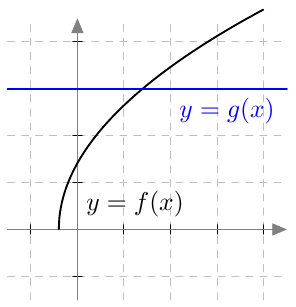
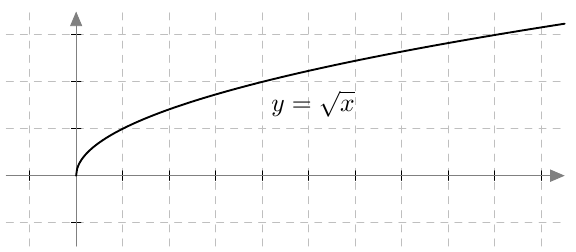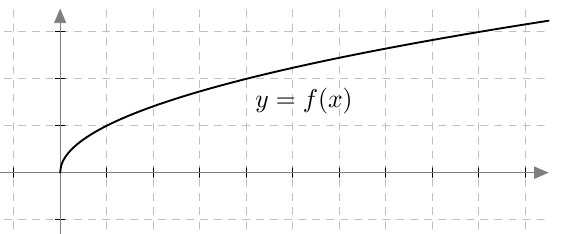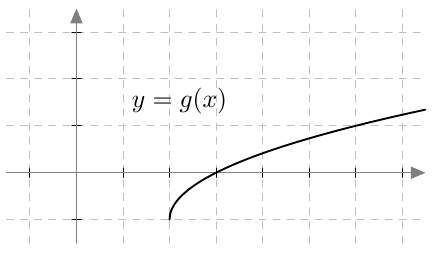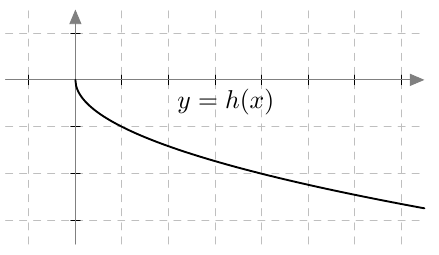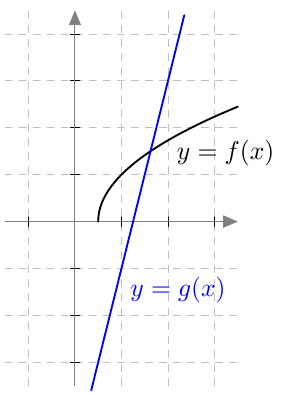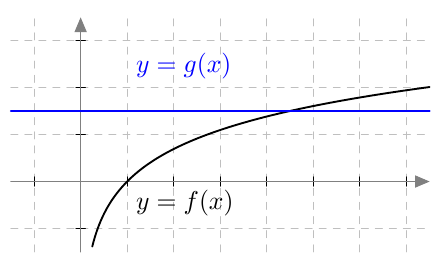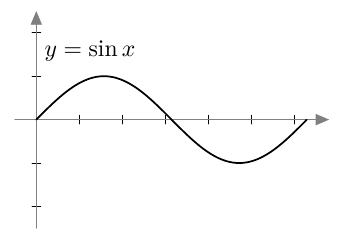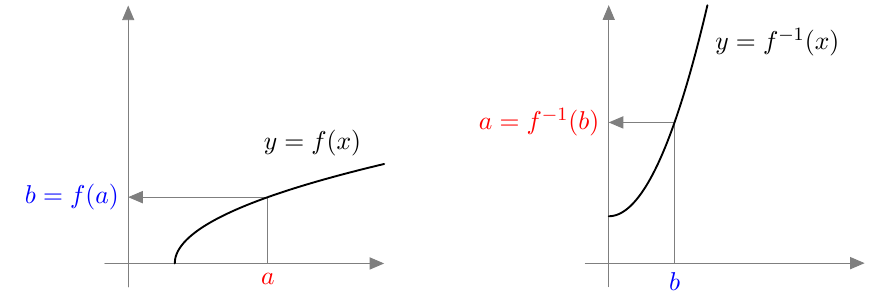Kun tutkitaan, missä kohdassa jokin juurifunktio saa tietyn arvon, päädytään niin sanottuun juuriyhtälöön. Esimerkiksi jos halutaan tietää, missä kohdassa funktio $$f(x) = \sqrt{4x+3}$$ saa arvon $4$, joudutaan tutkimaan yhtälöä $$f(x) = 4$$ eli yhtälöä $$\sqrt{4x+3} = 4.$$ Tätä yhtälöä voidaan havainnollistaa piirtämällä juurifunktion $f(x) = \sqrt{4x+3}$ kuvaaja ja vakiofunktion $g(x) = 4$ kuvaaja samaan koordinaatistoon:
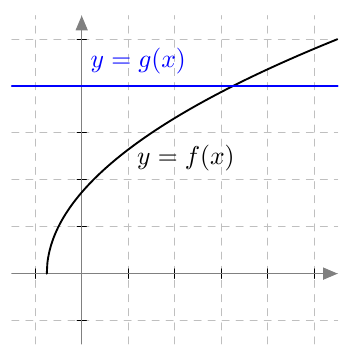
Piirroksesta nähdään, että kuvaajat leikkaavat yhdessä kohdassa eli yhtälöllä on täsmälleen yksi ratkaisu $x \approx 3$. (Tähän päätelmään tarvitaan toki myös tieto siitä, että neliöjuurifunktio saa aina vain suurempia arvoja juurrettavan kasvaessa. Muuten kuvan ulkopuolella voisi olla lisää leikkauskohtia.)
Ratkaisun tarkan arvon selvittäminen ei onnistu pelkän piirroksen avulla vaan tarvitaan muita keinoja. Määritelmän mukaan neliöjuuri on luku, jonka toinen potenssi on sama kuin juurrettava: $$ \left(\sqrt{a}\right)^2 = a $$ kaikilla $a \geq 0$. Neliöjuuresta päästään siis eroon, kun yhtälön kumpikin puoli korotetaan toiseen potenssiin: \begin{align*} \sqrt{4x + 3} &= 4 \quad \mid (\phantom{1})^2 \\ \left(\sqrt{4x + 3}\right)^2 &= 4^2 \\ 4x + 3 &= 16 \\ 4x &= 13 \\ x &= \frac{13}{4} = 3{,}25 \end{align*} Yhtälön ratkaisu on siis $x = 3{,}25$.
Ratkaise yhtälö $$ \sqrt{5x + 2} = 3 $$ samaan tapaan kuin edellä tehtiin. Tarkista vastauksen järkevyys piirtämällä samaan koordinaatistoon funktioiden $f(x) = \sqrt{5x + 2}$ ja $g(x) = 3$ kuvaajat esimerkiksi Geogebralla.
Yhtälö toteutuu, jos ja vain jos $$x = \dfrac{7}{5} = 1{,}4.$$ Kuvasta nähdään, että tulos on järkevä:
Toiseen potenssiin korotuksen käyttö yhtälöiden ratkaisussa poikkeaa aikaisemmin käytetyistä peruslaskutoimituksista. Yhteenlaskun voi aina kumota vähennyslaskulla ja kääntäen. Nollasta poikkeavalla luvulla kertomisen voi aina kumota jakolaskulla, ja jakolaskun voi kumota kertolaskulla. Toiseen potenssiin korotusta ei kuitenkaan voi kumota niin, että varmasti päästäisiin takaisin samaan yhtälöön, josta lähdettiin.
Jos esimerkiksi yhtälön $x = 2$ molemmat puolet korotetaan toiseen potenssiin, saadaan yhtälö $x^2 = 4$. Symbolien avulla ilmaistuna $$ x = 2 \Rightarrow x^2 = 4. $$ Yhtälöstä $x^2 = 4$ ei kuitenkaan voida varmasti päätellä, että $x = 2$, sillä myös $(-2)^2 = 4$. Toisin sanottuna $$ x^2 = 4 \not\Rightarrow x = 2. $$ Oikea päätelmä tässä tapauksessa on $$ x^2 = 4 \Rightarrow x = 2 \ \text{ tai } \ x = -2. $$
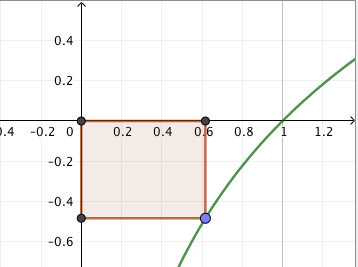
Toiseen potenssiin korotus auttaa pääsemään neliöjuurista eroon, mutta saattaa yllä mainitun ilmiön vuoksi tuottaa "ratkaisuja", jotka eivät todellisuudessa ole yhtälön ratkaisuja. Esimerkiksi jos ratkaistaan yhtälö $$ \sqrt{4x + 3} = -1 $$ samaan tapaan kuin edellä, saadaan seuraava päättelyketju: \begin{align*} \sqrt{4x + 3} &= -1 \quad \mid (\phantom{1})^2 \\ \left(\sqrt{4x + 3}\right)^2 &= (-1)^2 \\ 4x + 3 &= 1 \\ 4x &= -2 \\ x &= -\frac{1}{2} = -0{,}5 \end{align*} Jos ratkaisun olemassaoloa tutkitaan graafisesti, paljastuu kuitenkin, että yhtälöllä ei ole yhtään ratkaisua:
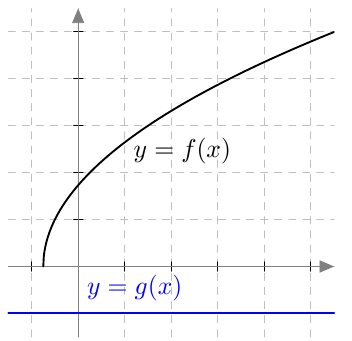
Päättelyssä ei sinänsä ole mitään vikaa: se osoittaa, että jos yhtälöllä $\sqrt{4x + 3} = -1$ olisi ratkaisu, se olisi $x = -0{,}5$; mikään muu luku ei voisi tulla kysymykseen. Toiseen potenssiin korotusta voi siis huoletta käyttää neliöjuuriyhtälöiden ratkaisemiseen, kunhan muistaa lopuksi tarkistaa, ovatko löytyneet ratkaisuehdokkaat oikeasti ratkaisuja. Tässäkin tapauksessa sijoittamalla huomataan, että $x = -0{,}5$ ei ole yhtälön ratkaisu. Nimittäin jos $x = -0{,}5$, niin yhtälön vasemmaksi puoleksi saadaan \begin{align*} \sqrt{4\cdot (-0{,}5) + 3} &= \sqrt{-2 + 3} \\ &= \sqrt{1} \\ &= 1. \end{align*} Yhtälön vasen ja oikea puoli eivät siis ole yhtä suuria.
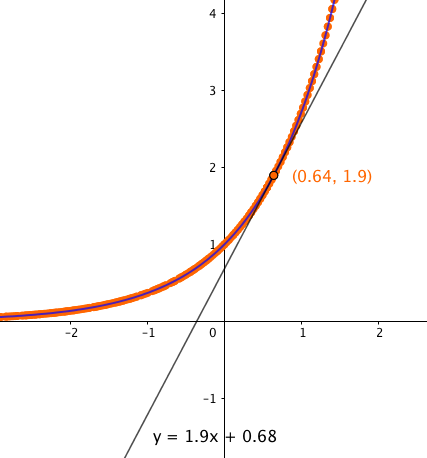
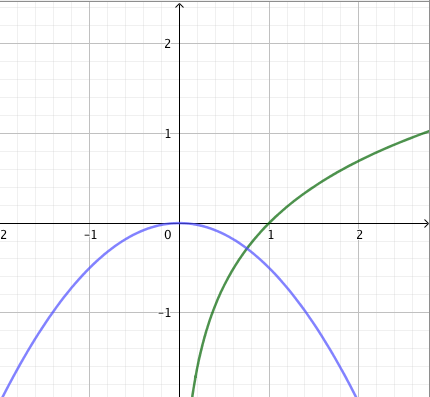
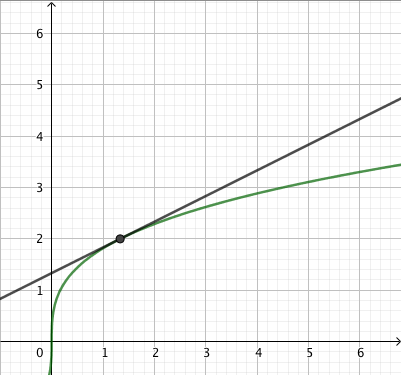
Tehtävänä on ratkaista yhtälö $$ \sqrt{x} = 2x-3. $$
- Hahmottele samaan koordinaatistoon funktioiden $f(x) = \sqrt{x}\,$ ja $g(x) = 2x - 3$ kuvaajat. Kuinka monta ratkaisua tutkittavalla yhtälöllä näyttää olevan?
- Ratkaise yhtälö korottamalla molemmat puolet toiseen potenssiin. Muista tutkia sijoittamalla, ovatko kaikki ratkaisuehdokkaat todella yhtälön ratkaisuja.
Vinkki: kertaa tarvittaessa summan ja erotuksen neliön kaavat MAA2-kurssin teoreemasta 3.
- Yhtälöllä näyttää olevan täsmälleen yksi ratkaisu:
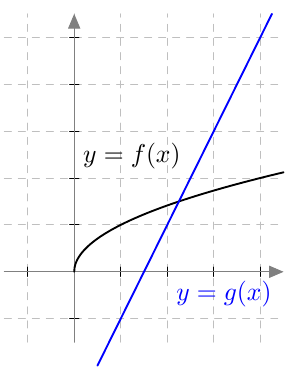
- Yhtälöstä $$ x = (2x-3)^2 $$ saadaan ratkaisuehdokkaat $x_1 = 1$ ja $x_2 = \frac{9}{4}$.
Sijoittamalla huomataan, että ehdokas $x_1$ ei toteuta alkuperäistä yhtälöä: jos $x = 1$, niin yhtälön vasen puoli on $\sqrt{1} = 1$ mutta oikea puoli on $2\cdot 1 - 3 = 2-3 = -1$.
Ehdokas $x_2$ puolestaan toteuttaa alkuperäisen yhtälön: jos $x = \frac{9}{4}$, niin yhtälön vasen puoli on $$ \sqrt{\frac{9}{4}} = \frac{3}{2} $$ ja oikea puoli on $$ 2\cdot \frac{9}{4} - 3 = \frac{9}{2} - \frac{6}{2} = \frac{3}{2}. $$ Yhtälö $$ \sqrt{x} = 2x-3 $$ siis toteutuu, jos ja vain jos $x = \dfrac{9}{4}$.
Se, että kaikki ratkaisuehdokkaat eivät kelpaa neliöjuuriyhtälön ratkaisuksi, juontaa juurensa neliöjuuren määritelmään. Neliöjuuren määritelmän mukaan luvun neliöjuuri on aina epänegatiivinen: $$ \sqrt{a} \geq 0 $$ kaikilla $a \geq 0$. Tämän tiedon avulla voidaan jo etukäteen päätellä, mitkä luvut eivät ainakaan kelpaa neliöjuuriyhtälön ratkaisuiksi. Esimerkiksi aiemmin tutkitun yhtälön $$ \sqrt{4x+3} = -1 $$ tapauksessa voidaan päätellä, että sen vasen ja oikea puoli ovat erimerkkiset muuttujan $x$ arvosta riippumatta: vasen puoli on aina epänegatiivinen ja oikea puoli on aina negatiivinen. Yhtälöllä ei siten ole yhtään ratkaisua.
Onko seuraavilla yhtälöillä ratkaisuja? Päättele ensin ja tarkista päättelysi piirtämällä funktioiden kuvaajat samaan koordinaatistoon esimerkiksi Geogebralla.
- $\sqrt{7-x} = -4$
- $\sqrt{3x-5} = -x^2-1$
- Yhtälöllä ei ole yhtään ratkaisua, koska sen vasen puoli on aina epänegatiivinen ja oikea puoli on aina negatiivinen. Vasen ja oikea puoli ovat siis erimerkkiset riippumatta muuttujan $x$ arvosta.
- Yhtälöllä ei ole yhtään ratkaisua, koska sen vasen ja oikea puoli ovat erimerkkiset riippumatta muuttujan $x$ arvosta. Yhtälön vasen puoli on neliöjuurena aina epänegatiivinen. Yhtälön oikea puoli on aina negatiivinen. Tämä seuraa siitä, että $x^2 \geq 0$ kaikilla reaaliluvuilla $x$: \begin{align*} x^2 &\geq 0 \\ -x^2 &\leq 0 \\ -x^2 - 1 &\leq -1. \end{align*}
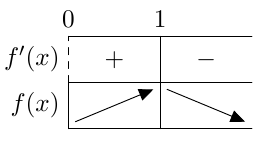
Tehtävän 1.11 yhtälön $$ \sqrt{x} = 2x-3. $$ tapauksessa tilanne on mutkikkaampi. Sen vasen puoli on neliöjuuren määritelmän nojalla aina epänegatiivinen, mutta oikean puolen merkki riippuu muuttujasta $x$. Yhtälö voi toteutua vain, jos myös oikea puoli on epänegatiivinen eli $2x - 3 \geq 0$. Kun tämä epäyhtälö ratkaistaan, saadaan ehto mahdollisille ratkaisuille: \begin{align*} 2x - 3 &\geq 0\\[1.5mm] 2x &\geq 3 \\[1.5mm] x &\geq \frac{3}{2} \end{align*} Tätä ehtoa kutsutaan neliöönkorotusehdoksi ja sen avulla voidaan tehtävässä 1.11 löydetyistä ratkaisuehdokkaista poimia todelliset ratkaisut: ehdokas $x_1 = 1$ ei toteuta neliöönkorotusehtoa $x \geq 1{,}5$ mutta ehdokas $x_2 = 2{,}25$ toteuttaa sen. Yhtälöllä on siis täsmälleen yksi ratkaisu, joka on $x = 2{,}25$.
Tehtävänä on ratkaista yhtälö $$ \sqrt{2x-1} = 4x-5. $$
- Mikä ehto yhtälön oikean puolen pitää toteuttaa, että yhtälö voi toteutua? Muodosta ja kirjaa ylös tämä neliöönkorotusehto.
Vinkki: mitä voit sanoa yhtälön vasemman puolen merkistä? - Ratkaise yhtälö normaaliin tapaan korottamalla kumpikin puoli toiseen potenssiin. Karsi valeratkaisut todellisista ratkaisuista a-kohdan neliöönkorotusehdon avulla.
- Piirrä samaan koordinaatistoon funktioiden $f(x) = \sqrt{2x-1}$ ja $g(x) = 4x-5$ kuvaajat esimerkiksi Geogebralla. Varmista kuvasta, että kaikki valeratkaisut saatiin todella karsittua pois.
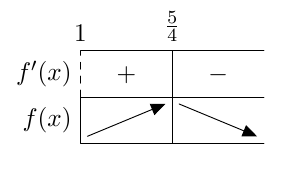
- Neliöönkorotusehto on $4x - 5 \geq 0$ eli $$ x \geq \frac{5}{4}. $$ Koska yhtälön $$ \sqrt{2x-1} = 4x-5. $$ vasen puoli on neliöjuurena aina epänegatiivinen, täytyy yhtälön oikeankin puolen olla epänegatiivinen, jotta yhtälö voi toteutua.
- Yhtälöstä $$ 2x - 1 = (4x-5)^2 $$ saadaan ratkaisuehdokkaat $x_1 = \frac{13}{8} = 1{,}625$ ja $x_2 = 1$. Näistä neliöönkorotusehdon $x \geq 1{,}25$ toteuttaa vain ehdokas $x_1$. Yhtälö $$\sqrt{2x-1} = 4x-5$$ siis toteutuu, jos ja vain jos $$x = \frac{13}{8}.$$
- Kuvaajilla on yksi leikkauskohta, joten yhtälöllä on yksi ratkaisu:
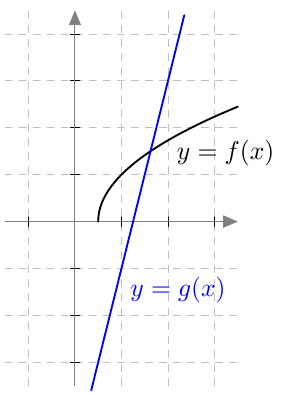
Kaikki valeratkaisut saatiin siis karsittua pois.
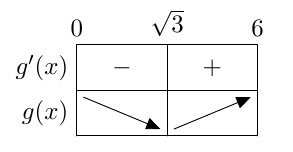
Neliöönkorotusehto muodostetaan tutkimalla, millä ehdolla yhtälön vasen ja oikea puoli ovat saman merkkisiä. Aina sekään ei riitä sulkemaan kaikkia valeratkaisuja pois. Esimerkiksi yhtälön $$ \sqrt{x^2 - 1} = \sqrt{2x - 1\phantom{ {}^2 }} $$ kumpikin puoli on aina epänegatiivinen, joten mitään neliönkorotusehtoa ei ole. Päätellään samaan tapaan kuin edellä: \begin{align*} \sqrt{x^2 - 1} &= \sqrt{2x - 1\phantom{ {}^2 }} \quad \mid (\phantom{1})^2 \\ x^2 - 1 &= 2x - 1 \\[1mm] x^2 - 2x &= 0 \\[1mm] x(x-2) &= 0 \\[1mm] x = 0 \ &\text{ tai } \ x = 2 \end{align*} Jos ratkaisut tarkistaa sijoittamalla alkuperäiseen yhtälöön, huomaa, että joukkoon on kuitenkin jälleen soluttautunut valeratkaisu. Nimittäin jos $x = 0$, niin alkuperäisen yhtälön vasen puoli on $$ \sqrt{x^2 - 1} = \sqrt{0^2-1} = \sqrt{-1}, $$ joka ei ole määritelty. Ehdokas $x = 0$ ei siis kelpaa ratkaisuksi. Jos $x = 2$, alkuperäisen yhtälön vasen puoli on $$ \sqrt{x^2 - 1} = \sqrt{2^2-1} = \sqrt{3} $$ ja oikea puoli on $$ \sqrt{2x - 1} = \sqrt{2\cdot 2 - 1} = \sqrt{3}. $$ Alkuperäisellä yhtälöllä on siis täsmälleen yksi ratkaisu $x = 2$.
Neliöönkorotuksen avulla muodostettu uusi yhtälö voi siis tuottaa myös sellaisia valeratkaisuja, joilla alkuperäinen neliöjuuriyhtälö ei ole määritelty. Kaikkien valeratkaisujen tunnistamiseksi pitää neliöönkorotusehdon lisäksi tutkia, millä ehdoilla yhtälö on määritelty. Aikaisemmissa tehtävissä on kuvaajien avulla varmistettu, että valeratkaisut on saatu karsittua pois. Joissakin tilanteissa kuvaajan piirtäminen voi kuitenkin olla hyvin hankalaa. Tarvitaan siis menetelmä, jolla ratkaisut saadaan selvitettyä myös silloin, kun kuvaajia ei voi käyttää päättelyn tukena.
Tehtävänä on ratkaista yhtälö $$ \sqrt{x^2 + 2x - 15} = \sqrt{3x-13}. $$
- Millä ehdolla yhtälön vasen puoli on määritelty?
Vinkki: kertaa tarvittaessa toisen asteen epäyhtälön ratkaiseminen MAA2-kurssin luvusta 3. - Millä ehdolla yhtälön oikea puoli on määritelty?
- Liittykö yhtälöön neliöönkorotusehtoa?
- Yhdistä edellisten kohtien ehdot yhdeksi ehdoksi, joka yhtälön ratkaisujen pitää toteuttaa.
- Ratkaise yhtälö normaaliin tapaan korottamalla kumpikin puoli toiseen potenssiin. Karsi valeratkaisut pois d-kohdan ehdon avulla.
- Yhtälön vasen puoli on määritelty, jos ja vain jos $x \leq -5$ tai $x \geq 3$.
- Yhtälön oikea puoli on määritelty, jos ja vain jos $x \geq \frac{13}{3} \approx 4{,}33$.
- Yhtälön kumpikin puoli on epänegatiivinen kaikilla muuttujan arvoilla, joten yhtälöön ei liity neliöönkorotusehtoa.
- Yhtälön ratkaisujen pitää toteuttaa ehto $x \geq \frac{13}{3}$.
- Yhtälöstä $$ x^2 + 2x - 15 = 3x - 13 $$ saadaan ratkaisuehdokkaat $x_1 = -1$ ja $x_2 = 2$. Kumpikaan niistä ei toteuta d-kohdassa muodostettua ehtoa, joten yhtälöllä ei ole yhtään ratkaisua.
Jos kaikkien neliöönkorotus- ja määrittelyehtojen tutkiminen tuntuu liian työläältä, toinen vaihtoehto on seuloa todelliset ratkaisut valeratkaisuista sijoittamalla kaikki ratkaisuehdokkaat alkuperäiseen yhtälöön. Sijoittamalla tarkistaminen toimii aina. Neliöjuuriyhtälön ratkaisemiseksi on siis kaksi tapaa:
- Neliöönkorotus ja tarkistus sjoittamalla:
- Hankkiudu eroon neliöjuurista korottamalla yhtälön kumpikin puoli toiseen potenssiin.
- Ratkaise näin saamasi yhtälö normaalisti.
- Tutki alkuperäiseen yhtälöön sijoittamalla, mitkä ratkaisuehdokkaista ovat todellisia ratkaisuja.
- Määrittely- ja neliöönkorotusehtojen avulla:
- Kirjaa ylös ehdot, joilla yhtälö on määritelty.
- Muodosta neliöönkorotusehto päättelemällä, millä ehdolla yhtälön vasen ja oikea puoli ovat saman merkkiset.
- Hankkiudu eroon neliöjuurista korottamalla yhtälön kumpikin puoli toiseen potenssiin.
- Ratkaise näin saamasi yhtälö normaalisti.
- Päättele määrittely- ja neliöönkorotusehtojen avulla, mitkä ratkaisuehdokkaista ovat todellisia ratkaisuja.
- Valitse jompi kumpi edellä mainituista ratkaisutavoista ja ratkaise yhtälö $$ 2\sqrt{x} = 3-x. $$
- Kumpi ratkaisutavoista miellyttää sinua enemmän? Miksi? Kerro omin sanoin.
- Ratkaisuehdokkaiksi saadaan $x_1 = 1$ ja $x_2 = 9$. Alkuperäinen yhtälö toteutuu, jos ja vain jos $x = 1$.
Ratkaise seuraavat neliöjuuriyhtälöt. Ennen kuin korotat yhtälön molemmat puolet toiseen potenssiin, muokkaa yhtälöä niin, että neliöjuuren sisältävä termi on yksinään yhtälön toisella puolella.
- $x - \sqrt{x + 2} = 0$
- $1 + \sqrt{x-1} = x$
- $x = 2$
- $x = 1$ tai $x = 2$
Tarkastellaan tämän kappaleen lopuksi vielä korkeampien juuriyhtälöiden ratkaisemista. Jos yhtälössä esiintyy $n$:s juuri, voi ratkaisussa käyttää potenssiin $n$ korotusta. Muut huomioitavat asiat riippuvat siitä, onko kysymyksessä pariton vai parillinen juuri.
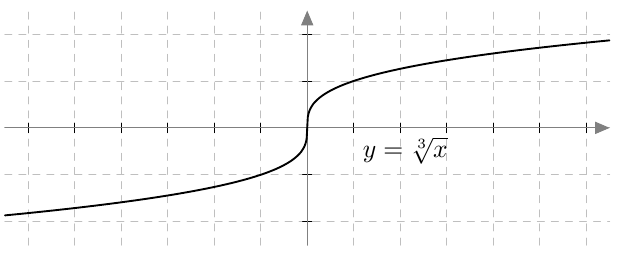
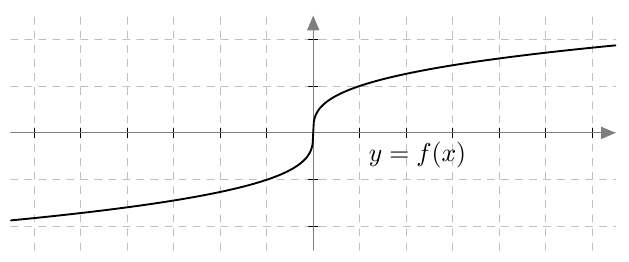
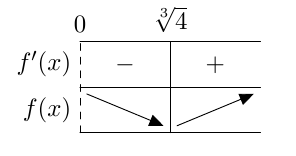
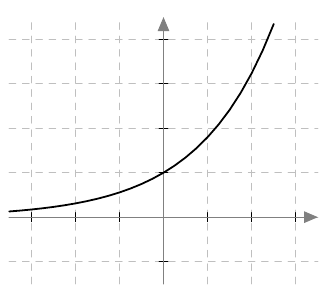
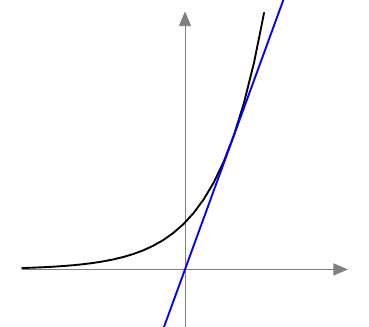
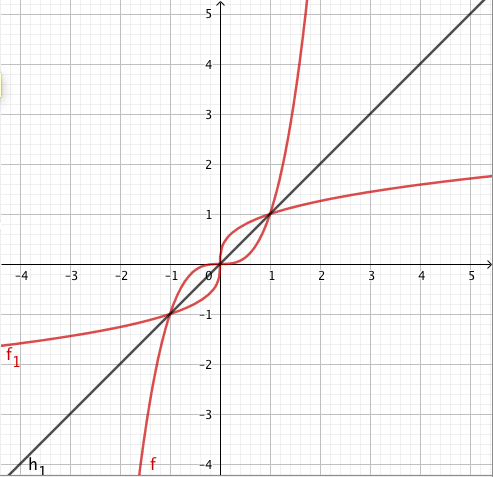
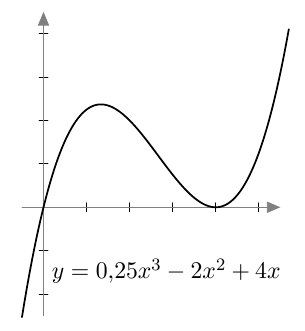
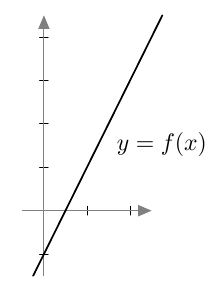
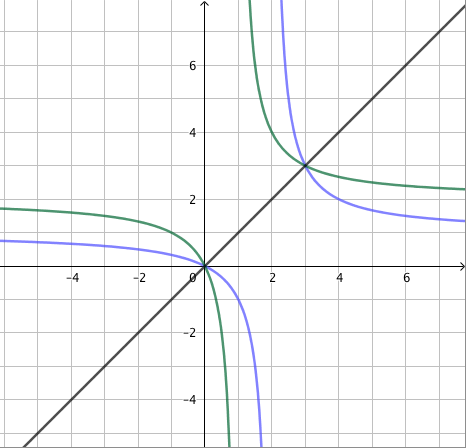
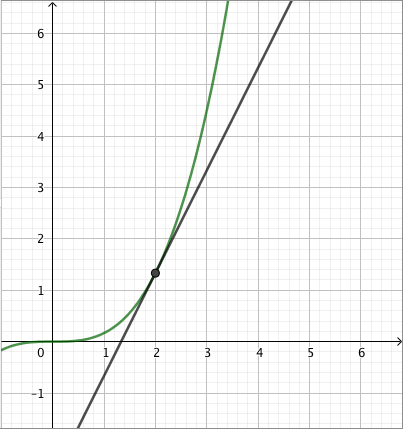
Jos yhtälössä esiintyy pariton juuri, esimerkiksi kuutiojuuri tai viides juuri, valeratkaisuista ei tarvitse huolehtia. Tämä johtuu siitä, että parittomat potenssifunktiot saavat jokaisen arvonsa vain kerran. Esimerkiksi alla olevasta kolmannen asteen potenssifunktion kuvaajasta nähdään, että $$ x = \sqrt[3]{2} \Rightarrow x^3 = 2 $$ ja $$ x^3 = 2 \Rightarrow x = \sqrt[3]{2}. $$ 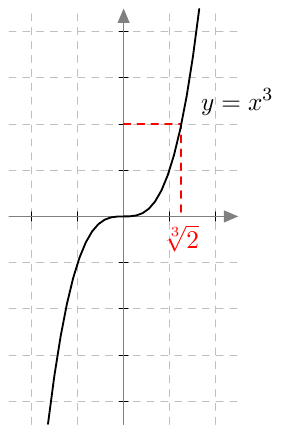
Jos yhtälön molemmat puolet korotetaan parittomaan potenssiin, on uusi yhtälö siis yhtäpitävä alkuperäisen yhtälön kanssa, sillä parittomaan potenssiin korotus voidaan kumota ottamalla yhtälön molemmista puolista vastaava $n$:s juuri.
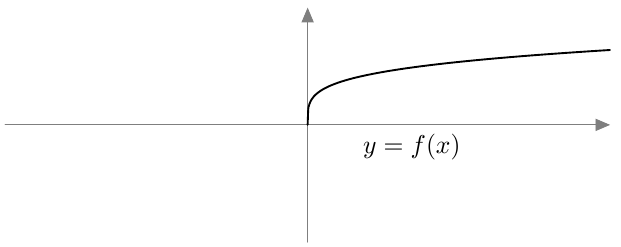
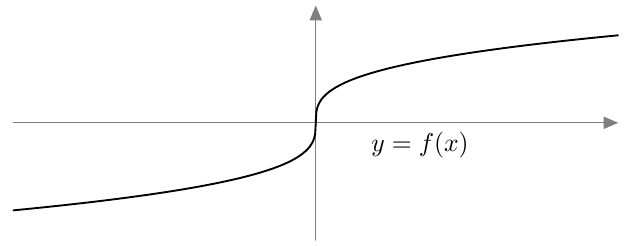
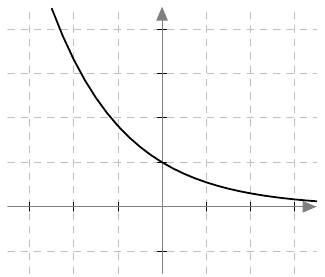
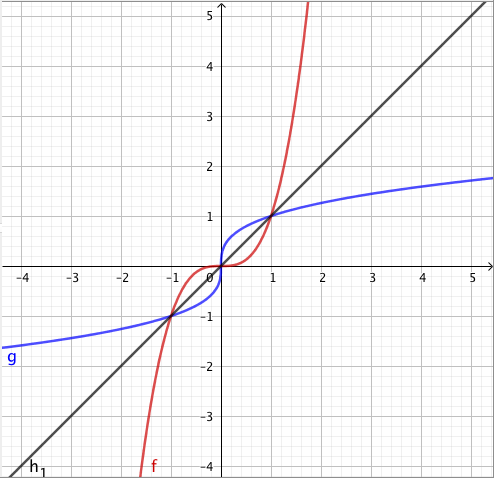
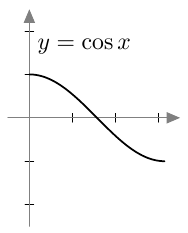
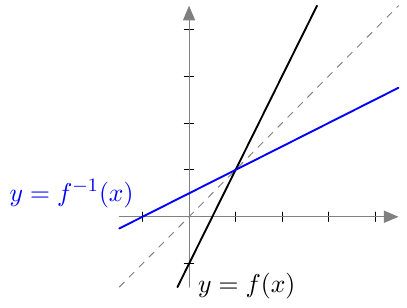
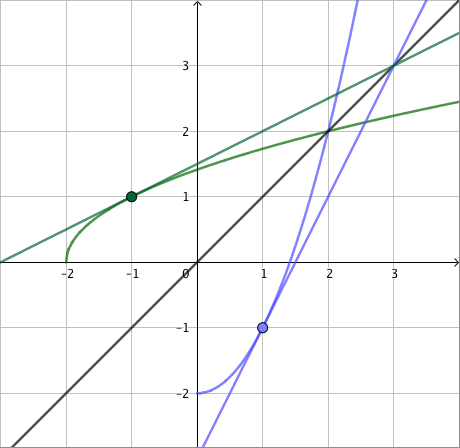
Jos yhtälössä esiintyy mikä tahansa parillinen juuri, valeratkaisut täytyy tunnistaa ja karsia pois samalla tavalla kuin neliöjuuren tapauksessa tehtiin. Tämä johtuu siitä, että parilliset potenssifunktiot saavat kaikki positiiviset arvonsa kahdessa eri kohdassa. Esimerkiksi alla olevasta neljännen asteen potenssifunktion kuvaajasta nähdään, että $$ x = \sqrt[4]{2} \Rightarrow x^4 = 2 $$ mutta $$ x^4 = 2 \Rightarrow x = \sqrt[4]{2} \ \text{ tai } \ x = -\sqrt[4]{2}. $$ 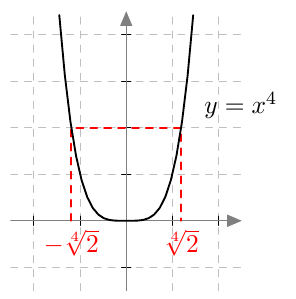
Parilliseen potenssiin korotusta ei siis voi kumota niin, että tuloksena olisi varmasti sama yhtälö mistä lähdettiin.
Ratkaise seuraava yhtälöt:
- $\sqrt[3]{x + 6} + 2 = 0$
- $\sqrt[3]{2x^3 + x} = 3x$
- $\sqrt{2-x} = \sqrt[4]{x}$
Vinkki: a-kohdassa muokkaa yhtälöä ennen potenssiin korotusta niin, että kuutiojuuren sisältävä termi on yksinään yhtälön toisella puolella.
- $x = -14$
- $x = 0$ tai $x = -\dfrac{1}{5}$ tai $x = \dfrac{1}{5}$
- $x = 1$
(Toinen ratkaisuehdokas $x = 4$ ei toteuta alkuperäisen yhtälön määrittelyehtoa.)